Príklady 2.kola zimnej časti 19.ročníka KSP-Z

Milé deti,

prikosnilo sa! A ešte len uvidíte, ako bude, keď sa tetka Perinbabka potkne a na svoju perinu spadne...

Preto sa uvelebte do postele, prikryte sa perinou a vezmite si tieto zadania KSP do ruky. Keď vás začne omíňať ľavý bok, ľahnite si na pravý.

Svoje riešenia nám posielajte do 17. decembra, a nezabudnite priložiť známky v hodnote 15 Sk,-.

• Zľabdaní zlatokopi
• Z trpaslíčich pretekov
• Záhada Jožkovej kalkulačky
• Zimbabwejské obchodné centrum
• Ziege Otto

Na Vyšnej Klondike sa začalo stavať nové mesto - New Očová. Urbanizačnú komisiu práve čaká ťažká úloha: musí rozhodnúť, ktoré stavebné parcely budú obývať zlatokopi a na ktorých sa postavia krčmy. Rozhodnúť však nemôže hocijako. Každý zlatokop chce mať krčmu nablízku. Preto parcela, na ktorej býva, musí susediť s nejakou parcelou, na ktorej je krčma. Naopak, nikto by nechcel vlastniť krčmu, pri ktorej nik nebýva. Každá krčma teda musí susediť s nejakou parcelou, na ktorej býva zlatopkop. Pomôžte urbanizačnej komisii a napíšte program, ktorý túto ťažkú ulohu vyrieši namiesto nich.

Úloha

Napíšte program, ktorý načíta N - počet parciel a M - počet dvojích parciel, ktoré spolu susedia. Program ďalej načíta M dvojíc čísel. Tieto dvojice určujú, ktoré parcely spolu susedia. Úlohou programu je vypísať, na ktorej parcele postaviť krčmu a ktorú majú obývať zlatokopi, aby pri tom boli splnené vyššie uvedené podmienky.

Príklad

Vstup
N=8, M=11

1 2         3 5
1 6         4 5
1 7         6 7
2 3         6 8
2 4         7 8
3 4

Výstup
Parcela č. 1 - stojí na nej krčma.
Parcela č. 2 - stojí na nej krčma.
Parcela č. 3 - obývaná zlatokopmi.
Parcela č. 4 - obývaná zlatokopmi.
Parcela č. 5 - stojí na nej krčma.
Parcela č. 6 - obývaná zlatokopmi.
Parcela č. 7 - obývaná zlatokopmi.
Parcela č. 8 - stojí na nej krčma.

Kde bolo, tam bolo, bolo raz jedno kráľovstvo. Konvexné kráľovstvo to bolo, a žili v ňom - no predsa trpaslíci. Každoročne tu prebiehala súťaž o najkonvexnejšo-konkávnejší rad trpaslíkov. Konkurencia je veľká, takmer všetky trpaslíčie rodinky chcú vyhrať, alebo sa aspoň zúčastniť. Koľkože problémov to však spôsobí odbornej kráľovskej porote, ktorá musí každý rad trpaslíkov pozorne preskúmať a určiť správnu konvexnosť a konkávnosť tohto radu...

Úloha

Kráľovská porota vás preto požiadala o pomoc; napíšte jej program, ktorý na vstupe dostane výšky trpaslíkov v rade a určí konvexnosť a konkávnosť tohto radu. Konvexnosť radu je dĺžka najdlhšieho konvexného úseku trpaslíkov; úsek trpaslíkov (i,j) s výškami a_i, a_i+1, ..., a_j-1, a_j nazývame konvexný, ak pre každých dvoch trpaslíkov z tohto úseku platí, že ak na hlavy týchto dvoch trpaslíkov položíme dosku, budú hlavy trpaslíkov medzi nimi nižšie ako doska. Konkávnosť radu definujeme podobne, pričom úsek trpaslíkov bude konkávny, ak všetci trpaslíci medzi vybranými dvoma budú vyšší ako doska. Keď nejaký úsek radu nie je konvexný, neznamená to ešte, že musí byť konkávny!

Príklad

Vstup
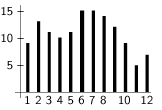
N = 12
9 13 11 10 11 15 15 14 12 9 5 7

Výstup
Konvexnosť: 5 (úsek 2-6)
Konkávnosť: 7 (úsek 5-11)

Jožko sa práve vrátil domov zo školy a chce sa ísť hrať von. Ale tak, ako všetky školopovinné deti, musí si aj on najprv napísať domácu úlohu. Zobral teda zošit z matematiky a začal čítať, čo sa vlastne učili. Zistil, že dnes sa v škole učili, ako sa počíta N!!! (pre tých, čo sa to ešte neučili: 0!!!=1, 1!!!=1, 2!!!=2. Ak N>=3, N!!! = N.(N-3)!!!; je to teda niečo ako faktoriál, ale berie sa každé tretie). No a teraz má z toho úlohu. Na takéto zákerné príklady má našťastie perfektnú kalkulačku s mnohými funkciami. Jednou z jej schopností je počítať veľmi presne aj s veľkými číslami. Začal teda počítať. Ale čoskoro s hrôzou zistil, že kalkulačka sa mu pokazila. Z akýchsi neznámych príčin okrem ľavostranných bezvýznamných núl vynecháva aj pravostranné významné nuly (napr. namiesto 1430000 zobrazí len 143). Našťastie si všimol, že má na stole ešte aj počítač, ktorý síce s veľkými číslami počítať nevie, ale dá sa na to naprogramovať. Ale to sa ešte v škole neučili a tak potrebuje vašu pomoc. Keďže kalkulačka mu ešte ako-tak funguje, stačí mu, ak zistíte, koľko núl musí dopísať k výsledku, ktorý mu vypíše kalkulačka.

Úloha

Je dané prirodzené číslo N. Zistite, koľkými nulami sa končí zápis čísla N!!! (v desiatkovej sústave).

Príklad

Vstup
N=47

Výstup
3
(47!!! = 262134882788466688000)

Najväčšia zimbabwejská spoločnosť Zima s.r.o. (s.r.o. = sneh radšej obmedzíme) sa rozhodla postaviť v Harare Zimbabwejské obchodné centrum. Architektúru budovy mal na starosti preslávený zimbabwejský architekt Mbwana. Jeho dovtedy najslávnejšia stavba bola metrová veža z kociek, ktorú postavil ako jedenásťročný. Teraz sa však rozhodol, že vykročí zo svojho tieňa a postaví stavbu ešte mohutnejšiu. Zachoval si však štýl - nová budova bude mať výšku H metrov a bude sa skladať z K kociek s celočíselnými dĺžkami hrán.

Aby však bola stavba bezpečná (čiže aby bola čo najmenšia šanca, že ju trafí lietadlo), musí mať čo najmenší objem. Tento problém Mbwana vyriešil šikovne - zadal ho preslávenému zimbabwejskému matematikovi Bwangovi. Bwang sa už preslávil napríklad tým, že spočítal všetky tri cesty, vedúce do Harare, ale táto úloha sa zdá byť nad jeho sily. Preto sa rozhodol požiadať vás o pomoc.

Úloha

Napíšte program, ktorý načíta výšku budovy H, počet kociek N <=H a vypíše dĺžky hrán N kociek takých, že keď tieto kocky postavíme na seba, dostaneme vežu výšky H s minimálnym možným objemom.

Príklad

Vstup
H=6, N=4

Výstup
2, 1, 2, 1
(celkový objem je 18)

Otto Ziege bol počas prvej svetovej vojny anglickým špiónom v Nemecku. V tých dobách bola ešte kryptografia v plienkach a neexistovali ešte žiadne šifry, tak ako ich poznáme dnes.

Raz sa mu podarilo zachytiť nasledujúcu tajnú správu:

e	s	b	m	t	o	k	y	i	n
v	ú	a	s	a	u	l	ť	s	ú
b	p	e	j	e	w	ch	e	s	k
e	d	z	e	e	n	e	a	m	č
ď	k	ň	z	i	a	l	n	s	z
a	n	o	ý	i	p	m	p	o	a
v	ľ	ý	o	k	m	n	a	o	l
e	d	h	n	e	a	r	a	l	r
i	o	s	l	o	á	o	p	z	o
v	y	i	m	d	á	p	b	r	s

 

Vedel, že správa musí obsahovať tieto slová: keď, úspech, podarilo, zimbabwe. Navyše vedel, že správa je šifrovaná nasledovným systémom: (Takéto informácie špióni mávajú)

Zoberieme štvorčekový papier a vystrihneme z neho štvorec 10x10 štvorčekov. Vhodnú štvrtinu (t.j. 25) štvorčekov vystrihneme. Vznikne nám šifrovacia mriežka. Položíme ju na papier a vpisujeme zľava doprava, zhora nadol do vystrihnutých okienok text, ktorý chceme zašifrovať, pričom vpisujeme do každého okienka práve jedno písmenko. Medzery a interpunkčné znamienka v texte sa preskakujú. Potom mriežku otočíme o 90^O stupňov v smere hodinových ručiek a postup opakujeme. Takto po 3 otočeniach máme vyplnený štvorec písmen 10x10. Samozrejme, že treba vedieť, ktoré štvočeky vystrihnúť, aby sa nám nestalo, že by sme do nejakého okienka nemohli zapísať písmenko. (Zamyslite sa, kedy to môže fungovať)

Ukážte, že nie ste o nič horší ako Otto a dešifrujte túto správu!

---

(c) 15. Novembra 2001 webmaster