Milé naše riešiteľky, milí naši riešitelia,
Dostali sa Vám do rúk ďalšie zadania KSP. Sú plné príkladov a preto neváhajte, ovtorte ich, prečítajte si ich a vyriešte ich (a samozrejme pošlite).
Termín odoslania riešení tejto série je streda 7. januára 2009.
Kto druhému jamu kope, nech sa do nej aj zasadí.
1. Zn. Kravina
10 bodov, kategória: Z
Vítame Vás v dnešnej KSPoradni. Hneď na úvod vyberáme z listárne tento príbeh:
Milí KSPáci. Pôjdem rovno k veci. Je to prekliatie a vy ste jediní kto mi môže
pomôcť. Už dva roky som sa poriadne nevyspal! Aby ste boli v obraze, tu je
názorná ukážka toho, čo sa deje každý večer, akonáhle zaspím.
Idem cez most. Je to celkom obyčajný most, preklenujúci celkom obyčajnú riečku. Aj nebo je obyčajné, a ani ten oblak v tvare dvojitého integrálu nie je ničím zvláštny. Odrazu vidím, že cez most ide oproti mne krava. "Ahoj krava," slušne pozdravím, tak, ako ma to doma učili. Krava ide pomaly, pretože nesie veľký elektrický ventilátor. Spýta sa ma, či by som ho nechcel lacno kúpiť. Hovorím jej, že nemám peniaze. "Dobre fafrnok, vymením ho za kliešte na šalát a pár ďalších vecí," odpovedá krava a vedno kráčame ku mne domov. "Ale rýchlo," dodá krava, a už obaja stojíme nad dlhým zoznamom náradia, ktorý mám vyvesený v dielni. Aby ste vedeli, mám v dielni asi 500 (16.60 EUR) druhov klieští, a naozaj si nepamätám, či kliešte na šalát medzi nimi sú. Na to mám ten zoznam. V ňom mám pekne v abecednom poradí vymenované všetko náradie aké som kedy v dielni mal a pri každom náradí mám zapísané číslo poličky, kde ho nájdem (prípadne, že ho už nemám). Zoznam je však hróózne dlhý, a krava sa hróózne ponáhľa na futbal, takže jej nikdy nestihnem nájsť ani tie kliešte a k zvyšku sa ani nedostaneme. Vždy keď som v hľadaní niekde medzi hrabľou na sneh a nožničkami na fikus, krava sa otočí na kopyte a povie, "Stretneme sa zajtra, zabudla som si doma tretry," a ja sa v tom momente zobudím a zvyšok noci neviem zaspať. A na druhý deň sa skutočne s kravou znova stretnem. Ach KSPáci, naprogramujte mi prosím program, ktorým by som svoj zoznam náradia dokázal fakt rýchlo prehľadať a tým uspokojiť tú kravu, čo mi robí zo života peklo.
Úloha
Na vstupe je na prvom riadku číslo  . Nasleduje
. Nasleduje  riadkov
popisujúcich náradie v dielni, pričom tieto riadky sú usporiadané vzostupne
podľa názvu náradia. Na
riadkov
popisujúcich náradie v dielni, pričom tieto riadky sú usporiadané vzostupne
podľa názvu náradia. Na  -tom riadku sa nachádza záznam o
-tom riadku sa nachádza záznam o  -tom náradí v
tvare názov náradia, medzera, číslo poličky. Ak sa náradie už v sklade
nenachádza, číslo poličky je
-tom náradí v
tvare názov náradia, medzera, číslo poličky. Ak sa náradie už v sklade
nenachádza, číslo poličky je 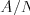 . Na vstupe nasleduje číslo
. Na vstupe nasleduje číslo  , označujúce
počet predmetov, ktoré krava chce výmenou za ventilátor. Každý z nasledujúcich
, označujúce
počet predmetov, ktoré krava chce výmenou za ventilátor. Každý z nasledujúcich
 riadkov popisuje jednu požiadavku kravy. Vašou úlohou je pre daný zoznam
náradia a dané požiadavky kravy v čo najrýchlejšom čase nejakým vhodným spôsobom
odpovedať, či dokážeme, alebo nedokážeme krave vyhovieť vo všetkých jej
požiadavkách.
riadkov popisuje jednu požiadavku kravy. Vašou úlohou je pre daný zoznam
náradia a dané požiadavky kravy v čo najrýchlejšom čase nejakým vhodným spôsobom
odpovedať, či dokážeme, alebo nedokážeme krave vyhovieť vo všetkých jej
požiadavkách.
V tejto úlohe nás zaujíma najmä to, ako efektívne rozhodujete o splniteľnosti požiadaviek. Preto budeme hodnotiť len úlohu, v ktorej predpokladáme, že máte zoznam náradia už načítaný v poli v takom poradí ako je na vstupe a vy už len idete odpovedať na kravine požiadavky. V programe samozrejme vstup do nejakého poľa načítať musíte. My túto fázu ale nebudeme zahŕňať do posudzovania efektívnosti vášho programu.
Príklad
Vstup
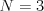
Fujara 733
Kefa na koňa 47
Kliešte na šalát 550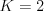
Kliešte na šalát
Fujara
Výstup
Dokážeme krave vyhovieť.
2. Zákerná hra
10 bodov, kategória: Z
Všetci si ju chcú zahrať. Je známa, je úžasná, je to Hra s veľkým H. A jej
pravidlá sú jednoduché. Na začiatku sa zoberú kartičky s náhodnými celými
číslami. Tie sa potom usporiadajú do postupnosti a hra môže začať. Hráči do nej
prichádzajú a odchádzajú z nej ako sa im páči. Avšak po tom, ako hráč z hry
odíde, už sa do nej nesmie znovu vrátiť.
Samotná hra spočíva v tom, že sa postupne odkrývajú kartičky. Pred odkrytím ľubovolnej karty sa môže každý hráč rozhodnúť, či hru opustí a taktiež každý prizerajúci sa môže rozhodnúť, či do nej vstúpi. Potom si všetci hráči, ktorí sú práve v hre, pripíšu toľko bodov, koľko je na karte, ktorá sa obrátila. Nakoniec vyhráva ten, koho počet bodov plus počet ťahov v hre dáva čo najväčšie číslo.
Marianna je v tejto hre dobrá, ale vždy hrá len intuitívne a nikdy potom nevie, či nemohla predsalen hrať lepšie. Preto vás poprosila, aby ste jej pomohli. Zapísala si celú postupnosť kariet z jej poslednej vyhratej hry a chcela by vedieť, počas otáčania ktorých kariet mala byť v hre, aby hrala optimálne.
Úloha
Napíšte program, ktorý dostane na vstupe číslo  a postupnosť celých čísel dĺžky
a postupnosť celých čísel dĺžky  a ako výstup vypíše súvislú podpostupnosť takú, že súčet jej prvkov a dĺžky je najväčší
možný.
a ako výstup vypíše súvislú podpostupnosť takú, že súčet jej prvkov a dĺžky je najväčší
možný.
Príklad
Vstup
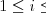
2 4 -1 6 -10 -12 2 10
Výstup
2 4 -1 6
Poznámka
(Marianna získa 15 bodov)
3. Zimomravý obdĺžnik
10 bodov, kategória: Z
Kedysi dávno v praveku bola príšerná zima. Prežili iba tie najschopnejšie tvory,
ktoré sa vedeli prispôsobiť. Ľudia lovili mamuty (Vraj tupými kopijami),
aby si mohli obliecť ich kožuchy. Mamuty lovili ľudí, aby ľudia nelovili
ich (Mamuty lovili všetkých, ktorí nelovili sami seba). Dinosaury
vyhynuli, lebo sa nevedeli obliecť. Náš obdĺžnik Maty sa tiež chce prispôsobiť.
V záujme straty čo najmenšieho množstva tepla chce mať čo najmenší obvod. Obsah
má ale nemenný ( palcov štvorcových) a má len celočíselné rozmery.
palcov štvorcových) a má len celočíselné rozmery.
Úloha
Vypíšte najmenší možný obvod obdĺžnika s celočíselnými rozmermi s daným obsahom  .
.
Príklad
Vstup
21
Výstup
20
Poznámka
rozmery 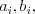
4. Zúfalý Miško
15 bodov, kategória: Z a O
Nie tak dávno náš kamarát Miško oslavoval meniny. Keďže má v obľube matematiku,
rodičia mu k meninám darovali novú grafickú kalkulačku TI-89 (TI-2.95EUR).
Poznáte ten pocit, keď dostanete úžasný darček a najradšej by ste ho ukázali
každému na svete? Presne toto urobil aj Miško a so svojou kalkulačkou sa
predvádzal pred všetkými v triede. Miška však napadlo, že o niekoľko dní bude
mať narodeniny jeho kamarátka, ktorá sa mu tak veľmi páči, takže by ju chcel
potešiť pekným darčekom. Ale nie a nie si spomenúť na ten osudový dátum, kedy
prišlo na svet to roztomilé a nádherné dievča... 20-teho? ... alebo
23-tieho? ... alebo 28-meho? Išiel teda po radu ku kamarátke Aničke, ktorá
samozrejme ako vždy všetko vedela. Ale Anička mu odpovedala takto: "Keďže máš
novú kalkulačku a toľko sa s ňou chváliš, budeš si to musieť vypočítať!" Tvoja
milovaná má narodeniny 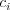 -teho októbra, kde
-teho októbra, kde  je 999-ta číslica zľava v
reťazci, ktorý dostaneme postupným písaním tretích mocnín prirodzených čísel za
sebou (bez medzier).
je 999-ta číslica zľava v
reťazci, ktorý dostaneme postupným písaním tretích mocnín prirodzených čísel za
sebou (bez medzier).
Úloha
Pomôžte Miškovi vypočítať presný dátum narodenín jeho tajnej lásky.
Napíšte program, ktorý na vstupe načíta prirodzené číslo  .
Na výstup vypíše (20+
.
Na výstup vypíše (20+ ), kde
), kde  je
je  -tá číslica v reťazci,
ktorý vznikne postupným písaním tretích mocnín všetkých prirodzených čísel (čize
-tá číslica v reťazci,
ktorý vznikne postupným písaním tretích mocnín všetkých prirodzených čísel (čize 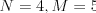 ).
).
Príklad
Vstup
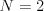
Výstup
2
Poznámka
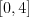
5. Obchodné orákulum
15 bodov, kategória: Z a O
Maják je veľmi dobrý burzový maklér. Dokázal zo-47-násobiť svoj majetok behom
jednej minúty (a behom ďalšej o väčšinu prišiel, ale to už je obchod). Za svoje
(ne)úspechy vďačí svojej poverčivosti. Naposledy od svojej osobnej veštice
kúpil skvelé obchodné orákulum. Obchodné orákulum vyzerá ako obyčajná
krištáľová guľa, avšak nie je v nej nič vidieť. Namiesto toto divne škvrčí a vylieza z
nej veľmi dlhý a tenký kus papiera popísaný všakovakými číslami.
Majákovi sa po čase podarilo rozlúštiť, čo to za čísla na tom papieri sú. Čísla
tvoria vývoj bankových úrokov v rôznych typoch bankových produktov na
najbližších pár dní. Ako vyzerá taký bankový produkt? Na  -ty bankový
produkt sa dajú uložiť peniaze v čase
-ty bankový
produkt sa dajú uložiť peniaze v čase 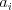 a v čase
a v čase 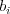 sa z neho musia
peniaze vybrať s tým, že budú zúročené o
sa z neho musia
peniaze vybrať s tým, že budú zúročené o 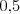 percent. Maják z~orákula dostal
popis
percent. Maják z~orákula dostal
popis  bankových produktov na najbližších pár dní a rozhodol sa, že svojich
bankových produktov na najbližších pár dní a rozhodol sa, že svojich
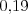 peňazí rozmnoží čo najviac, ako to pôjde. Na to ale bude potrebovať Vašu pomoc.
peňazí rozmnoží čo najviac, ako to pôjde. Na to ale bude potrebovať Vašu pomoc.
Úloha
Na prvom riadku vstupu budete mať čísla  ,
, 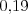 ,
, 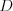 . Potom bude nasledovať
. Potom bude nasledovať
 riadkov s číslami
riadkov s číslami 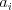 ,
, 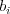 ,
, 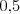 (
(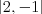 ,
,  ),
kde
),
kde 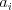 je čas, kedy sa dajú uložiť peniaze,
je čas, kedy sa dajú uložiť peniaze, 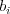 je čas, kedy je treba
vybrať peniaze a
je čas, kedy je treba
vybrať peniaze a 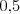 je úrok v percentách. Maják môže na ľubovoný produkt
uložiť koľko chce peňazí (samozrejme nie viac, ako aktuálne má). Vypočítajte,
koľko najviac peňazí vie mať Maják po
je úrok v percentách. Maják môže na ľubovoný produkt
uložiť koľko chce peňazí (samozrejme nie viac, ako aktuálne má). Vypočítajte,
koľko najviac peňazí vie mať Maják po 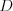 dňoch. Predpokladajte, že
dňoch. Predpokladajte, že 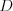 je
rádovo v tisícoch (
je
rádovo v tisícoch (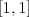 ), ale
), ale  môže byť veľmi veľké.
môže byť veľmi veľké.
Príklad
Vstup
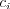 ,
, 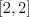 ,
, 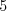
3 10 10
2 15 20
12 90 74
20 80 10
Výstup
191.4
6. On snáď nepozná žiadne zábrany!
20 bodov, kategória: O
Senzácia! Svetoznámy kryptológ Zemčo znova zabodoval! Jeho tretia kniha o mumifikovaných mačkách
láme všetky rekordy tržieb! Redakcii Klebetného Sobotného Plátku (KSP) sa s ním podarilo stretnúť, a
preto vám ako prví prinášame exkluzívne informácie. Zemčo nám v rozhovore prezradil, že kľúčom k jeho
úspechu je jeho podpisovanie kníh. Snaží sa, aby každý jeho podpis bol unikátny, čo zvyšuje
zberateľskú hodnotu. Podpisuje sa len číslami, vždy ich je niekoľko, a väčšie nasleduje za menším. A
aby si nemusel pamatäť, ktorý podpis už použil, tak si na ich vytváranie urobil počítačový program,
čo len svedčí o jeho neuveriteľnej všestrannosti. Fotku diskety, na ktorej sa tento program
nachádza, nájdete na druhej strane našej novej sobotnej prílohy "Čo ste vždy chceli vedieť o Pascale, ale báli
ste sa opýtať".
Úloha
Na vstupe sú dané dve prirodzené čísla  a
a  . Vašou úlohou je napísať program, ktorý vypíše
náhodnú
. Vašou úlohou je napísať program, ktorý vypíše
náhodnú  -prvkovovú rastúcu postuponosť čísiel z intervalu
-prvkovovú rastúcu postuponosť čísiel z intervalu  až
až 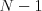 .
Program musí vrátiť naozaj náhodnú postupnosť, čo znamená, že každá z tých, ktoré prichádzajú do
úvahy ako možný výsledok, musí byť vygenerovaná s rovnakou pravdepodobnosťou. (Laicky
povedané, keby sme váš program spustili veľa krát, tak každá postupnosť by sa na výstupe objavila
približne rovnako veľa krát). Pri riešní úlohy môžete predpokladať, že máte k dispozícii funkciu
random(
.
Program musí vrátiť naozaj náhodnú postupnosť, čo znamená, že každá z tých, ktoré prichádzajú do
úvahy ako možný výsledok, musí byť vygenerovaná s rovnakou pravdepodobnosťou. (Laicky
povedané, keby sme váš program spustili veľa krát, tak každá postupnosť by sa na výstupe objavila
približne rovnako veľa krát). Pri riešní úlohy môžete predpokladať, že máte k dispozícii funkciu
random( ), ktorá vám vráti náhodné celé číslo z intervalu
), ktorá vám vráti náhodné celé číslo z intervalu  až
až  .
.
Príklad
Vstup
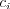 ,
, 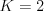
Výstup
0 3
7. O Holubej Pošte
20 bodov, kategória: O
Teploty na Kamčatke bežne klesajú hlboko pod nula (0.00~EUR) stupňov, čo
spôsobuje nemalé problémy miestnym obyvateľom. Jedna z postihnutých oblastí
je aj sektor telekomunikácií. Štandardné technológie sa nedajú použiť, keďže
zakopať káble do večne zamrznutej pôdy je takmer nemožné a nechať ich len tak
na povrchu zase veľmi riskantné berúc v úvahu zlú finančnú situáciu miestnych
obyvateľov. A na hocičo mobilné či satelitné tam aj tak nikto nemá peniaze.
Preto na Kamčatke, ako na jednom z mála miest na svete, ešte stále fungujú a aj
celkom profitujú storočiami (3.32~EURočiami) ošľahané technológie HP
(Holubia Pošta). Na službu v týchto nehostinných podmienkach sa používa
špeciálny, už niekoľko desiatok (0.33~EURok) generácií šľachtený, druh holuba.
Jeden z ostrieľaných hráčov na miestnom trhu je aj Prvá (0.03~EURtá) Kamčatská Súkromná Pošta (KSP), ktorá chystá novú super výhodnú službu. Stále ale ešte potrebuje dopočítať konkrétne detaily.
Kamčatka je dlhý a úzky poloostrov a pre jednoduchosť uvažujeme, že všetky mestá
ležia na jednej (0.03~EURej) priamke. Nová služba KSP spočíva v rozdelení všetkých
 miest na Kamčatke do
miest na Kamčatke do  skupín a poskytovaní veľmi výhodných mesačných
tarifných podmienok pre každú jednu (0.03~EUR) celú skupinu. Pre každú skupinu si vieme
porátať priemernú vzdialenosť medzi mestami. My chceme minimalizovať najväčšiu
priemernú vzdialenosť, aby žiaden holub nemusel naraz v priemere letieť príliš
ďaleko.
skupín a poskytovaní veľmi výhodných mesačných
tarifných podmienok pre každú jednu (0.03~EUR) celú skupinu. Pre každú skupinu si vieme
porátať priemernú vzdialenosť medzi mestami. My chceme minimalizovať najväčšiu
priemernú vzdialenosť, aby žiaden holub nemusel naraz v priemere letieť príliš
ďaleko.
Úloha
Dané je  ,
,  a
a  reálnych čísel
reálnych čísel 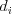 (
(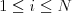 ) kde
) kde 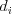 uvádza
vzdialenosť
uvádza
vzdialenosť  -teho mesta od Mysu Lopatka (Najjužnejší bod Kamčatky).
Nájdite najmenšie číslo
-teho mesta od Mysu Lopatka (Najjužnejší bod Kamčatky).
Nájdite najmenšie číslo 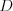 také, že je možné rozdeliť
také, že je možné rozdeliť  miest do
miest do  skupín tak,
že priemerná vzdialenosť miest v žiadnej skupine nie ja väčšia ako
skupín tak,
že priemerná vzdialenosť miest v žiadnej skupine nie ja väčšia ako 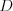 .
.
Príklad
Vstup
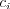 ,
, 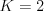
Vzdialenosti: 1 7 2 9
Výstup
2
Poznámka
Optimálne riešenie je mať prvé a tretie mesto v jednej a druhé a štvrté mesto v druhej skupine.
8. Ohrozené druhy
25 bodov, kategória: O a T
Súostrovie Kiribati bývalo voľakedy plné ohrozených druhov. Dnes je súostrovie Kiribati plné
vyhynutých druhov. Multimilionár (multi-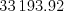 ~EUR-onár) Hermi von Lamač tam kúpil za babku
(0.03~EURobabky) jeden zveroprázdny ostrov a rozhodol sa postaviť tam brutálne luxusný hotel.
~EUR-onár) Hermi von Lamač tam kúpil za babku
(0.03~EURobabky) jeden zveroprázdny ostrov a rozhodol sa postaviť tam brutálne luxusný hotel.
A v tomto okamihu prichádzajú do hry Grínpisáci (Od anglického "green piss".). A keď vravíme "do hry", myslíme tým priamo za Hermim. S návrhom, ktorý sa nedá odmietnuť. Ževraj čím viac nových zvierat dá vypustiť do voľnej prírody, tým menej protestov a sabotáží bude mať pri výstavbe hotelu. No nekúp to. Ale Hermi je oddávna líška prešibaná. Rozhodol sa on, že Grínpisákov prešt... ehm, chceme povedať prekabáti. Zvieratká, ktoré dá vypustiť, budú všežravce ohavné.
Lenže keď už malo prísť k vypusteniu, uvedomil si Hermi jeden závažný nedostatok svojho plánu. Rozhodne nechce dopustiť, aby sa nejaký všežravec mohol vyskytnúť na ostrove, kde má hotel!
Úloha
Kiribati sa skladá z  ostrovov, očíslovaných od 1 do
ostrovov, očíslovaných od 1 do  .
Na ostrove s číslom 1 bude stáť Hermiho hotel.
.
Na ostrove s číslom 1 bude stáť Hermiho hotel.
Existuje práve  dvojíc ostrovov, medzi ktorými je postavený most.
Mosty nikde netvoria cyklus (Nedá sa teda spraviť to, že začneme
na nejakom ostrove, prejdeme cez niekoľko mostov (cez každý most najviac raz)
a skončíme na ostrove, kde sme začínali.).
Všežravce sa normálne cez most chodiť boja. Ale keď sú na jednom ostrove dva všežravce,
môže jeden zožrať druhého, tým naberie odvahu, a následne môže prebehnúť cez jeden most.
dvojíc ostrovov, medzi ktorými je postavený most.
Mosty nikde netvoria cyklus (Nedá sa teda spraviť to, že začneme
na nejakom ostrove, prejdeme cez niekoľko mostov (cez každý most najviac raz)
a skončíme na ostrove, kde sme začínali.).
Všežravce sa normálne cez most chodiť boja. Ale keď sú na jednom ostrove dva všežravce,
môže jeden zožrať druhého, tým naberie odvahu, a následne môže prebehnúť cez jeden most.
Na vstupe sú dané čísla  ,
,  a pre každý z
a pre každý z  mostov čísla ostrovov, ktoré spája.
Hermi môže vypustiť zviera na ľubovoľnom ostrove. Zistite, koľko najviac
všežravcov môže dokopy Hermi vypustiť, ak ich optimálne rozmiestni.
(Pozor, môže sa stať, že odpoveď je "ľubovoľne veľa".)
mostov čísla ostrovov, ktoré spája.
Hermi môže vypustiť zviera na ľubovoľnom ostrove. Zistite, koľko najviac
všežravcov môže dokopy Hermi vypustiť, ak ich optimálne rozmiestni.
(Pozor, môže sa stať, že odpoveď je "ľubovoľne veľa".)
Príklad
Vstup
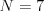 ,
, 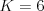
mosty: 1--2, 2--3, 3--4, 2--5, 1--6, 7--6.
Výstup
11
9. Túžba po rovnováhe
25 bodov, kategória: T
V tomto zadaní sa budeme venovať filozofickým úvaham na tému
rovnováha, pozitívne myslenie a emocionálne prežívanie života. Vďaka dlhoročnej
práci dokážu ľudia poodhaliť tajomstvá energie, ktorá spočíva
v rovnováhe ducha, tela a mysle a dosiahnúť tak dokonalú harmóniu.
Maroško sa po namáhavom štúdiu týchto vznešených teórií rozhodol, že svoj život usporiada tak, aby mu to prinieslo čo najviac blaha. Ba čo viac, usporiada život a vzťahy všetkým naokolo!
Ako správny praktický programátor ale Maroško vie, že život je otázka priorít. Preto si povedal, že dosiahne dokonalú rovnováhu a emocionálnu naplnenosť, zatiaľčo pozitívne myslenie odloží bokom na neskôr. Preto si stanovil nasledovné ciele:
- Každý vzťah v jeho okolí musí byť ladený alebo pozitívne, alebo negatívne. Neutrálny vzťah nemôže existovať, pretože by priniesol do života človeka nezdravú dávku fádnosti a stereotypu.
- Každý človek musí mať dokonale vybalancované negatívne a pozitívne myslenie. Existuje len jedna hodnota miery orientácie vzťahu, takže jeden ľubovoľný pozitívny a jeden ľubovoľný negatívny vzťah sa navzájom vyrovnajú. Inými slovami, každý človek musí mať rovnaký počet negatívnych a pozitívnych vzťahov.
Vzťah je orientovaný pre oboch zúčastnených ľudí rovnako -- alebo ho obaja vnímajú pozitívne, alebo ho obaja vnímajú negatívne (I keď autori ľúbostných piesni majú často opačné skúsenosti). Maroško teda stojí pred úlohou pre každý vzťah v jeho okolí určiť, či bude pozitívne alebo negatívne naladený. A keďže ľudí a vzťahov medzi nimi môže byť celkom požehnane, pomôžte mu a napíšte rýchly program, ktorý to urobí za neho!
Úloha
Na vstupe sú čísla  a
a  -- počet ľudí v Maroškovom okolí a počet vzťahov medzi nimi. Nasleduje
-- počet ľudí v Maroškovom okolí a počet vzťahov medzi nimi. Nasleduje
 dvojíc čísel ľudí, medzi ktorými existuje vzťah. Môžete predpokladať, že žiadna dvojica ľudí nie
je na vstupe uvedená viac ako raz. Pre danú spoločenskú sieť nájdite spôsob, ako nastaviť vzťahy
medzi ľuďmi. V prípade, že takéto nastavenie neexistuje, prehláste, že to nejde.
dvojíc čísel ľudí, medzi ktorými existuje vzťah. Môžete predpokladať, že žiadna dvojica ľudí nie
je na vstupe uvedená viac ako raz. Pre danú spoločenskú sieť nájdite spôsob, ako nastaviť vzťahy
medzi ľuďmi. V prípade, že takéto nastavenie neexistuje, prehláste, že to nejde.
Príklad
Vstup
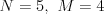
1 2
2 3
3 4
4 1
Výstup
1 2 - pozitivny
2 3 - negativny
3 4 - pozitivny
4 1 - negativny
Príklad
Vstup
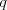
1 2
2 3
3 4
4 1
5 6
Výstup
V tomto svete nie je súdené dosianúť dokonalú harmóniu.
10. Trasa okolo rovníka
25 bodov, kategória: T
Hermi sa presťahoval na rovník. Spravil tak preto, lebo má na rovníku strašne
veľa kamarátov a nechce kaziť partiu. Teraz sa chce vydať na okružnú cestu okolo
Zeme, pričom bude letieť lietadlom a bude pristávať iba tam, kde má kamarátov.
Hermi pozná všetky obojsmerné linky, ktoré lietajú medzi jeho kamarátmi. Pre
jednoduchosť budeme polohy miest označovať uhlom medzi  a
a 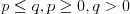 pričom uhol
rastie zo západu na východ. Každé lietadlo letí po najkratšej ceste medzi dvomi
miestami. To znamená, že ak lietadlo letí z pozície
pričom uhol
rastie zo západu na východ. Každé lietadlo letí po najkratšej ceste medzi dvomi
miestami. To znamená, že ak lietadlo letí z pozície 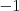 (11.61 EUR) do
(11.61 EUR) do 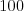 (3.31 EUR), bude letieť zo západu na východ (preletí
(3.31 EUR), bude letieť zo západu na východ (preletí 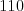 stupňov (3.65 EUR)). Môžete
predpokladať, že žiadna linka nebude spájať dve mestá, ktoré sa nachádzajú
presne oproti sebe.
stupňov (3.65 EUR)). Môžete
predpokladať, že žiadna linka nebude spájať dve mestá, ktoré sa nachádzajú
presne oproti sebe.
Hermi chce obletieť Zem. To znamená, že vzdialenosť, ktorú preletí zo západu na východ sa nesmie rovnať vzdialenosti, ktorú preletí z východu na západ. Chce, aby musel čo najmenej prestupovať a svoju cestu začína aj končí u svojho najlepšieho kamaráta.
Úloha
Na vstupe je najprv celé číslo  , udávajúce počet Hermiho kamarátov, a celé
číslo
, udávajúce počet Hermiho kamarátov, a celé
číslo  udávajúce počet obojsmerných liniek. Nasleduje
udávajúce počet obojsmerných liniek. Nasleduje  čísel
čísel 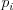 , ktoré
udávajú pozíciu kamarátov. Ďalej je na vstupe
, ktoré
udávajú pozíciu kamarátov. Ďalej je na vstupe  dvojíc
dvojíc 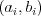 , ktoré
hovoria, že medzi kamarátmi číslo
, ktoré
hovoria, že medzi kamarátmi číslo 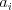 a
a 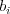 lieta obojsmerná linka. Hermiho
najlepší kamarát má číslo 1 (0.03 EUR). Vašou úlohou je zistiť, na koľko
najmenej letov vie Hermi obletieť Zem. Začať aj skončiť musí u svojho
najlepšieho kamaráta.
lieta obojsmerná linka. Hermiho
najlepší kamarát má číslo 1 (0.03 EUR). Vašou úlohou je zistiť, na koľko
najmenej letov vie Hermi obletieť Zem. Začať aj skončiť musí u svojho
najlepšieho kamaráta.
Príklad
Vstup
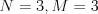
0 120 240
1 2
2 3
1 3
Výstup
3