Milé naše riešiteľky, milí naši riešitelia.
Opäť sa vám dostávajú do rúk zadania Vášho obľúbeného semináru a určite sa tešíte na riešenie skvelých príkladov. Aby ste náhodou nenadobudli pocit, že to robíte nadarmo, pripomíname Vám, že najlepších čaká pozvánka na sústredko, a tých najlepších z najlepších navyše aj úžasné knižné ceny. A pre víťaza kategórie T samozrejme okrem knižnej odmeny aj nehynúca sláva, a dav rozvášnených fanyniek (KSP neručí, za žiadnu súčasť ceny s výnimkou knižnej).
A dokedy toto všetko? Termín odoslania riešení tejto série je už pondelok 9. marca 2009.
Lenivec je ten, čo nerobí zbytočné pohyby.
1. Zabudnutý PIN
10 bodov, kategíria: Z
Etome je informatik a má zlú pamäť na čísla. Zato počítanie, to mu ide.
Vie napríklad z hlavy vypočítať ľubovoľný faktoriál. (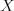 faktoriál,
značené
faktoriál,
značené 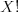 , je súčin čísel od 1 po
, je súčin čísel od 1 po 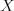 vrátane.)
vrátane.)
Táto jeho schopnosť má kopu praktických využití. Napríklad si takto pamätá
svoj päťmiestny PIN (Nie, nie je to preklep,
Etome naozaj používa päťmiestny PIN kód) -- miesto neho si pamätá len
číslo  a vie, že jeho PIN je tvorený poslednými piatimi
ciframi
a vie, že jeho PIN je tvorený poslednými piatimi
ciframi 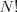 .
.
Počas minulého leta Etome brigádoval jedna radosť. Zo svojich prvých zarobených peňazí sa rozhodol kúpiť si televízor. Prišiel do miestneho obchodu s elektronikou, kde sa odohral nasledujúci rozhovor
-- Dobrý deň, máte prosím vás farebné televízory?
-- Máme.
-- Tak si prosím jeden zelený.
-- V poriadku, tie máme po štyristo. Budete platiť v hotovosti alebo kartou?
-- Kartou.
A tu nastal problém. Bohužiaľ, Etome bol zase do šiestej ráno hore a teraz mu to
rátanie z hlavy nejde až tak dobre.
Úloha
Dané je kladné celé číslo  . Pomôžte Etomovi a vypočítajte jeho PIN. Inými
slovami, vypočítajte posledných päť cifier čísla
. Pomôžte Etomovi a vypočítajte jeho PIN. Inými
slovami, vypočítajte posledných päť cifier čísla 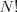 . (Ak má
. (Ak má 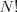 menej ako
5 cifier, vypíšte ich zľava doplnené nulami.)
menej ako
5 cifier, vypíšte ich zľava doplnené nulami.)
Keďže Etome môže v budúcnosti chcieť bezpečnejší PIN (primalé  by mohlo spôsobiť
bezpečnostné riziko), mal by váš program fungovať pre ľubovoľne veľké
by mohlo spôsobiť
bezpečnostné riziko), mal by váš program fungovať pre ľubovoľne veľké  ,
aké sa vám ešte zmestí do premennej.
,
aké sa vám ešte zmestí do premennej.
Príklad
Vstup
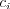
Výstup
00024
Vstup
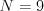
Výstup
62880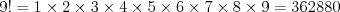
2. Zapichnutá hrana
10 bodov, kategória: Z
Traja prestarnutí dôchodcovia Miško, Kubko a Vladko, ktorých už pozeranie slovenského futbalu začalo nudiť, si na svojom fialovom televízore naladili najnovšiu argentínsku telenovelu. Zrovna fičal asi 507. diel. Situácia v telenovele sa začala prudko zamotávať. Každú polminútu sa objavil nový vzťah, takže bol z toho akurát pekný bordel. Nasledovala reklamná prestávka, počas ktorej sa odohral nasledujúci rozhovor
-- Vladko: "Tušíte vôbec, kto je hlavný hrdina?"
-- Kubko: "To bude tá Mária, tu chcú asi desiati..."
-- Miško: "Podľa mňa to bude zas tá Lucia, tá chcela asi štrnástich..."
-- Vladko: "Ehm ten, ako sa volá... Peter... toho chcelo asi dvanásť."
-- Kubko: "To si koho zarátal? Učili ťa na tom matfyze vôbec počítať?"
Ako vidíte, schyľuje sa k miernej hádke, takže vašou úlohou je porátať, kto je v danej telenovele
najväčšia ihelnička a kto najväčší ježko.
Úloha
Na vstupe je počet postáv  a počet vzťahov
a počet vzťahov  .
Postavy sú očíslované prirodzenými číslami od
.
Postavy sú očíslované prirodzenými číslami od 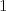 po
po  .
Nasleduje
.
Nasleduje  dvojíc čísel
dvojíc čísel 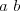 , pričom každá dvojica vyjadruje, že postava
, pričom každá dvojica vyjadruje, že postava  chce (Resp.
niekedy počas deja chcela) postavu
chce (Resp.
niekedy počas deja chcela) postavu  . Môžete predpokladať, že každá informácia sa na vstupe
vyskytne práve raz -- ale pozor, môže sa najprv vyskytnúť
najskôr dvojica
. Môžete predpokladať, že každá informácia sa na vstupe
vyskytne práve raz -- ale pozor, môže sa najprv vyskytnúť
najskôr dvojica 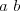 a potom aj
a potom aj 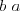 .
.
Vašou úlohou je vypísať dve čísla postáv -- číslo postavy, ktorú chce najviac iných (tzv. ihelnička) a číslo postavy, ktorá chce najviac iných (tzv. ježko). Zároveň zistite pre každého jeho stupeň -- počet postáv ktoré chcú ihelničku/chce ježko. Pokiaľ existuje viac správnych možností, vypíšte ľubovoľnú z nich.
Dôležité upozornenie: Nepredpokladajte nič o pohlaviach postáv zodpovedajúcich vstupu!
Príklad
Vstup
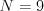 ,
, 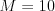
1 4
2 4
3 4
4 3
5 2
6 7
6 5
6 8
8 6
9 7
Výstup
Ihelnicka je: 4, stupen 3
Jezko je: 6, stupen 3
P.S.: Kto zistí, ktorí ľudia sa skrývajú za danými vrcholmi, má u U$Ámu kofolu :).
3. Zoltánove televízory
10 bodov, kategória: Z
Keď bol Malý Zoltán ešte malý, dostal na narodeniny takú skvelú stavebnicu. Skladala sa z tyčí a spojníc. Tyče boli rôznej dĺžky a spojnice boli také guličky, ktoré vedeli spojiť konce 1 až 5 tyčí. Malému Zoltánovi (V čase, keď bol ešte malý.) sa táto stavebnica veľmi páčila a denno-denne sa s ňou hrával.
Zoltán časom vyrástol, vyštudoval matfyz, založil si rodinu a mal syna Malého Zoltána mladšieho. Malý Zoltán mladší má momentálne svoje druhé narodeniny a tak dostal od Malého Zoltána jeho obľúbenú(Obľúbená bola v čase, keď bol ešte malý.) stavebnicu. Malý Zoltán mladší pri takom darčeku nadšene vykríkol a hneď sa začal so stavebnicou hrať. Keďže malý Zoltán mladší je ešte veľmi malý, tak to neskladal len tak s rozmyslom, ale len tak náhodne. Keď sa dohral, tak od vyčerpania zaspal.
Malý Zoltán uložil Malého Zoltána mladšieho spať a rozhodol sa to upratať. Pritom si všimol, že Malý Zoltán mladší postavil niekoľko televízorov. Tak si Malý Zoltán(Ako správny matfyzák...) prepísal popisy jednotlivých výtvorov do počítača a rozhodol sa, že si spraví program, ktorý mu zistí, ktoré z nich sú televízory.
Úloha
Prvý riadok vstupu obsahuje čísla  a
a  , kde
, kde  je počet spojovníkov
(spojovníky sú očíslované od
je počet spojovníkov
(spojovníky sú očíslované od 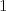 po
po  ) a
) a  je počet tyčí. Druhý riadok
vstupu obsahuje
je počet tyčí. Druhý riadok
vstupu obsahuje  čísiel
čísiel 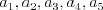 , pričom
, pričom 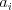 označuje
počet spojovníkov, ktoré spájajú práve
označuje
počet spojovníkov, ktoré spájajú práve  tyčí (Platí, že
tyčí (Platí, že 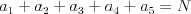 .)
Ďalej nasleduje
.)
Ďalej nasleduje  riadkov, pričom každý z nich obsahuje dve čísla
riadkov, pričom každý z nich obsahuje dve čísla  a
a  ,
ktoré hovoria, že medzi spojovníkmi
,
ktoré hovoria, že medzi spojovníkmi  a
a  vedie tyč.
vedie tyč.
Samozrejme medzi každou dvojicou spojovníkov môže viesť maximálne jedna tyč. Každá tyč má na každom svojom konci jeden spojovník. Navyše môžete predpokladať, že útvar popísaný vstupom programu "drží pokope" -- teda že by mravce vedeli preliezť z ľubovoľného miesta na ľubovoľné iné bez toho, aby museli opustiť povrch útvaru.
Ako spoznáme televízor? Televízor je "bedňa" s dvoma "anténami", ktoré
vychádzajú z toho istého miesta. Bedňu vyrobíme tak, že zoberieme niekoľko spojovníkov (aspoň
tri) a toľko isto tyčí a zapojíme ich do jedného veľkého kruhu -- teda z každého spojovníka povedú
práve dve tyče. Potom si vyberieme ľubovoľný
spojovník a pridáme mu dve (môžu byť aj rôzne dlhé) antény. Anténa je niekoľko (aspoň 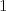 ) tyčí
pospájaných do radu za sebou.
) tyčí
pospájaných do radu za sebou.
Vašou úlohou je pre daný vstup povedať, či je daný kus stavebnice televízor alebo nie.
Príklad
Vstup
8 8
2 5 0 1 0
1 3
2 3
3 4
4 5
5 6
6 7
7 3
2 8
Výstup
Vstup je televizor.
Vstup
7 7
3 3 0 0 1
1 3
2 3
3 4
4 5
5 6
6 3
7 3
Výstup
Vstup nie je televizor.
(Lebo zo spojovníka 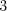 idú až 3 antény.)
idú až 3 antény.)
4. Obrazovka je na eskykráliky malá
15 bodov, kategória: Z a O
Ako iste všetci viete, na Sibíri bývajú Eskimáci a Eskimáčky. Po dlhšom pobyte sa dajú odpozorovať aj eskikocúry a rôzne iné zvery. Upriamme ale našu pozornosť na eskikráliky. Veľmi sa nelíšia od obyčajných králikov, žijú podobným životom až na dva rozdiely.
Prvý sa týka rozmnožovania. Naše slovenské králiky sa rozmnožujú podľa Fibonacciho postupnosti ( http://www.novinky.cz/clanek/109771-hrajeme-zdarma-fibonacci-chytejte-kraliky.html ). Ale eskikráliky to dokážu ešte rýchlejšie -- každú sekundu sa z jedného eskikrálika stanú dvaja~-- severný a južný. Líšia sa v tom, že severný skáče na sever a južný na juh. Každý eskikrálik spraví jeden skok za jednu sekundu a jeho skok má dĺžku presne jeden meter.
Druhý rozdiel sa týka stravy. Naše králiky sú vyberavé, nezožerú len tak hocičo. Zvykli si zväčša na mrkvu a iné obilniny. Eskikráliky žijú v drsnom prostredí, takže nie sú také chúlostivé. Uspokoja sa s hocičím, čo sa hýbe. Takže keď sa stretnú severný a južný králik, tak sa navzájom zožerú a nezostane z nich nič. Ak sa v jednom momente má králik aj rozmnožovať aj zjesť iného králika, prioritu má jedlo.
Na Sibíri bol na začiatku jeden králik. Odvtedy sa opakuje nasledovný kolobeh:
- Každý králik sa rozmnoží. Jeho severná verzia skočí na sever, južná verzia skočí na juh.
- Ak sú na nejakom mieste dva králiky, tak sa navzájom zožerú a nezostane z nich nič.
Novinári prišli na Sibír v čase  (keď ešte existival iba jeden králik) a hneď začali natáčať
dokumentárny film o králikoch. Snímky robili na začiatku každej sekundy (tesne pred rozmnožovaním).
Králikov však bolo časom tak veľa, že sa skoro nezmestili na obrazovku
televízora. Preto sa film dá pozerať len na najkvalitnejších 47-palcových HD
ready fialových televízoroch. Kameru novinári fialovú nemali, iba takú
nekvalitnú zelenú, preto im vypadol
(keď ešte existival iba jeden králik) a hneď začali natáčať
dokumentárny film o králikoch. Snímky robili na začiatku každej sekundy (tesne pred rozmnožovaním).
Králikov však bolo časom tak veľa, že sa skoro nezmestili na obrazovku
televízora. Preto sa film dá pozerať len na najkvalitnejších 47-palcových HD
ready fialových televízoroch. Kameru novinári fialovú nemali, iba takú
nekvalitnú zelenú, preto im vypadol  -tý obrázok. A práve ten bol dôležitý!
Preto sa obracajú na vás, programátorov, aby ste im zrekonštruovali situáciu v
-tý obrázok. A práve ten bol dôležitý!
Preto sa obracajú na vás, programátorov, aby ste im zrekonštruovali situáciu v
 -tej sekunde.
-tej sekunde.
Úloha
Na vstupe máte dané  -- sekunda, ktorú chceme zrekonštruovať. Výstupom majú
byť počty králikov na jednotlivých pozíciách od najjužnejšieho po
najsevernejšieho.
-- sekunda, ktorú chceme zrekonštruovať. Výstupom majú
byť počty králikov na jednotlivých pozíciách od najjužnejšieho po
najsevernejšieho.
Príklad
Vstup
2
Výstup
1 0 0 0 1
(V nultej sekunde je jeden eskikrálik. Potom sa rozmnoží, potomkovia bežia a v prvej sekunde sú dvaja na pozíciách 0 a 2. Potom sa rozmnožia, bežia, zožerú a v druhej sekunde sú tak ako vo výstupe (na fialovom televízore).)
5. Zlý príjem
15 bodov, kategória: Z a O
Nech nastavíte anténu na žltom televízore Merkur ako len chcete, akonáhle si sadnete do kresla, začne sa príjem postupne zhoršovať, až nakoniec dostanete len šum.
Kvalitu príjmu môžeme označiť číslom od 9 (skoro dokonalé) po 0 (samé zrno). Spravme teraz nasledovný experiment: Nastavíme anténu, sadneme do kresla a každých 5 minút zapíšeme kvalitu obrazu. Keď už zostane len zrnenie, experiment ukončíme. Môžeme takto dostať napríklad číslo 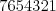 (obraz sa postupne zhoršoval),
(obraz sa postupne zhoršoval), 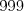 (štvrť hodiny to šlo, potom bum a zrazu nič) alebo
(štvrť hodiny to šlo, potom bum a zrazu nič) alebo 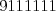 (chvíľku to šlo pekne, a potom ešte pol hodinky bolo vidieť obrysy postáv).
(chvíľku to šlo pekne, a potom ešte pol hodinky bolo vidieť obrysy postáv).
Čísla, ktoré môžeme pri experimente dostať, nazveme zrnité. Postupnosť všetkých zrnitých čísel (usporiadaných vzostupne podľa numerickej hodnoty) vyzerá nasledovne:
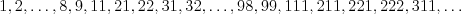
Zrnité číslo sa skladá z cifier  a jeho cifry tvoria nerastúcu
postupnosť (každá ďalšia cifra je buď rovnaká, alebo menšia ako predchádzajúca
cifra). Napríklad číslo
a jeho cifry tvoria nerastúcu
postupnosť (každá ďalšia cifra je buď rovnaká, alebo menšia ako predchádzajúca
cifra). Napríklad číslo 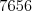 nie je zrnité, lebo po cifre
nie je zrnité, lebo po cifre  nasleduje cifra
nasleduje cifra
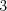 . Číslo
. Číslo 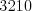 nie je zrnité preto, lebo obsahuje cifru
nie je zrnité preto, lebo obsahuje cifru  .
.
Úloha
Pre čo najviac 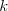 z množiny
z množiny  nájdite číslo, ktoré je v
postupnosti zrnitých čísel na mieste
nájdite číslo, ktoré je v
postupnosti zrnitých čísel na mieste 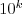 . Čím viac správnych čísel pošlete,
tým viac bodov dostanete. (Pošlite nám aj programy, pomocou ktorých ste tieto
čísla hľadali.)
. Čím viac správnych čísel pošlete,
tým viac bodov dostanete. (Pošlite nám aj programy, pomocou ktorých ste tieto
čísla hľadali.)
Príklad
Vstup
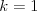
Výstup
Na pozícii 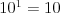 je číslo 11.
je číslo 11.
6. Obchod plný televízorov
20 bodov, kategória: O
Mladý Kleofáš dostal bojovú úlohu. Má vybrať pre rodinu nový televízor. Kleofáš dobre vie, že jeden z najdôležitejších parametrov je veľká uhlopriečka, a tak sa vybral do obchodu a hľadal televízor s tou najväčšou uhlopriečkou. Keďže Kleofáš ešte nevie čítať číslice, začal splašene pobehovať po obchode, porovnáva uhlopriečky dvojíc televízorov a zapisuje si výsledky. Teraz prišiel domov a snaží sa zostrojiť rebríček televízorov tak, aby nebol nejaký televízor pred iným, o ktorom vie, že má väčšiu uhlopriečku. Televízorov bolo obchode veľmi veľa, a preto bude potrebovať vašu pomoc.
Úloha
Napíšte program, ktorý na vstupe dostane čísla  a
a  , kde
, kde  je počet televízorov a
je počet televízorov a  je počet porovnaní. Za nimi bude nasledovať
je počet porovnaní. Za nimi bude nasledovať  dvojíc televízorov (Kleofáš nepoužíval
čísla, ale my si to uľahčíme a budeme televízory označovať číslami od
dvojíc televízorov (Kleofáš nepoužíval
čísla, ale my si to uľahčíme a budeme televízory označovať číslami od 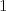 po
po  .)
.) 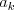
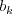 ,
ktoré hovoria o tom, že televízor
,
ktoré hovoria o tom, že televízor 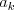 má väčšiu uhlopriečku ako
má väčšiu uhlopriečku ako 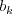 .
.
Vašou úlohou je zoradiť televízory do postupnosti 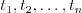 podľa
uhlopriečky tak, aby pre žiadne dva televízory
podľa
uhlopriečky tak, aby pre žiadne dva televízory 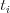 a
a 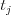 kde
kde 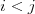 ,
neexistovalo porovnanie na Kleofášovom zozname, ktoré by hovorilo o tom, že
televízor
,
neexistovalo porovnanie na Kleofášovom zozname, ktoré by hovorilo o tom, že
televízor 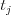 má väčšiu uhlopriečku ako televízor
má väčšiu uhlopriečku ako televízor 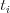 . Inak
povedané, každý televízor je v poradí pred všetkými televízormi o ktorých
vieme, že majú menšiu uhlopriečku.
. Inak
povedané, každý televízor je v poradí pred všetkými televízormi o ktorých
vieme, že majú menšiu uhlopriečku.
Príklad
Vstup
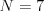 ,
, 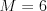
1 5
6 7
3 4
1 2
7 2
6 1
Výstup
3 4 6 7 1 5 2
(Všimnite si, že napríklad aj usporiadanie 6 1 3 7 5 4 2 je správne.)
7. Obchod s televízormi
20 bodov, kategória: O
Marek sa rozhodol, že skončí so školou a založí si obchod s modrými televízormi. Jeho obchod sa stal rýchlo veľmi populárnym najmä medzi študentmi, ktorí si nový televízor kupujú veľakrát do roka a väčšinou viacero naraz. Keďže ide o chudobných študentov, tak chcú kúpiť vždy televízory za najnižšiu možnú cenu. Navyše k Marekovi chodia občas dodávatelia, ktorí dovezú niekoľko rovnakých kusov televízorov. Pomôžte Marekovi, aby vedel prichádzajúcich zákazníkov obslúžiť čo najrýchlejšie.
Úloha
Prvý riadok obsahuje číslo  -- počet udalostí. Nasleduje zoznam
-- počet udalostí. Nasleduje zoznam  udalostí.
Každá udalosť môže byť dvoch typov: "1
udalostí.
Každá udalosť môže byť dvoch typov: "1 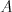
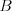 " alebo "2
" alebo "2 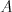 ". Všetky čísla sú
celé. Prvá udalosť je príchod dodávateľa, ktorý priniesol
". Všetky čísla sú
celé. Prvá udalosť je príchod dodávateľa, ktorý priniesol 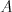 televízorov za
jednotkovú cenu
televízorov za
jednotkovú cenu 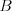 (môžete predpokladať, že
(môžete predpokladať, že 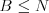 . Druhá udalosť je
príchod študenta, ktorý chce kúpiť
. Druhá udalosť je
príchod študenta, ktorý chce kúpiť 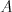 televízorov za čo najmenšiu cenu. Váš
program má vypísať túto cenu alebo "Nedostatok televízorov", ak Marek nemá dosť
televízorov na sklade. Ak Marek nemá dosť televízorov, študent od neho odchádza
s prázdnymi rukami.
televízorov za čo najmenšiu cenu. Váš
program má vypísať túto cenu alebo "Nedostatok televízorov", ak Marek nemá dosť
televízorov na sklade. Ak Marek nemá dosť televízorov, študent od neho odchádza
s prázdnymi rukami.
Príklad
Vstup
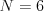
1 4 3
1 4 2
2 9
2 5
1 2 2
2 5
Výstup
Nedostatok televizorov
11
13
8. Ovplyvnenie predaja
25 bodov, kategória: O a T
Laci po nociach brigáduje, aby mal z čoho financovať svoj náročný študentský život (Keďže zadania čítajú aj neplnoleté osoby, nebudeme radšej zachádzať do detailov.). Najnovšie si našiel brigádu vo veľkoobchode Plesko, kde predáva televízory.
Predaj televízorov je ťažká práca, lebo televízory sú ťažké. A treba ich nosiť. A zákazníci stále chcú niečo extra. Napríklad minulý týždeň, keď tu boli tie dve slepice. Pekne sa ich spýtal, že či teda chcú farebný (napríklad zelený), a ony že to je jedno, hlavne nech dobre zrní...
Alebo včera, keď prišla nakupovať tá stará krysa. A že ona kašle na to či je zelený alebo cyklámenový, hlavne nech má veľa kanálov!
A na sklade sa hromadia zelené televízory, ktoré nik nechce.
A vtedy Laciho osvietilo a vymyslel skvelý zlepšovák. Spravia koleso šťastia. Vždy, keď niekto pôjde kúpiť televízor, zatočí si kolesom, aby zistil, aký dostane. Samozrejme, koleso bude len program na počítači, a ten vopred nastavia tak, aby pravdepodobnosti jednotlivých televízorov zodpovedali tomu, čo na začiatku mali v sklade. A už je Laci vo svojom živle -- namiesto fyzickej práce môže programovať.
Úloha
Na vstupe je počet druhov televízorov  a potom
a potom  reálnych čísel
reálnych čísel  .
Číslo
.
Číslo 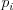 je pravdepodobnosť, s akou má na kolese vyjsť druh
je pravdepodobnosť, s akou má na kolese vyjsť druh  .
(Platí
.
(Platí 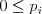 a tiež
a tiež 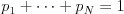 .)
.)
Máte k dispozícii funkciu random(), ktorá vždy, keď ju zavoláte, vráti náhodné
reálne číslo z intervalu 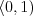 . Toto je jediný zdroj náhody, ktorý smiete
použiť (Ak váš programovací jazyk nemá presne takúto funkciu, v programe si túto
funkciu vyrobte pomocou toho, čo máte k dispozícii.).
. Toto je jediný zdroj náhody, ktorý smiete
použiť (Ak váš programovací jazyk nemá presne takúto funkciu, v programe si túto
funkciu vyrobte pomocou toho, čo máte k dispozícii.).
Napíšte program, ktorý načíta tieto údaje, spracuje ich a následne bude čo najrýchlejšie
generovať výstup -- čísla od 1 do  , pričom v každom kroku musí byť pravdepodobnosť toho,
že dostaneme výstup
, pričom v každom kroku musí byť pravdepodobnosť toho,
že dostaneme výstup  , rovná
, rovná 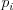 .
.
Obmedzenia a upozornenia:
Čas behu programu počas úvodného spracovania vstupu musí byť polynomiálny od  a nesmie závisieť od konkrétnych hodnôt
a nesmie závisieť od konkrétnych hodnôt 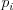 .
.
Za riešenie, ktoré na vygenerovanie jedného výstupu potrebuje čas priamo úmerný 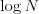 ,
veľa bodov nebude. A už tobôž nie za ešte pomalšie riešenia.
,
veľa bodov nebude. A už tobôž nie za ešte pomalšie riešenia.
Príklad
Vstup
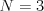
pravdepodobnosti: 0.7, 0.2, 0.1
Výstup
1, 1, 1, 3, 1, 1, 2, 1, 2, 3, 1, 1, 2, 1, ...
9. Tatranské panorámy
25 bodov, kategória: T
Keď mladý Anton na svojom farebnom televízore pozeral reláciu pre Národniarskych Geografov, ukazovali v nej ako vyrobiť z dvoch fotografií panorámu. Náruživý fotograf a programátor Anton sa rozhodol, že si na to vytvorí program.
Na vytvorenie panorámy zoberieme dve fotografie. Prvá bude naľavo a druhá napravo. Následne treba nájsť vertikálny prekryv týchto dvoch fotografií. Prekryv je nenulový počet stĺpcov pixelov na pravom kraji prvej fotografie, ktorý sa zhodne nachádza aj na ľavom kraji druhej fotografie. Keďže Anton chce čo najväčšie panorámy, potrebuje vždy nájsť prekryv, ktorý je minimálny. S týmto si však už nevie poradiť a preto bude potrebovať Vašu pomoc.
Úloha
Váš program bude pracovať s fotografiami v jemne-stratovom formáte ASCII. Vstup
programu začína dvomi číslami  ,
,  . Za nimi nasledujú dve matice znakov
. Za nimi nasledujú dve matice znakov 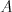 ,
,
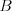 s rozmermi
s rozmermi 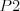 -- fotografie. Výstupom programu bude číslo
-- fotografie. Výstupom programu bude číslo  --
minimálny nenulový počet stĺpcov, ktorými sa dve fotografie prekrývajú. Formálne
sa dá prekryv vyjadriť nasledovne:
--
minimálny nenulový počet stĺpcov, ktorými sa dve fotografie prekrývajú. Formálne
sa dá prekryv vyjadriť nasledovne: 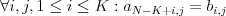 .
Ak takéto
.
Ak takéto  neexistuje, tak vypíšte
neexistuje, tak vypíšte 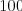 .
.
Príklad
Vstup
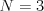 ,
, 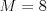
../\.... ./..\___ /....... ........ __../\.. ..\/..\_
Výstup
1
Komentár
(Výsledná panoráma vyzerá nasledovne:)../\........... ./..\____../\.. /........\/..\_ -----------------
10. Televízni lenivci
25 bodov, kategória: T
Georgova stavebná firma v poslednej dobe úspešne prosperuje. Preto sa snaží nájsť si svoje miesto aj v iných krajinách a presadzovať sa na tamojších trhoch. A tak sa nedávno stalo, že expandovala na veľký pracovný trh Lenivostanu.
Lenivostan je krajina, ktorej obyvatelia neoplývajú prílišnou usilovnosťou. Dá sa dokonca povedať, že sú nadmieru leniví a absolútne nemotivovaní. Preto aj prvá zákazka, ktorú dostala Georgova firma, dopadla ako dopadla -- po prvom dni nič nepripomínalo budúci aquapark. Viac to pripomínalo bandu lenivých robotníkov, váľajúcich sa na zemi a jediacich tresku. Preto sa Georg rozhodol, že si na kontrolu lenivých lenivcov zoženie účinné prostriedky -- kameru, pomocou ktorej bude schopný sledovať činnosť všetkých pracovníkov. Kameru umiestnil na vrtuľník, ktorý sa pohybuje nad staveniskom.
Keď sa robotníci dozvedeli, že ich práca bude takto neľudsky kontrolovaná,
spanikárili a rýchlo začali utekať niečo robiť. Celkovo sa každý robotník
dá popísať miestom, kde sa váľal a jedol tresku, a vektorom, ktorým sa rozbehol.
Robotníci majú v montérkach rôzne veľké a ťažké náradie, preto sa každý pohybuje
rôznou rýchlosťou. Avšak ich rýchlosť a ani smer ich behu sa nemení. Ak
má robotník  štartovnú pozíciu
štartovnú pozíciu ![[s_x, s_y]](http://old.ksp.sk/wiki/pub/cache/50443ec5cd4e344a5670fd79287092cc.png) a vektor jeho pohybu je
a vektor jeho pohybu je
![[v_x, v_y]](http://old.ksp.sk/wiki/pub/cache/4a7d4d6db1e9081d353c0a3a42646b77.png) , potom jeho pozícia v čase
, potom jeho pozícia v čase 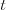 bude
bude ![[s_x+tv_x, s_y+tv_y]](http://old.ksp.sk/wiki/pub/cache/ad036636b05ab796379e12fc23832974.png) .
.
Georg, sediaci v kontrolnej veži staveniska, ich môže pozorovať na svojom televízore. Veľmi sa mu páči, ako pobehujú a úplne najviac sa mu páči, ak vidí, ako pobehujú všetci. Avšak na to potrebuje dosť veľký televízor, no a veľké televízory sú drahé televízory. Preto mu pomôžte a zistite, aký najmenší televízor mu stačí, aby aspoň na chvíľočku videl na obrazovke všetkých robotníkov, ak bude kamera snímať správnu oblasť staveniska!
Keďže v Lenivostane boli takí leniví, že ešte nevymysleli obdĺžnik, tak obrazovky všetkých televízorov majú tvar štvorca. Pre jednoduchosť v tomto zadaní predpokladáme, že oblasť, ktorú možno pozorovať na obrazovke televízora, je priamo úmerná veľkosti obrazovky. Rovnako predpokladáme, že oblasť, ktorú sníma kamera, má tvar štvorca a ten má navyše svoje strany rovnobežné so súradnicovými osami.
Úloha
Pre dané pozície a vektory robotníkov zistite, aký najmenší televízor si musí Georg kúpiť, aby aspoň v jednom momente videl všetkých robotníkov. Keďže obrazovka televízora má tvar štvorca, výstupom by malo byť jedno reálne číslo -- veľkosť jej hrany. Robotník, ktorý je presne na hranici záberu, sa považuje za zachyteného. V príkladoch je pri robotníkoch uvedený najprv štartový bod a potom vektor posunu.
Príklad
Vstup
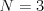
Robotník 1: ![[-4,0],(3,0)](http://old.ksp.sk/wiki/pub/cache/7e9e31ab5277d35215bdf72d98b408ca.png)
Robotník 2: ![[1,3],(0,-1)](http://old.ksp.sk/wiki/pub/cache/094b8e10b63c63793ab83f592b51fc43.png)
Robotník 3: ![[4,1],(-1,0)](http://old.ksp.sk/wiki/pub/cache/310b4ad22e0c113f3effa8f369cb8f03.png)
Výstup
1
(O dve sekundy bude pozícia prvého robotníka ![[2,0]](http://old.ksp.sk/wiki/pub/cache/6d332e510140eb04f2d19e3e2d763f1e.png) , druhého
, druhého ![[1,1]](http://old.ksp.sk/wiki/pub/cache/e9dee7b604221fe4dd67ddfd16fc96e5.png) a tretieho
a tretieho ![[2,1]](http://old.ksp.sk/wiki/pub/cache/1a41fc0cf98c398a71c0e08f824a42e3.png) .)
.)
Vstup
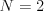 Robotník 1:
Robotník 1: ![[0,0],(1,1)](http://old.ksp.sk/wiki/pub/cache/c154201d47e60361e2d11358a92a6460.png) Robotník 2:
Robotník 2: ![[3,4],(1,1)](http://old.ksp.sk/wiki/pub/cache/5b7c18b265c2b0aa495ffb7e00428280.png)
Výstup
4