Milé naše riešiteľky, milí naši riešitelia,
Užite si prvú sériu letnej časti.
Termín odoslania riešení tejto série je pondelok 8. marca 2010.
Kto sa veľmi namáha, skoro ustane.
1. Zablatená cesta
10 bodov, kategória Z
Aj keď sa to možno nezdá, Petržlen je cyklistického neba hviezda. Dobre, troška to preháňame. Ale
Petržlen si veľmi rád zabicykluje. Dnes sa rozhodol,
že by sa rád na bicykli vydal do Blatislavy.
Aby si nezničil nohy, chce sa počas celej cesty stále namáhať rovnako.
No okolo Blatislavy je veľa blata a navyše nerovnomerne rozdeleného.
A čím ho je viac, tým ťažšie sa po ňom ide.
Aby sa cestou Petržlen nenudil, zoberie si MP3 prehrávač, v ktorom má svoj obľúbený playlist. Teraz sa ale trápi: ako veľmi má makať, aby mu cesta do Blatislavy trvala presne toľko isto ako je dĺžka jeho playlistu? Navyše v najnovších časopisoch sa dočítal, že má makať rovnomerne, lebo vtedy sa najmenej unaví.
Úloha
Petržlenov playlist má dĺžku 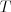 hodín.
Cesta do Blatislavy je tvorená
hodín.
Cesta do Blatislavy je tvorená  rovnako dlhými úsekmi. Každý z úsekov má dĺžku
rovnako dlhými úsekmi. Každý z úsekov má dĺžku 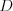 .
Na úseku číslo
.
Na úseku číslo  je množstvo blata rovné
je množstvo blata rovné 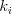 .
Ak bude Petržlen šľapať tak, že po úseku bez blata pôjde rýchlosťou
.
Ak bude Petržlen šľapať tak, že po úseku bez blata pôjde rýchlosťou  , tak po úseku
kde je
, tak po úseku
kde je 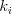 blata pôjde rýchlosťou
blata pôjde rýchlosťou 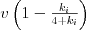 .
.
Napíšte program, ktorý načíta čísla 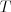 ,
,  ,
, 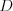 a
a 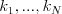 a vypočíta takú rýchlosť
a vypočíta takú rýchlosť  , pre ktorú bude Petržlenovi celá cesta trvať presne
, pre ktorú bude Petržlenovi celá cesta trvať presne 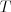 hodín.
Odpoveď stačí vypísať vhodne zaokrúhlenú.
hodín.
Odpoveď stačí vypísať vhodne zaokrúhlenú.
Príklad
Vstup
3 2 5
0 4
Výstup
5.000000
''Prvým úsekom pôjde rýchlosťou 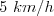 , druhým rýchlosťou
, druhým rýchlosťou 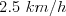 . Prvý úsek prejde
za hodinu a druhý za dve.''
. Prvý úsek prejde
za hodinu a druhý za dve.''
Vstup
7 4 12
4 8 0 11
Výstup
16.714286
Pre  budú Petržlenovi jednotlivé úseky trvať približne
budú Petržlenovi jednotlivé úseky trvať približne 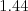 ,
, 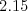 ,
, 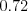 a
a 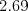 hodiny.
hodiny.
2. Zmrzlináreň
10 bodov, kategória Z
Nedávno sa na matfyze objavila zmrzlináreň. Má veľký úspech, lebo tam predávajú zmrzlinu s rôznymi
exotickými príchuťami a dokonca aj s rôznymi tvarmi kopčeka. Okrem tradičných guľových kopčekov sú v ponuke
kockové, valcové, ihlanové, ba dokonca aj trojstenové!
Najdrsnejšia príchuť v ponuke je karamelovo-muchotrávková, druhá je slivkovo-rybacia a tretia najdrsnejšia je punčovo-paštétová. Tieto tri príchute dokážu občas poriadne zatočiť žalúdkom. Ostatné príchute nie sú vôbec drsné a žalúdkom netočia.
Presnejšie, funguje to nasledovne. Vždy, keď príde do žalúdka kopček zmrzliny, pozrie sa na všetky kopčeky, ktoré tam už sedia. A vždy, keď uvidí kopček, ktorý má menej drsnú príchuť ako on sám, tak raz zatočí žalúdkom.
Úloha
Maják práve nalačno zjedol  zmrzlín. Na vstupe je číslo
zmrzlín. Na vstupe je číslo  a postupnosť príchutí zmrzlín v
poradí, v akom ich Maják zjedol. Napíšte program, ktorý spočíta, koľkokrát sa Majákovi počas
jedenia zatočil žalúdok.
a postupnosť príchutí zmrzlín v
poradí, v akom ich Maják zjedol. Napíšte program, ktorý spočíta, koľkokrát sa Majákovi počas
jedenia zatočil žalúdok.
Príklad
Vstup
7
karamelovo-muchotravkova
slivkovo-rybacia
puncovo-pastetova
slivkovo-rybacia
jahodova
malinova
karamelovo-muchotravkova
Výstup
6
Prvé tri kopčeky Majákovi žalúdok nezatočili, lebo každá príchuť je menej drsná ako tie pred ňou. Štvrtý kopček mu zatočil žalúdok 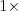 . Piaty a šiesty kopček sú obyčajné príchute, ktoré žalúdkom netočia. No a posledný, siedmy kopček zatočí žalúdkom hneď
. Piaty a šiesty kopček sú obyčajné príchute, ktoré žalúdkom netočia. No a posledný, siedmy kopček zatočí žalúdkom hneď 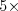 .
.
3. Zvukové bariéry
10 bodov, kategória Z
V Absurdistane, krásnej to krajine, vedie diaľničný obchvat hlavného mesta
absurdne krížom cez mesto a význam slova "obchvat" tým dostal jedinečne
národný charakter. Obyvateľom z tesnej blízkosti obchvatu sa však vôbec
nepáčil hluk áut, ktorý je slýchať vo dne i v noci.
Pod tlakom obyvateľstva sa tak Národná Diaľničná Spoločnosť Absurdistanu rozhodla postaviť okolo obchvatu zvukové bariéry. Aby sa podporila domáca výroba, nakúpili izolačné bloky od domácej firmy a tak sú tieto bloky rozličných i dosť divokých tvarov. Z toho inžinieri veru radosť nemali; veď uznajte, ako z takých exotických blokov postaviť pekný múr? Inžinierom sa to riešiť veru nechcelo, nuž rozhodli sa nechať to na žeriavnikov, veď oni to už dáko poskladajú. Chyba. Žeriavnici, nemajúc nad sebou kontrolu, ukladali dielce tak, ako im pod ruku, či vlastne pod hák (Hádanka: Ruka, klepeto i hák a pritom to nie je pirát! Kto je to?) prišli.
Stimulovaní týmito udalosťami sa inžinieri rozhodli žeriavnikov kontrolovať, aby múry konečne boli múrmi. Robiť to osobne sa im však samozrejme nechce, ale už to nemôžu nechať na náhodu a tak sa rozhodli zveriť túto úlohu niekomu z radov zahraničných odborníkov. Spomedzi všetkých si vybrali práve teba! Veríme, že nám v Absurdistane neurobíš hanbu.
Úloha
Teraz trocha formálnejšie. Na prvom riadku vstupu sú 4 prirodzené čísla: dĺžka múru 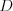 , výška múru
, výška múru 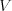 ,
počet typov blokov
,
počet typov blokov 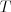 a počet blokov
a počet blokov  , ktoré žeriavnik na stavbu múru použil.
, ktoré žeriavnik na stavbu múru použil.
Nasleduje popis 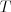 typov blokov v poradí
typov blokov v poradí  : šírka
: šírka 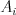 a výška
a výška
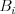
 -teho typu a
-teho typu a 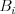 riadkov, každý po
riadkov, každý po 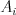 znakoch "
znakoch "X" alebo
"-" popisujúcich tvar bloku. Môžete predpokladať, že každý blok je
súvislý (Ak je blok väčší ako 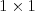 , každé "
, každé "X" sa dotýka
aspoň jedného iného "X" hranou, nie len rohom.), neprázdny a nie je väčší
ako samotný múr.
Nasleduje  riadkov: postupnosť, ako žeriavnik ukladal bloky. Riadok,
ktorý je
riadkov: postupnosť, ako žeriavnik ukladal bloky. Riadok,
ktorý je 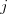 -ty v~poradí obsahuje dve prirodzené čísla, a to polohu
-ty v~poradí obsahuje dve prirodzené čísla, a to polohu 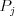 , kam
bol umiestnený blok typu
, kam
bol umiestnený blok typu 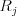 (
(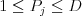 a
a 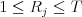 ). Ak hovoríme,
že blok bol položený na polohu
). Ak hovoríme,
že blok bol položený na polohu 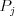 , myslíme tým, že na túto pozíciu bol
zarovnaný ľavý bok tohto bloku a ten bol takto položený. Môžete tiež
predpokladať, že žiaden blok neprekročí dĺžku múru, výšku ale môže.
, myslíme tým, že na túto pozíciu bol
zarovnaný ľavý bok tohto bloku a ten bol takto položený. Môžete tiež
predpokladať, že žiaden blok neprekročí dĺžku múru, výšku ale môže.
Vašou úlohou je odpovedať "ANO" alebo "NIE" na otázku, či sa zadanou postupnosťou
postavil súvislý múr -- obdĺžnik, ktorý nemá diery a má rozmery presne 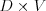 .
.
Príklad
Vstup
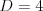
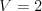
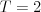
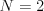
4 1
XXXX
1 1
X
1 2
1 1
Výstup
NIE
chceme
XXXX
XXXX
dostaneme ale
XXXX
X---
Vstup
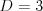
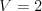
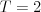
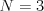
3 2
X--
XXX
1 1
X
1 1
2 2
3 2
Výstup
ANO
4. Zaplať a leť
15 bodov, kategórie Z a O
Arina je veľmi sporivá žienka, avšak keď zbadala reklamu na novú leteckú
spoločnosť LAMA (Lost Airports Magic Airlines), nemohla odolať.
Ponúkajú totiž lety na stratené letiská pomocou magických lietadiel. V~jednom
okamihu ste na jednom letisku a v tom druhom už ste na inom letisku, ani sa
nenazdáte.
No odolali by ste? Arina totiž vždy chcela vidieť letisko spoločnosti IBM (Institute of Black Magic). A ono je dokonca v ponuke! Avšak ako každá novinka, ani tieto lety nie sú práve najlacnejšie a dokonca nie vždy existuje priamy let. Preto by potrebovala vedieť, koľko ju to bude najmenej stáť, aby mohla začať šetriť.
Preto si opísala všetky lety, čo existujú, a zistila, že letisko IBM je tzv.
koncové letisko, čiže je to letisko, z ktorého sa už letieť inam touto
spoločnosťou nedá. Dokonca je jediné také. Ó, tá pocta! Ale čože je toto,
všetky letiská majú dokonca svoje číslo a lety vedú len na niektoré z ďalších
letísk, nikdy nie späť. To len potvrdzuje staré príslovie "Všetky cesty vedú do
IBM"! Arina sa pousmiala, ale potom zazúfala; kto jej pomôže a povie, koľko si
má našetriť? Preto sa obrátila na vás, milí KSPáci
Úloha
Na vstupe dostanete  (počet letísk) a
(počet letísk) a  (počet liniek, ktoré medzi nimi
premávajú). Na ďalších
(počet liniek, ktoré medzi nimi
premávajú). Na ďalších  riadkoch budú popisy letov v tvare "
riadkoch budú popisy letov v tvare "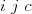 " (bez
úvodzoviek), ktoré sú utriedené vzostupne podľa
" (bez
úvodzoviek), ktoré sú utriedené vzostupne podľa  (a následne aj podľa
(a následne aj podľa 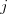 );
);
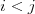 a let vedie z letiska
a let vedie z letiska  na letisko
na letisko 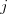 a stojí
a stojí  .
.
Na výstup vypíšte, koľko stojí najlacnejšia cesta z letiska 1 na letisko  .
Ak taká neexistuje, vypíšte string "
.
Ak taká neexistuje, vypíšte string "neexistuje".
Môžete predpokladať, že 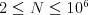 ,
,  ,
, 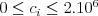 a že medzi každou dvojicou staníc existuje maximálne jeden let.
a že medzi každou dvojicou staníc existuje maximálne jeden let.
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdávať jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a~dostane body podľa toho, na koľkých vstupoch dá správny výsledok v~časovom limite.
Príklad
Vstup
4 6
1 2 4
1 3 3
1 4 15
2 3 1
2 4 10
3 4 2
Výstup
5
5. Opravovacia lotéria vracia úder
15 bodov, kategórie Z a O
V prvej sérii sme boli svedkami toho, ako sa lotéria opravovateľského Impéria
zrútila ako domček z karát. Impérium sa ale rozhodlo, že to len tak nenechá a
pripravilo novú, lepšiu lotériu. Ste pripravení zasadiť jej úder priamo do
jadra?
V tejto úlohe sa opäť rozdávajú body zadarmo. Stačí, keď nám pošlete reťazec 32 znakov malej anglickej abecedy (napr. "abcdefghijklmnopqrstuvwxyzabcdef") a môžete aj vy nejaké body vyhrať!
Počet bodov, ktoré dostanete, bude rovný tomu, čo pre vaše číslo vypíše nasledujúci program:
- #include <cstdio>
- #include <cmath>
- int sbox1[] = {4, 10, 11, 15, 24, 16, 17, 1, 6, 9, 3, 22, 19, 2, 0, 23, 25, 18, 13, 8, 5, 21, 7, 12, 14, 20};
- int sbox2[] = {2, 0, 20, 13, 11, 17, 4, 3, 9, 18, 23, 15, 24, 6, 16, 14, 22, 10, 25, 12, 21, 8, 7, 5, 19, 1};
- #define NUM_ROUNDS 2234567890123ll
- char key[] = "bazavektorovehopriestoru";
- long long countpoints(char *a)
- {
- long long ret = 0;
- for(int i = 0; i < 32; i++)
- for(int j = i + 1; j < 32; j++)
- if(sbox1[a[i]-'a'] == sbox2[a[j]-'a'])
- ret++;
- return ret;
- }
- void round(char *in, char *out)
- {
- for(int i = 0; i < 16; i++)
- out[i+16] = 'a' + sbox2[in[i]-'a'];
- for(int i = 16; i < 32; i++)
- out[i-16] = 'a' + sbox1[(in[i-16]-'a' + in[i]-'a' + key[i-16]-'a') % 26];
- out[32] = 0;
- }
- int main()
- {
- char text[2][35];
- int ind = 0;
- scanf("%s", text[ind]);
- for(long long i = 0; i < NUM_ROUNDS; i++){
- round(text[ind], text[1 - ind]);
- ind = 1 - ind;
- }
- printf("%s\n", text[ind]);
- printf("%d\n", (int)sqrt(countpoints(text[ind]) / 2.0 + 8) - 1);
- }
Program je písaný v C++. Ak budete dobre hľadať, na webstránke KSP nájdete aj ekvivalentné programy napísané v Pascale a možno aj v iných jazykoch (Brainfuck ale nečakajte).
V tejto úlohe nám neposielajte žiadne programy. Jediné, čo budeme hodnotiť, je konkrétny reťazec, ktorý odovzdáte. (Neurazíme sa, ak nám k nemu napíšete pár viet o tom, ako ste sa k tomu konkrétnemu reťazcu dostali.)
Pascalovsky program:
- var sbox1:array[0..25] of integer = (4, 10, 11, 15, 24, 16, 17, 1, 6, 9, 3, 22, 19, 2, 0, 23, 25, 18, 13, 8, 5, 21, 7, 12, 14, 20);
- sbox2:array[0..25] of integer = (2, 0, 20, 13, 11, 17, 4, 3, 9, 18, 23, 15, 24, 6, 16, 14, 22, 10, 25, 12, 21, 8, 7, 5, 19, 1);
- numRounds:int64;
- key:array[0..23] of char = ('b','a','z','a','v','e','k','t','o','r','o','v','e','h','o','p','r','i','e','s','t','o','r','u');
- round:int64;
- c:integer;
- ind:integer;
- data:array[0..1] of array [0..31] of char;
- function countPoints(a:array of char):integer;
- var i,j:integer;
- begin
- countPoints:=0;
- for i:=0 to 31 do begin
- for j:=i+1 to 31 do begin
- if(sbox1[ord(a[i])-ord('a')] = sbox2[ord(a[j])-ord('a')]) then
- countPoints:=countPoints+1;
- end;
- end;
- end;
- procedure kolo(input:array of char; var out:array of char);
- var i:integer;
- begin
- for i:=0 to 15 do
- out[i+16]:= char(ord('a') + sbox2[ord(input[i])-ord('a')]);
- for i:=16 to 31 do
- out[i-16]:= char(ord('a') + sbox1[(ord(input[i-16])-ord('a') + ord(input[i])-ord('a') + ord(key[i-16])-ord('a')) mod 26]);
- end;
- begin
- numRounds:=2234567*1000000+890123;
- round:=0;
- for c:=0 to 31 do
- read(data[0][c]);
- ind:=0;
- while round < numRounds do begin
- kolo(data[ind], data[1 - ind]);
- ind:= 1 - ind;
- round:=round+1;
- end;
- writeln(int(sqrt(countpoints(data[ind]) / 2.0 + 8) - 1));
- end.
6. O kráľových jedoch
20 bodov, kategória O
Kráľ Baltazár (prezývaný tiež Baltýk) usporiadal obrovskú kráľovskú
hostinu, na ktorú pozval všetkých svojich priateľov aj
nepriateľov, skrátka každého. A ako správny hostiteľ, chcel na nej
otráviť všetkých svojich nepriateľov. Plán bol veľmi jednoduchý. Každý
hosť donesie na hostinu fľašu vína. Priatelia určite donesú kvalitné víno,
nepriatelia zase určite donesú kvalitne otrávené víno. Stačí teda každému
dať sa napiť vína, ktoré priniesol.
Hostina začala, ale čo sa nestalo. Kvalitné vína sa pomiešali s kvalitne otrávenými tak, že nik nevedel povedať, ktoré je ktoré. Našťastie má kráľ niekoľko sluhov, ktorým môže dať ochutnať víno, prípadne zmes vín. Sluha po ochutnaní zomrie práve vtedy, ak aspoň jedno z vín v zmesi, ktorú pil, bolo otrávené. Kráľovi je testovanie vína na sluhoch nepríjemné, preto by chcel otrávené vína nájsť na čo najmenej pokusov.\footnote{počet pokusov nie je to isté ako počet mŕtvych sluhov}
Úloha
Máme  vín, z čoho práve
vín, z čoho práve  je otrávených. Vašou úlohou je napísať program,
ktorý bude radiť kráľovi, ako má testovať vína tak, aby identifikoval všetky
otrávené vína. Vína sú pre jednoduchosť očíslované od
je otrávených. Vašou úlohou je napísať program,
ktorý bude radiť kráľovi, ako má testovať vína tak, aby identifikoval všetky
otrávené vína. Vína sú pre jednoduchosť očíslované od 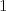 po
po  . Program bude
musieť fungovať nasledovne:
. Program bude
musieť fungovať nasledovne:
- Načíta
 a
a  .
.
- Vypíše počet
 a čísla
a čísla  vín, ktoré sa majú zmiešať a dať vypiť sluhovi.
vín, ktoré sa majú zmiešať a dať vypiť sluhovi.
- Načíta, či sluha po vypití zmesi vín zomrel.
- Ak vie, ktoré vína sú otrávené, tak vypíše ich čísla a skončí, inak pokračuje krokom
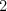 .
.
Bodovanie:
Prvoradým kritériom hodnotenia bude počet pokusov, druhoradým
časová a pamäťová zložitosť. Pri hodnotení počtu otázok ignorujeme
konštanty, podobne ako pri časovej a pamäťovej zložitosti.
Riešenie potrebujúce 47-krát viac otázok ako optimálne teda môže
získať plný počet bodov, ale riešenie s $K$-krát viac otázkami
už nie. (Formálne: Nech 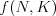 je počet pokusov, ktoré potrebuje
algoritmus
je počet pokusov, ktoré potrebuje
algoritmus 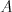 pri
pri  vínach, z ktorých je
vínach, z ktorých je  otrávených. Potom každý
algoritmus, ktorý potrebuje
otrávených. Potom každý
algoritmus, ktorý potrebuje 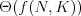 pokusov, budeme považovať
za rovnako dobrý, čo sa počtu otázok týka.) Navyše predpokladáme, že
pokusov, budeme považovať
za rovnako dobrý, čo sa počtu otázok týka.) Navyše predpokladáme, že  je ďaleko menšie ako
je ďaleko menšie ako  .
.
Súčasťou riešenia by mal byť aj odhad počtu pokusov v závislosti od  a
a  , aj s~dôkazom,
že je odhad správny. Samozrejme, program musí byť správny a teda vždy označiť ako otrávené
práve tie vína, ktoré sú otrávené.
, aj s~dôkazom,
že je odhad správny. Samozrejme, program musí byť správny a teda vždy označiť ako otrávené
práve tie vína, ktoré sú otrávené.
Príklad
vstup: 10 2
program: 3 1 2 3
vstup: sluha zomrel
program: 3 1 4 5
vstup: sluha zomrel
program: 4 1 3 4 7
vstup: sluha nezomrel
program: otravene su 2 a 5
7. O godzillích dostihoch
20 bodov, kategória O
Mišo s Majákom si zasa vymysleli novú hru. Jej pravidlá sú veľmi jednoduché:
Hra je určená pre 2 hráčov. Hrací plán sa skladá z radu  políčok, ktoré sú očíslované zaradom
od 0 po
políčok, ktoré sú očíslované zaradom
od 0 po  . Na políčko číslo
. Na políčko číslo  sa položí figúrka Godzilly. Táto figúrka má na začiatku hry
rýchlosť 0. Hráči teraz striedavo ťahajú. Ťah hráča spočíva v tom, že sa rozhodne, či
chce rýchlosť figúrky o 1 zvýšiť, o 1 znížiť, alebo nechať nezmenenú. (Pritom ale počas
hry musí byť rýchlosť stále kladná.)
Godzillu hráč následne pohne smerom k políčku 0 toľkokrát, aká je jej aktuálna rýchlosť.
sa položí figúrka Godzilly. Táto figúrka má na začiatku hry
rýchlosť 0. Hráči teraz striedavo ťahajú. Ťah hráča spočíva v tom, že sa rozhodne, či
chce rýchlosť figúrky o 1 zvýšiť, o 1 znížiť, alebo nechať nezmenenú. (Pritom ale počas
hry musí byť rýchlosť stále kladná.)
Godzillu hráč následne pohne smerom k políčku 0 toľkokrát, aká je jej aktuálna rýchlosť.
Hru vyhrá ten, kto vo svojom ťahu dosiahne políčko 0 (prípadne prejde cez neho), a to aj vtedy, keby ešte mal v danom ťahu pohyb Godzilly pokračovať.
Príklad:
Godzilla stojí na políčku 11 a jej aktuálna rýchlosť je 7. Na ťahu je Mišo. Rozhodne sa znížiť
rýchlosť na 6 a následne posunie Godzillu na políčko číslo 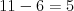 . V nasledujúcom
ťahu Maják vyhrá, bez ohľadu na to, ako sa rozhodne zmeniť rýchlosť.
. V nasledujúcom
ťahu Maják vyhrá, bez ohľadu na to, ako sa rozhodne zmeniť rýchlosť.
Hra vzbudila značný dojem a ostatní KSPáci začali tipovať, kto kedy vyhrá. Mio sa rozhodol na tejto hre zbohatnúť, no tipovanie mu veľmi nejde, preto vás žiada o radu.
Úloha
Vašou úlohou je napísať program, ktorý pre dané  vypíše, ktorý hráč vyhrá, ak budú hrať obaja
optimálne. Hru vždy začína Mišo.
vypíše, ktorý hráč vyhrá, ak budú hrať obaja
optimálne. Hru vždy začína Mišo.
Príklad
Vstup
8
Výstup
Majak vyhra.
8. Tragédia
25 bodov, kategórie O a T
Ach, kam sa to zase dostal? Georg (čítaj [georg]), svetoznámy scenárista
a režisér, sa po riadnom kopnutí múzou ocitol uprostred ničoho, v obci Nalomená
Trieska. Myslel si, že odrezaný od civilizácie sa bude môcť plne sústrediť na
svoju najnovšiu autobiografickú jednoaktovku s pracovným názvom "Utrpenie
mladého Georga". To sa mu síce podarilo a~dokonca už má náčrt scenára, ale
zabudol na jeden nepríjemný detail. V Nalomenej Trieske nie je divadlo. Starosta
našťastie podporuje umenie a~preto poskytol Georgovi na skúšanie šatňu miestnej
materskej školy. Tiež sa prihlásilo zopár obyvateľov so záujmom o~dosky
znamenajúce svet, ktorých budeme pre jednoduchosť nazývať v ďalšom texte
hercami (aj keď tak vôbec nevyzerajú).
Začalo sa skúšať. Jednoaktovka sa skladá z jedného dejstva, ktoré sa delí na scény a tie sa delia na vety. Na začiatku každej scény prídu z jedálne (improvizované zákulisie) do šatne (improvizované javisko) herci, ktorí majú počas tejto scény vystupovať. Odohrajú si svoje úlohy, vyrieknu svoje repliky a na konci scény sa znova vrátia do jedálne. No prišla zima a v šatni je zrazu pomenej miesta. Herci naďalej skúšajú, hlava-nehlava, noha-nenoha. Ako sa tak v zápale dialógov prechádzajú po šatni a prekračujú porozhadzované topánky, občas niektorý herec stúpi inému na nohu. Presnejšie, počas jednej scény stúpi každý herec každému hercovi na nohu práve raz. Aj sebe (naozaj je tam málo miesta). Herci s pošliapanými nohami hrajú o poznanie horšie, preto chce Georg zakročiť. Plánuje rozdeliť svoju jednoaktovku na scény tak, aby bolo dokopy šliapnutí na nohu čo najmenej.
Úloha
Stručne a (snáď) jasne: rozdeľte postupnosť čísel na súvislé úseky tak, aby po sčítaní druhých mocnín počtu rozdielnych čísel v každom úseku vyšiel čo najmenší výsledok.
Podrobnejšie: na vstupe dostanete v prvom riadku dve čísla  (počet viet v~Georgovom
scenári,
(počet viet v~Georgovom
scenári, 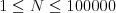 ) a
) a  (počet hercov,
(počet hercov, 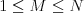 )
oddelené medzerou. V druhom riadku nasledujú čísla
)
oddelené medzerou. V druhom riadku nasledujú čísla 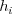 pre
pre 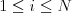 oddelené medzerami; vetu
oddelené medzerami; vetu  má vyriecť herec číslo
má vyriecť herec číslo 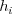 (
(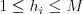 ).
Vašou úlohou je nájsť také rozdelenie viet na scény, ktoré minimalizuje
celkový počet šliapnutí na nohu a~vypísať tento počet. Každá scéna musí pokrývať
súvislý úsek viet a každá veta sa musí nachádzať práve v~jednej scéne. Počas
scény, v ktorej vystupuje
).
Vašou úlohou je nájsť také rozdelenie viet na scény, ktoré minimalizuje
celkový počet šliapnutí na nohu a~vypísať tento počet. Každá scéna musí pokrývať
súvislý úsek viet a každá veta sa musí nachádzať práve v~jednej scéne. Počas
scény, v ktorej vystupuje 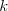 hercov, nastane
hercov, nastane 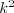 šliapnutí na nohu.
A~samozrejme, kto nemá v scéne vetu, nevystupuje v nej (teta kuchárka občas
nechá v jedálni chladnúť pečené buchty a vtedy je problém dostať na javisko aj
tých, ktorí majú v scéne vystupovať).
šliapnutí na nohu.
A~samozrejme, kto nemá v scéne vetu, nevystupuje v nej (teta kuchárka občas
nechá v jedálni chladnúť pečené buchty a vtedy je problém dostať na javisko aj
tých, ktorí majú v scéne vystupovať).
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdávať jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v~časovom limite.
Príklad
Vstup
7 4
3 1 4 1 1 4 1
Výstup
5
Optimálne je rozdelenie na dve scény. V~prvej bude len prvá veta, ktorú má vyriecť herec číslo 3 (1 šliapnutie), v~druhej scéne budú zvyšné vety, ktoré majú vyriecť herci 1 a~4 (4 šliapnutia).
9. Tajný plán škorca Jonáša
25 bodov, kategória T
Na starej čerešni sa premnožili húsenice. Ale pst, nepovedzte to nikomu!
Jonáš je zatiaľ jediný škorec, ktorý o tom vie. A plánuje tam hneď zajtra
zaletieť a napráskať sa, čo to dá.
Samozrejme si to ale najskôr potrebuje dobre naplánovať. A tu by sa mu zišla
vaša pomoc.
Čerešňa je strom. Keď sa na ňu pozeráme ako na graf, má 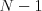 hrán
(konárov a kusov kmeňa medzi vetveniami) a
hrán
(konárov a kusov kmeňa medzi vetveniami) a  vrcholov s číslami
od
vrcholov s číslami
od 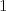 po
po  (miesta vetvenia, konce konárov a miesto, kde sa dotýka zeme).
O každej hrane vie Jonáš počet húseníc, ktoré na nej žijú.
(miesta vetvenia, konce konárov a miesto, kde sa dotýka zeme).
O každej hrane vie Jonáš počet húseníc, ktoré na nej žijú.
Jonášov plán vyzerá nasledovne: pristane na strome vo vrchole 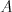 a
následne prelezie po hranách do vrcholu
a
následne prelezie po hranách do vrcholu 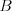 a cestou vyžerie
všetky húsenice. Samozrejme, pôjde tak, aby nešiel po žiadnej hrane viackrát
(ísť po konári, kde už nie sú húsenice, je strata času).
a cestou vyžerie
všetky húsenice. Samozrejme, pôjde tak, aby nešiel po žiadnej hrane viackrát
(ísť po konári, kde už nie sú húsenice, je strata času).
Úloha
Napíšte program, ktorý načíta popis stromu, spracuje si ho a následne bude
Jonášovi odpovedať na otázky. Každá otázka má tvar: "koľko húseníc zožeriem,
ak prejdem z vrcholu 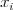 do vrcholu
do vrcholu 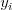 ?"
?"
Hodnotenie:
aby ste dostali nejaké zaujímavé body, je nutné splniť nasledujúce
dve podmienky: 1. Čas potrebný na spracovanie stromu musí byť lepší ako
kvadratický od  . 2. Najhorší čas potrebný na zodpovedanie otázky musí byť lepší ako
lineárny od
. 2. Najhorší čas potrebný na zodpovedanie otázky musí byť lepší ako
lineárny od  .
.
Pri dodržaní týchto dvoch podmienok bude primárnym kritériom hodnotenia časová zložitosť odpovedania na otázky, sekundárnym časová zložitosť predspracovania a terciárnym pamäťová zložitosť.
Príklad
Vstup
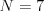
hrany: 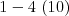 ,
, 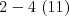 ,
, 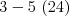 ,
, 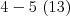 ,
, 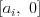 ,
, 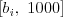 .
.
otázky:
1 3
2 3
Výstup
47
48
V popise vstupu "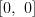 " predstavuje hranu medzi vrcholmi
" predstavuje hranu medzi vrcholmi  a
a 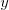 so
so  húsenicami. Formát vstupu si samozrejme zvoľte vlastný.
húsenicami. Formát vstupu si samozrejme zvoľte vlastný.
''Prvý výstup: Na ceste z 1 do 3 pôjde cez vrcholy 4 a 5 a zožerie 10+13+24=47 húseníc.''
10. Túžba po majetku
25 bodov, kategória T
Starý a bohatý gróf deMaroschko umrel a zanechal na tomto svete  synov a veľký majetok
vo forme obrovského pozemku a nehnuteľností. Nehnuteľností je
synov a veľký majetok
vo forme obrovského pozemku a nehnuteľností. Nehnuteľností je  a sú porozmiestňované
po celom pozemku. Pôda ako taká je v tejto lokalite bezcenná, avšak každá z nehnuteľností
predstavuje veľmi atraktívny a hodnotný objekt. Je medzi nimi napríklad ZOO s Godzillami alebo
továreň na konzervy s ananásom.
a sú porozmiestňované
po celom pozemku. Pôda ako taká je v tejto lokalite bezcenná, avšak každá z nehnuteľností
predstavuje veľmi atraktívny a hodnotný objekt. Je medzi nimi napríklad ZOO s Godzillami alebo
továreň na konzervy s ananásom.
Problém spočíva v tom, že poslednú vôľu nešťastnou náhodou zjedla lama pred tým,
ako si ju stačili právnici prečítať. No a ako to už býva,  nenásytných synov
chce túto situáciu využiť a uchmatnúť si pre seba čo najviac z majetku starého grófa.
nenásytných synov
chce túto situáciu využiť a uchmatnúť si pre seba čo najviac z majetku starého grófa.
Každý zo synov zaslal písomný nárok, v ktorom sa dožaduje obdĺžnikovej časti pozemku so všetkými nehnuteľnosťami, ktoré sa nachádzajú vnútri alebo na okraji daného územia. Všetci tvrdia, že gróf im to ústne sľúbil a že sa to určite nachádzalo v poslednej vôli. Hlavný problém je, že sa dané nároky prekrývajú. Územia by sa ešte pahltní potomkovia dokázali vzdať, avšak nehnuteľností sa nevzdajú nikdy.
Zamestnanci pozemkového úradu teraz spolu s právnikmi grófových ratolestí sedia nad písomnými nárokmi a snažia sa nájsť riešenie, s ktorým budú všetky zúčastnené strany súhlasiť. Aby mali ľahšiu prácu, potrebovali by o každej nehnuteľnosti vedieť, súčasťou koľkých nárokov je. Detí a nehnuteľností je ale príliš veľa, a preto by potrebovali program. A ten program musí byť rýchly. Pretože keď nebude rýchly, štát utratí veľa za súdne prieťahy.
Úloha
Na vstupe sú čísla  a
a  -- počet nárokov a počet nehnuteľností. Nasleduje
-- počet nárokov a počet nehnuteľností. Nasleduje  riadkov popisujúcich nároky.
Každý nárok je popísaný ľavým horným bodom a pravým dolným bodom. Potom nasleduje
riadkov popisujúcich nároky.
Každý nárok je popísaný ľavým horným bodom a pravým dolným bodom. Potom nasleduje  riadkov s
pozíciami nehnuteľností (nehnuteľnosti si predstavíme ako body v rovine). Pre každú
nehnuteľnosť vypíšte, do koľkých nárokov spadá. Všetky súradnice sú celé čísla, ktoré v absolútnej hodnote neprevyšujú
1,000,000,000. Pri vymýšľaní algoritmu pamätajte na to, že
riadkov s
pozíciami nehnuteľností (nehnuteľnosti si predstavíme ako body v rovine). Pre každú
nehnuteľnosť vypíšte, do koľkých nárokov spadá. Všetky súradnice sú celé čísla, ktoré v absolútnej hodnote neprevyšujú
1,000,000,000. Pri vymýšľaní algoritmu pamätajte na to, že  aj
aj  môže byť až do 100,000. Áno, deMaroschko bol
naozaj výnimočný človek
môže byť až do 100,000. Áno, deMaroschko bol
naozaj výnimočný človek
Príklad
Vstup
N = 3 M = 5
1 3 4 1
3 5 7 2
4 6 5 3
1 4
2 3
4 3
5 2
5 4
Výstup
0
1
3
1
2