• KSP
• • Home
  • Novinky
  • Pravidlá
  • FAQ
  • Kuchárka
  • Liaheň
• Séria
• • Zadania a výsledky
  • Odovzdaj riešenie
  • Ideálne riešenie
  • Archív zadaní
  • Zbierka
• Akcie
• • Sústredenia
  • Proboje
  • Akadémia a klub
  • LTT
• Ostatné
• • Podporte nás
    2% z daní
  • Organizátori
  • Sponzori
  • Kontakt
• Iné semináre
• • Trojsten
  • KMS
  • FKS
  • Iné súťaže

Príklady 1. kola letnej časti 20. ročníka KSP

Milé naše riešiteľky, mílí naši riešitelia,

dostávajú sa vám do rúk zadania letnej časti XX. ročníka KSP. Prečítajte si pozorne propozície súťaže a hor sa riešiť. V prípade, že riešite KSP po prvý raz, odporúčame vám začať s kategóriou KSP-Z. Svoje riešenia nám posielajte najneskôr do 21. apríla 2003. Nezabudnite k nim priložiť známky v hodnote 15,- Sk.

1. O snaživom Tomášovi II
2. O dovolenke
3. O obchodnom cestujúcom
4. O Miškovi na ľade II
5. O celulárnych automatoch III

---

1. O snaživom Tomášovi II

(15 bodov)

Keď bol Tomáš ešte mladší a chodil do školy, bol známy tým, že chodil na veľa prednášok. Dokonca sa so svojim problémom dostal aj do zadaní KSP.

Teraz je Tomáš už starší, ale snaživý je stále. Keď dostal v práci deň voľna, rozhodol sa, že si zarobí na brigádach. Už mu nejde o to, aby ich stihol čo najviac, ale o to, aby si čo najviac zarobil. Peniaze za brigádu však dostane iba ak bude na celej brigáde.

Úloha

Na vstupe je zadané N – počet brigád, ktoré sa v ten deň konajú. Nasleduje N riadkov, každý z nich popisuje jednu brigádu. Popis brigády obsahuje 3 celé čísla s_i, t_i, c_i, kde s_i je čas začiatku brigády, t_i je čas jej konca a c_i je suma, ktorú si na nej môže Tomáš zarobiť. Ak jedna brigáda začína v rovnakom čase ako druhá končí, stíha obe.

Vašou úlohou je vypísať koľko najviac si môže Tomáš zarobiť, ak si vhodne vyberie brigády, na ktoré pôjde.

Príklad

Vstup
N=5,
brigády: (3,5,7), (5,8,6), (2,6,10), (6,7,5), (1,4,6)

Výstup
15

(Pôjde na brigády 3, 4.)

---

2. O dovolenke

(15 bodov)

Santo a Banto sa rozhodli, že pôjdu na dovolenku. A najradšej by išli niekam veľmi ďaleko. Zobrali si teda mapu a začali plánovať. Na tej mape sa dozvedeli kopu zaujímavých vecí. Napríklad zistili, že celý svet je vlastne kváder s dĺžkou M, šírkou N a výškou K, ktorý sa skladá z MxNxK kociek. Každá kocka obsahuje buď zem alebo vzduch. (S prekvapením zistili, že more neexistuje.) Pochopiteľne, pod kockou so zemou už nie sú žiadne kocky so vzduchom. Navyše pod celým svetom je zem.

Keď už našli miesto, ktoré je dosť ďaleko, uvedomili si, že ak sa tam nedostanú, neužijú si žiadnu dovolenku. A to nie je také jednoduché, lebo tak ďaleko sa dostane len málo dopravných prostriedkov. Zistili, že jediná možnosť je použiť vrtuľník. Tým sa ale ich problémy nekončia. Nevedia totiž, či im na takú dlhú cestu (a prípadne aj návrat) vystačí palivo. A boli by radi, keby im ostalo aj na ďalšiu dovolenku. Chceli by teda letieť tak, aby spotrebovali čo najmenej paliva. S tým sa im už ale nechce zaoberať a tak požiadali o pomoc vás.

Úloha

Vrtuľník môže letieť

• hore, z kocky so súradnicami (x,y,z) na kocku so súradnicami (x,y,z+1), spotrebuje pri tom a objemových jednotiek (OJ) paliva,
• dole, z kocky (x,y,z) na kocku (x,y,z-1), spotrebuje pri tom b OJ paliva,
• nabok, z kocky (x,y,z) do (x+1,y,z), (x-1,y,z), (x,y+1,z) alebo (x,y-1,z), spotrebuje c OJ paliva.

Samozrejme letieť sa dá len po vzduchu.

Sú dané prirodzené čísla M, N, K, a, b, c a výšková mapa sveta, čiže matica prirodzených čísel rozmerov MxN, pričom ak je v i-tom riadku a j-tom stĺpci hodnota v_ij, znamená to, že kocky na súradniciach (i,j,0) až (i,j,v_ij) obsahujú zem a tie na súradniciach (i,j,v_ij+1) až (i,j,K) obsahujú vzduch. Ďalej sú dané súradnice kociek A, B. Úlohou je nájsť cestu z kocky A do kocky B, pri ktorej sa spotrebuje čo najmenej paliva. Ak takých ciest existuje viac, nájdite ľubovoľnú z nich.

Príklad

Vstup
N=2, M=5, K=7 a=10, b=5, c=3 krajina:

4 4 4 3 2        
4 5 4 3 2        

A=(2,1,5) B=(2,5,3)

Výstup
(2,1,5), (1,1,5), (1,2,5), (1,3,5), (2,3,5), (2,4,5), (2,4,4), (2,5,4), (2,5,3)

---

3. O obchodnom cestujúcom

(15 bodov)

Pán Hamilton je obchodný cestujúci. Má taký veľký hnedý kufor a v ňom kopec vecí, ktoré by si niekto mohol kúpiť. A s týmto kufrom cestuje po svete a koho stretne, tomu ponúka čokoľvek, čo vo vnútri nájde.

Tak sa raz stalo, že sa objavil na Kiribati. Ako iste viete, Kiribati je súostrovie, do ktorého patrí veľa maličkých ostrovov. Vzhľadom na to, ako veľmi sú jednotlivé ostrovy od seba vzdialené, môžeme ich považovať za bodky. Pán Hamilton si v hlavnom prístave (kam doplával zaoceánskym parníkom) požičal motorový čln. Má totiž v pláne obehať všetky ostrovy (veď čo by to bol za obchodného cestujúceho, keby nenavštívil každý kút sveta), no nie hociako, ale každý ostrov práve raz (veď čo by to bol za obchodného cestujúceho, keby šiel predávať rovnaký tovar dvakrát na to isté miesto). Na tento plán by motorový čln mohol postačiť. Ale taký motorový čln spotrebuje hojne nafty, a tá je stále drahšia a drahšia, a preto sa musí jednak poponáhľať, ale hlavne musí zistiť, aká dlhá bude jeho cesta. Ak by totiž cesta bola príliš dlhá, nafta ho bude stáť viac bubákov, ako pri sebe má. Ako tak dumá nad problémom, priplietol sa mu do cesty ochotný deduško. Deduško mu hneď prezradil, že ostrovy ležia vo vrcholoch mysleného konvexného $N$-uholníka. Okrem toho deduško sľúbil, že mu povie vzdialenosť medzi ľubovoľnými dvoma ostrovmi. Pán Hamilton zdvorilo poďakoval, ale napriek tejto neočakávanej pomoci si nevie rady. Pomôžte mu, možno vám potom niečo dá zo svojho kufra.

Úloha

Na vstupe je daný počet ostrovov N, N\ge 3. Napíšte program, ktorý zistí dĺžku najkratšej trasy, ktorá prechádza každým ostrovom práve raz a začína aj končí na ostrove 1. Pre účely úlohy môžete spolu s Kiribatčanmi predpokladať, že Zem je rovná plocha. Deduškovi (užívateľovi) môžete dávať otázky typu Aká je vzdialenosť medzi ostrovmi A a B? a on vám pravdivo odpovie. Vzdialenosť môže byť iba kladné reálne číslo.

Príklad

Vstup
N=4

Aká je vzdialenosť medzi 1 a 2?
> 3.16228
Aká je vzdialenosť medzi 1 a 3?
> 2.0
Aká je vzdialenosť medzi 1 a 4?
> 2.82843
Aká je vzdialenosť medzi 2 a 3?
> 4.24264
Aká je vzdialenosť medzi 2 a 4?
> 3.16228

Výstup
Trasa má dĺžku 10.32

(Ostrovy tvoria vrcholy deltoidu so stranami 2 a sqrt(10), pričom kratšie dve strany zvierajú pravý uhol. Trasa vedie postupne cez ostrovy 1, 2, 4, 3.)

---

4. O Miškovi na ľade II

(15 bodov)

Zima už pomaly končí a Miško sa ešte stále poriadne nenaučil korčuľovať. Už sa naučil, že dobre sa korčuľuje len na ľade, z ktorého je odhrnutý sneh. No ako na potvoru, minulú noc snežilo a keď Miško prišiel k jazeru, zistil, že je celé zasnežené. Iba od brehu niekto kde-tu odhrnul kúsok ľadu. Miško sa však zatiaľ naučil korčuľovať iba na obdĺžnikovom klzisku (Nesmejte sa! To je tým, že zatáčať sa mu ešte príliš nedarí...), preto by si chcel nájsť nejaký odhrnutý kus ľadu v tvare obdĺžnika. A samozrejme čím väčší, tým lepšie.

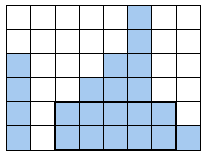
Úloha

Jazero má tvar obdĺžnika, ktorého spodná strana má dĺžku N metrov. Od tejto strany je poodhŕňaný sneh. Na prvom riadku vstupu je celé číslo N. Na druhom riadku je N celých čísel a₁, a₂, ..., a_N, pričom a_i udáva, pokiaľ je odhrnutý sneh pri i-tom metri brehu jazera. Nájdite obdĺžnik odhrnutého ľadu, ktorý má zo všetkých možných najväčší obsah. Na výstup vypíšte jeho plochu.

Príklad

Vstup
N=8

4 0 2 3 4 6 2 1

Výstup
10

(Obdĺžnik začína pri 3. metri brehu, končí pri 7. a siaha 2 metre od brehu.)

---

5. O celulárnych automatoch III

(15 bodov)

Novým riešiteľom stručne vysvetlíme, čo vlastne celulárne automaty sú. Tí, ktorí ste riešili predchádzajúce série, môžete preskočiť až ku zadaniu súťažnej úlohy.

Celulárny automat je poskladaný z množstva rovnakých krabičiek. Každá krabička môže byť v jednom z konečne veľa stavov. Každú sekundu sa každá krabička pozrie na svoj stav a na stav okolitých krabičiek a podľa nich (a ničoho iného!) sa rozhodne, v akom stave odteraz bude. Všetky krabičky teda naraz zmenia svoje stavy na nové. Zmenu stavu krabičky v závislosti od získaných informácií vieme popísať predpisom, ktorý budeme volať prechodová funkcia. Táto funkcia je vlastne akýsi jednoduchý program, ktorý krabička vykonáva. Všetky krabičky budú vykonávať ten istý program.

Naďalej sa budeme zaoberať jednoduchou situáciou – naša sústava automatov bude tvorená N rovnakými automatmi, uloženými v jednom rade. Každý automat má teda 2 susedov, až na krajné dva, ktoré majú len jedného. Zavedieme špeciálny stav $, ktorý vidia krajné automaty ako stav ich chýbajúceho suseda. (Dohodnime sa, že automat nemôže nadobudnúť tento stav a teda sa tváriť, že tam nie je.)

Kvôli šetreniu miestom a zároveň lepšej prehľadnosti budeme časť prechodovej funkcie: "Ak môj ľavý sused je v stave U, ja som v stave V a môj pravý sused je v stave W, zmením stav na X" zapisovať zjednodušene UVW-> X. Stavy automatov v konkrétnej sekunde budeme zapisovať ako jeden reťazec, t.j. napr. zápis $A011AB$ znamená, že naša sústava má 6 automatov, najľavejší automat je v stave A, jeho sused je v stave 0, atď. Znaky $ predstavujú stavy, ktoré vidia krajné automaty. Tento zápis zdôrazňuje, že na prechodovú funkciu sa môžeme dívať ako na sadu prepisovacích pravidiel – každú sekundu si pre každý automat nájdeme to pravidlo prechodovej funkcie, ktoré "naň pasuje" a potom podľa týchto pravidiel všetkým automatom naraz zmeníme stavy.

Príklad

Nech sú na začiatku všetky automaty v stave 0, iba ľavý krajný v stave 2. Napíšme program, po ktorého skončení budú párne automaty v stave 0, nepárne v stave 1. Uvedomme si, že problém je v tom, že program musí fungovať bez ohľadu na to, koľko automatov budeme mať. Pritom žiaden automat nemá dosť pamäte na to, aby si pamätal svoje poradové číslo, lebo to môže byť ľubovoľne veľké.

Riešenie môže vyzerať nasledovne: stav 2 bude akýsi "signál", ktorý si budú automaty posielať doprava a bude "ofarbovať" automaty, po ktorých prechádza, striedavo 1 a 0.

V programe teda použijeme 3 stavy: 0, 1 a 2. Prechodová funkcia bude vyzerať nasledovne:
$2x --> 1 pre x z množiny {0,$}, (prvý automat má mať stav 0)
20x --> 2 pre x z množiny {0,$}, (signál ide doprava)
x2y --> z pre x z množiny {0,1}, z=1-x, y z množiny {0,$}, (prišiel signál, zmením stav na opačný ako má sused)
x2$ --> z pre x z množiny {0,1}, z=1-x, (prišli sme na koniec)
xyz --> y pre všetky ostatné trojice stavov, (inak sa nič nedeje)

Ukážeme si výpočet našej sústavy na vstupe 20000 (t.j. 5 máme automatov):
$20000$ ==> $12000$ ==> $10200$ ==> $10120$ ==> $10102$ ==> $10101$ a v tomto stave už naša sústava zostane.

Úloha

Nech sú na začiatku všetky automaty v stave 0, iba ľavý krajný v stave Z (začiatok). Určte (konečnú!) množinu stavov automatu a napíšte prechodovú funkciu tak, aby niekoľko taktov po spustení prešiel stredný automat (ak ich je párny počet, oba stredné automaty naraz) do stavu S (stred). Žiaden iný automat nesmie počas výpočtu tento stav nadobudnúť. Snažte sa, aby bola dĺžka výpočtu vašej sústavy (v závislosti od počtu automatov) čo najmenšia.

Teda ak spustíme napr. sústavu 6 automatov, mala by zo stavu $Z00000 prejsť na niekoľko krokov do stavu $abSScd$ (pre nejaké a,b,c,d<>S).

Nezabudnite, že pri písaní prechodovej funkcie neviete, koľko vašich automatov vedľa seba naskladáme. Sústava zložená z ľubovoľného počtu vašich automatov by mala fungovať podľa zadania.

Pri návrhu prechodovej funkcie vám môže (a nemusí) pomôcť program, simulujúci sústavu vašich automatov. Ak si aj takýto program napíšete, neposielajte nám ho. Ako riešenie stačí poriadne popísaná množina stavov a prechodová funkcia vášho automatu. Ak to pomôže prehľadnosti vášho riešenia, stavy nemusíte značiť iba písmenami, napr. L₄₇' je skvelý názov pre stav.

Hint

Existuje ľahké riešenie s časom kvadratickým od počtu automatov. Existuje však aj lepšie riešenie.

---

(c) 13. Marec 2002 webmaster

---