- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady 1. kola zimnej časti 25. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia,
Práve prišiel nový školský rok a s ním aj nový ročník KSP. A ako to už s novými ročníkmi býva, bývajú vtedy aj prvé zadania. A tak aj tento rok prišli pekne zabalené v tomto letáčiku, tak si ich poriadne prečítajte, riešte, nech sa dostanete na jarné sústredenie...
Pevne veríme, že sa pustíte do riešenia úloh, ktoré sme pre vás pripravili. Nezabúdajte, že najlepších čaká pozvánka na sústredko, a tých ešte lepších čakajú aj nejaké tie knižné ceny.
Termín odoslania riešení tejto série je pondelok 15. októbra 2007. Riešitelia, ktorí sa za výsledky v minulom polroku dostali na jesenné sústredko, môžu riešenia odovzdať pri príchode na sústredko.
Kým nemáš aspoň kúsok salámy, tak po tebe ani papagáj neštekne.
KSPáci
- Zrátajme si jedničky
- Zajačia farma
- Zase tie preteky...
- O potápaní...
- Ooo, aký mocný odvar!
- Ohrozená posádka
- Ošemetná postupnosť
- O nekompromisnom Maroškovi
- Trápenie kráľa Artuša
- Táničkin tajomný trik
1. Zrátajme si jedničky
15 bodov, kategória Z
Jožko je veľmi šikovný a tak začal písať všetky čísla v dvojkovej sústave.
A navyše sa rozhodol, že jedničky bude písať červenou farbou a nuly čiernou.
Začal písať všetky čísla od 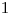 po
po 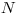 . Už mu chýba iba jedno, keď si tu zrazu
všimol, že sa mu míňa červená farba. Keby však vedel, koľko ešte jednotiek
napíše, tak by vedel, či mu pero vystačí, alebo či si má ísť kúpiť novú červenú
náplň. S týmto si však už nevedel poradiť, a preto sa obrátil na vás.
. Už mu chýba iba jedno, keď si tu zrazu
všimol, že sa mu míňa červená farba. Keby však vedel, koľko ešte jednotiek
napíše, tak by vedel, či mu pero vystačí, alebo či si má ísť kúpiť novú červenú
náplň. S týmto si však už nevedel poradiť, a preto sa obrátil na vás.
Úloha
Na vstupe dostanete číslo 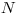 v desiatkovej sústave a vašou úlohou je vypísať
počet jedničiek potrebných na zápis tohto čísla v dvojkovej sústave.
v desiatkovej sústave a vašou úlohou je vypísať
počet jedničiek potrebných na zápis tohto čísla v dvojkovej sústave.
Príklad
Vstup
1025Výstup
22. Zajačia farma
15 bodov, kategória Z
Jožko sa raz rozhodol pestovať zajačiky. Kúpil si klietku a jeden utešený, čerstvo narodený pár zajačikov. Zajačiky boli hravé, rýchlo rástli, prešiel mesiac a Jožko si zmyslel, že keď sa zajačiky začnú rozmnožovať, po nejakom čase ich môže začať predávať a môže si celkom dobre zarobiť. Keď potenciálnym kupcom povie, aký výnos sa dá získať z jedného párika zajačikov, o kúpu isto nebude núdza. Tak si teda preventívne kúpil ešte jednu klietku a čakal. Čakal, prešiel druhý mesiac a dočkal sa. Na svet prišiel nový, utešený, čerstvo narodený pár zajačikov. Tak sa potešil, že mu to vychádza, že si kúpil aj tretiu klietku.
Prešlo niekoľko mesiacov, zajačiky sa množili (každý pár zajačikov privedie na svet každý mesiac počnúc druhým od svojho narodenia jeden pár zajačikov), množili, a Jožko im dokupoval nové a nové klietky, každý mesiac aspoň jednu.
Po čase ho navštívil bratranec Ferko. Keď mu Jožko ukázal zajačiky, Ferko s úžasom zhíkol: "Ale veď tvoje zajačiky sa rozmnožujú presne podľa Fibonacciho postupnosti!". "Ako to?", čudoval sa Jožko, ktorý asi ani netušil, čo tá Fibonacciho postupnosť je. "Každý mesiac predsa máš toľko párov zajačikov, ako si mal predchádzajúci mesiac plus koľko sa ich práve narodilo, a tých je toľko, koľko si mal pred dvoma mesiacmi, lebo len tí sa môžu rozmnožovať. A ako veľa klietok máš! Ako rozdeľuješ zajačiky do klietok?", spýtal sa ešte Ferko. "No, snažím sa byť spravodlivý a aby boli zajačiky čo najspokojnejšie, tak dávam do každej klietky rovnaký počet zajačikov", odvetil Jožko, len vtom ho prerušil Ferko: "No to ti celkom nesedí, spočítajme ich." A skutočne, v šiestich klietkach bolo po dvoch pároch, vo zvyšných troch boli až tri páry v každej. "Ale snažil som sa ich dať rovnako, len sa to nedalo! (nie, Jožko nebol až taký krutý) ", zúfalo nariekal Jožko. Ferkovi sa ho uľútostilo, tak si teda kúpil tie tri páriky, aby mu ostalo v každej klietke rovnako.
Úloha
Na vstupe je číslo 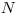 , ktoré vyjadruje počet mesiacov od kúpy prvého páru
zajačikov po príchod Ferka, potom nasleduje počet klietok
, ktoré vyjadruje počet mesiacov od kúpy prvého páru
zajačikov po príchod Ferka, potom nasleduje počet klietok 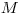 , do ktorých sa
Jožko práve pokúsil rovnomerne rozdeliť zajačiky. (Viete, že každý mesiac kúpil
aspoň jednu klietku, teda platí
, do ktorých sa
Jožko práve pokúsil rovnomerne rozdeliť zajačiky. (Viete, že každý mesiac kúpil
aspoň jednu klietku, teda platí 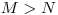 .) Vašou úlohou je vypísať počet zajačikov,
ktoré si Ferko od Jožka musí kúpiť, aby v každej klietke ostal rovnaký počet
zajačikov.
.) Vašou úlohou je vypísať počet zajačikov,
ktoré si Ferko od Jožka musí kúpiť, aby v každej klietke ostal rovnaký počet
zajačikov.
Formálne povedané, vypíšte zvyšok, ktorý dáva 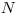 -té Fibonacciho číslo po delení
-té Fibonacciho číslo po delení 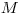 .
Fibonacciho postupnosť je taká postupnosť, v ktorej sa
.
Fibonacciho postupnosť je taká postupnosť, v ktorej sa 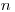 -tý člen rovná súčtu
predchádzajúcich dvoch. Formálne
-tý člen rovná súčtu
predchádzajúcich dvoch. Formálne 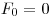 ,
, 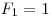 a
a 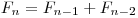 pre všetky
pre všetky 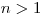 .
.
Príklad
Vstup
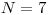 ,
, 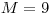
Výstup
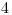
3. Zase tie preteky...
15 bodov, kategória Z
V Bantolande sa každý rok usporadúvajú cyklistické preteky, kde sa stretnú
najlepší cyklisti nielen z celého Bantolandu, ale dokonca aj zo Santolandu
(Bantoland aj Santoland boli pomenované po legendárnych zlatokopoch Bantovi a
Santovi). Tento rok to už bude 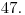 ročník týchto pretekov, a preto sa starosta
Bantolandu rozhodol, že spraví preteky čo najdlhšie možné (navyše, čím dlhšie
preteky, tým viac peňazí z nich získa). Keď sa však pozrel na mapu Bantolandu,
zistil, že to nebude také jednoduché. Totiž Bantoland pred rokom prešiel menšou
prestavbou a zrušili sa všetky zbytočné ulice.
ročník týchto pretekov, a preto sa starosta
Bantolandu rozhodol, že spraví preteky čo najdlhšie možné (navyše, čím dlhšie
preteky, tým viac peňazí z nich získa). Keď sa však pozrel na mapu Bantolandu,
zistil, že to nebude také jednoduché. Totiž Bantoland pred rokom prešiel menšou
prestavbou a zrušili sa všetky zbytočné ulice.
Ako teda Bantoland vyzerá?
V Bantolande je práve 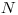 domov. Medzi domami vedie práve
domov. Medzi domami vedie práve
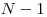 ulíc. Každá ulica spája (obojsmerne) práve dva domy.
Zároveň máte zaručené, že po uliciach sa dá (práve jedným spôsobom)
dostať od každého domu ku každému inému domu. Matematicky môžeme
povedať, že ulice v Bantolande tvoria strom.
ulíc. Každá ulica spája (obojsmerne) práve dva domy.
Zároveň máte zaručené, že po uliciach sa dá (práve jedným spôsobom)
dostať od každého domu ku každému inému domu. Matematicky môžeme
povedať, že ulice v Bantolande tvoria strom.
Cyklistická trať má začínať aj končiť pri nejakom dome a nesmie ísť dvakrát po tej istej ulici, aby sa cyklisti nepozrážali. Starosta Bantolandu by rád našiel takú trasu, ktorú tvorí čo najviac ulíc.
Úloha
Na vstupe dostanete číslo 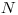 , ktoré udáva počet domov v Bantolande
(domy sú očíslované od
, ktoré udáva počet domov v Bantolande
(domy sú očíslované od 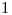 po
po 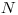 ). Ďalej nasleduje
). Ďalej nasleduje 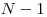 riadkov. Každý
obsahuje dve čísla
riadkov. Každý
obsahuje dve čísla 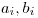 , čo sú čísla domov, medzi ktorými vedie ulica.
Ulice sa stretávajú len pri domoch, nikde inde sa nekrižujú.
Vašou úlohou je nájsť jednu takú trasu pretekov, ktorá obsahuje
čo najväčší počet ulíc. Vypíšte čísla domov v poradí, v akom na nájdenej
trase ležia.
, čo sú čísla domov, medzi ktorými vedie ulica.
Ulice sa stretávajú len pri domoch, nikde inde sa nekrižujú.
Vašou úlohou je nájsť jednu takú trasu pretekov, ktorá obsahuje
čo najväčší počet ulíc. Vypíšte čísla domov v poradí, v akom na nájdenej
trase ležia.
Príklad
Vstup
8 1 2 1 3 1 4 2 5 5 6 6 7 8 2Výstup
3 1 2 5 6 74. O potápaní...
15 bodov, kategória Z a O
"Zabetónovať a do Dunaja hodiť!" zreval Vojto. "Nieeee, veď to nemôžete!" zľakol sa chudák Wassil, ale už bolo neskoro. Jeho kanojku už prepadla flotila matfyzákov, ktorí čakali len na to, aby mohli chudáka Wassila potopiť. "Vegetaaa (nemýľte si to s vendetou) !" zvolal Maják a pádloval chudákovi Wassilovi na pomoc. Avšak, kanojka s Ondráčom mu zavadzala a tak sa rozhodol, že ju cestou potopí. Môže ju však potopiť? Nie sú náhodou v aliancii?
Ako je to s alianciami? Začalo to celé vtedy, keď sa Ondráč so Škrečkom
dohodli, že sa nebudú navzájom na lodičkách obracať. Keď to ale videla Ika s
Lenkou, tak sa dohodli tiež. A potom aj Mic s Miňom. Zatiaľ to bolo jednoduché.
Ale potom sa pridal Maty s Majákom, Wassil s Majákom, Maty s Micom... A
tu vzniká problém. Maják už vôbec netuší, kto s kým je v aliancii. Zvlášť
preto, lebo sa dodržuje pravidlo "Nepotopím toho, čo nepotopí toho, čo
nepotopí mňa (kamarát môjho kamaráta je môj kamarát) ". Formálnejšie
povedané, ak človek 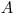 je v aliancii s človekom
je v aliancii s človekom 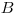 , tak je aj v aliancii so
všetkými, s ktorými je v aliancii človek
, tak je aj v aliancii so
všetkými, s ktorými je v aliancii človek 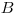 .
.
Maják je už s toho úplne zúfalý a nevie čo robiť. Preto požiadal o pomoc vás, aby ste mu vymysleli spôsob, ako rýchlo zistiť, s kým je kto v aliancii a zároveň aby sa vedel vysporiadať aj s rozširovaním aliancií.
Úloha
Na vstupe dostanete čísla 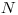 ,
, 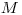 , kde
, kde 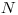 udáva počet ľudí a
udáva počet ľudí a 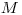 počet udalostí.
Ďalej nasleduje
počet udalostí.
Ďalej nasleduje 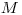 riadkov. Každý z nich popisuje jednu udalosť a obsahuje 3
čísla
riadkov. Každý z nich popisuje jednu udalosť a obsahuje 3
čísla 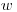 ,
, 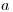 ,
, 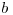 . Ak
. Ak 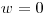 tak to znamená, že ľudia s číslami
tak to znamená, že ľudia s číslami 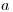 a
a 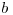 vytvorili
alianciu. Ak
vytvorili
alianciu. Ak 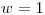 tak to znamená, že Maják chce vedieť, či ľudia
tak to znamená, že Maják chce vedieť, či ľudia 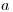 a
a 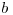 sú
spolu v aliancii. A pamätaj, že na začiatku nikto s nikým nie je v aliancii a
že Maják chce spracovávať všetky udalosti čo najrýchlejšie.
sú
spolu v aliancii. A pamätaj, že na začiatku nikto s nikým nie je v aliancii a
že Maják chce spracovávať všetky udalosti čo najrýchlejšie.
Príklad
Vstup
4 7 0 1 2 0 3 4 1 1 4 1 1 2 0 1 3 1 1 4 0 2 4Výstup
Nie Ano Ano5. Ooo, aký mocný odvar!
15 bodov, kategória Z a O
V miestnosti sa rozliehalo ticho a tma, len blikotajúci plameň v krbe raz za čas prezradil čo-to o zvyšku izby. Za stolom sa matne črtá postava starého čarodejníka a obrovského množstva malých fľaštičiek. Obyčajný človek by čakal nápisy ako "odvar z hadích uší" alebo "sušené netopierie plutvy". Avšak každý poriadny čarodejnícky učeň vie, že takéto označenia sa používajú iba v rozprávkach. Nič totiž nehovoria o prapodstate každého odvaru – o jeho sile.
Podľa Katalógu Strašidelných Pomôcok preto musí byť každý odvar označený číslom, ktoré hovorí o jeho mocnosti – štandardizovanej jednotke sily. Mocnosť odvaru je prirodzené číslo.
Navyše, prakticky každý čarodejník raz za čas svoje odvary riedi. Riedenie odvarov nie je jednoduchá vec, navyše sa pri ňom znižuje mocnosť. Takýto odvar sa nazýva tiež "odmocnený". Navyše, ak sa odmocnený odvar riedi druhý raz, získame "odmocnenejší". Ďalšie riedenia už nemajú zmysel, pretože sila odvaru sa tým už úplne stratí.
Niekedy sa hodí vedieť navzájom porovnať silu odvarov – aspoň sa
čarodejníci v krčme môžu chváliť, aké premocné odvary majú skryté v skrini.
Na to sa používa tzv. absolútna mocnosť. Pre obyčajný odvar je rovná jeho mocnosti,
pre odmocnený je to 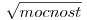 a pre odmocnenejší to je
a pre odmocnenejší to je 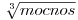 .
.
Úloha
Čarodejníkom sa tiež raz za čas zíde mať prehľad o tom, aké odvary vlastne majú – a to sa najlepšie robí tak, že si ich zoradia od najmenšej po najväčšiu absolútnu mocnosť. Čarodejníci ale nemajú radi zbytočne komplikované veci (však napokon preto sa zbavovali dlhočizných názvov odvarov) a rozhodne nechcú pri rátaní absolútnych mocností ani počuť o desatinných číslach.
Na vstupe máte dané číslo 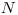 (počet odvarov) a
(počet odvarov) a 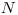 dvojíc čísel
dvojíc čísel 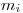 a
a
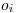 , kde
, kde 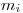 je mocnosť
je mocnosť 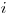 -teho odvaru a
-teho odvaru a 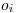 je
je 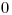 , ak je neriedený,
, ak je neriedený, 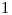 ak je odmocnený a
ak je odmocnený a 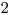 ak je odmocnenejší. Vašou úlohou je vypísať na výstup
tieto hodnoty utriedené podľa absolútnej mocnosti od najmenšej po najväčšiu.
Pokiaľ majú dva odvary rovnakú absolútnu mocnosť, zoraďte ich počnúc najviac
odmocneným.
ak je odmocnenejší. Vašou úlohou je vypísať na výstup
tieto hodnoty utriedené podľa absolútnej mocnosti od najmenšej po najväčšiu.
Pokiaľ majú dva odvary rovnakú absolútnu mocnosť, zoraďte ich počnúc najviac
odmocneným.
Príklad
Vstup
4 2 1 3 0 1 0 9 2Výstup
1 0 2 1 9 2 3 06. Ohrozená posádka
15 bodov, kategória O
Loď sa otriasla po zásahu laserom a kajutou zaznelo: "Chewie, nastav kurz dva-sedem-jedna!". "Čo to preboha robíš? Že nejdeš priamo vletieť do toho poľa asteroidov?" kontroval jemný ženský hlas. Muž odvetil: "Boli by blázni ak by za nami leteli, nie?". Na jeho rečnícku otázku odpovedal droid: "Pane, pravdepodobnosť bezpečného preletu cez pás asteroidov je približne tritisíc sedemstodvadsaťjedna ku jednej.". "Ja sa ale pravdepodobnosťou neriadim. Poletím bližšie k tomu veľkému." Princezná sa preľakla: "Bližšie? Veď to je hotová samovražda!"
Sú len dve možnosti ako tento príbeh bude pokračovať. Buď to je hotová samovražda a loď sa zrazí s asteroidom, alebo majú šťastie a tesne ho minú. To ale závisí od rozmerov, pozície a rýchlosti lode a rozmerov a pozície asteroidu (ten sa našťastie nehýbe). Žiaľ droid to nedokáže zistiť, a preto táto úloha ostáva na vás.
Úloha
Napíšte program, ktorý zistí, či sa loď zrazí s asteroidom. Loď aj asteroid sú
reprezentované ako 2D konvexné mnohouholníky. Na vstupe je počet vrcholov
lode (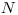 ), ich súradnice, počet vrcholov asteroidu
), ich súradnice, počet vrcholov asteroidu 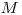 , súradnice týchto
bodov, a na koniec ešte dve čísla udávajúce vektor pohybu lode.
Vrcholy lode ani asteroidu nie sú uvedené v žiadnom konkrétnom poradí.
, súradnice týchto
bodov, a na koniec ešte dve čísla udávajúce vektor pohybu lode.
Vrcholy lode ani asteroidu nie sú uvedené v žiadnom konkrétnom poradí.
Príklad
Vstup
4 (1,1), (0,0), (0,1), (1,0) 4 (3,0), (3,1), (2,1), (2,0) (1,0)Výstup
Je to hotová samovražda!Vstup
3 (2,1) (3,3) (1,3) 3 (6,8) (10,8) (8,12) (1,2)Výstup
Uff, to bolo tesné!Vstup
6 (4,6) (3,5) (4,3) (6,4) (6,5) (3,4) 7 (10,11) (8,8) (9,7) (11,7) (14,9) (13,10) (7,10) (7,1)Výstup
Je to hotová samovražda!7. Ošemetná postupnosť
15 bodov, kategória O "A dá sa to!" "A nedá sa to!" "A predsa sa to dá!" ozývalo sa spoza dverí prednáškovej miestnosti. "Nedá sa to a nezdržiavaj ma s tým, za chvíľku mi začína prednáška," zaznelo rozhodne. Matfyzáci Jožko a Ferko strávili celé doobedie hádkou o probléme, ktorý našli napísaný na lavici. Jožko odvtedy tvrdí, že sa to vyriešiť dá a Ferko zase pravý opak. Jožko sa ale len tak ľahko nevzdáva a držiac sa Ferkovej poslednej vety do slova a do písmena, práve dotyčnú "chvíľku" využije na to, aby Ferkovi ukázal, že je schopný úlohu skutočne vyriešiť. Ale keďže času je málo, treba ju vedieť riešiť rýchlo. Veľmi rýchlo. A zároveň rátať s tým, že Ferko môže mať niekedy tiež pravdu.
Úloha
Zadanie napísané na lavici znelo nasledovne:
Pre dané 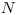 a
a 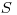 vždy existuje taká postupnosť celých čísel
vždy existuje taká postupnosť celých čísel
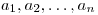 , pre ktorú platí
, pre ktorú platí
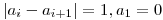 a zároveň
a zároveň
 .
.
Váš program má jednu takúto postupnosť nájsť a vypísať. Pokiaľ má pravdu Ferko a riešenie neexistuje, podajte o tom správu.
Príklad
Vstup
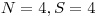
Výstup
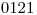
Vstup
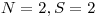
Výstup
Riešenie neexistuje.8. O nekompromisnom Maroškovi
15 bodov, kategória O a T
Možno si ešte pamätáte Maroška (Pripomíname, že ide o citovo zafarbenú verziu mena Maroš, nie Marek!) a jeho problém s knižnicou z predminulej série. Vďaka vaším programom sa jeho vzťahy s okolitým svetom výrazne zlepšili. Keď sa o nejaký čas Maroško rozhodol kandidovať na starostu svojej rodnej obce Jaroslav pri Dunaji, nemal problém nájsť dostatočnú podporu medzi spoluobčanmi.
Samozrejme, Maroško netúžil po funkcii len preto, aby si mohol štyri roky váľať šunky za štátne peniaze. Rozhodol sa, že v obci urobí nekompromisné reformy. A prvé, čo určite bude treba zmeniť, je priveľký počet stravovacích zariadení. Veď v Jaroslave sa vzmáha obezita!
Sadol si teda do svojej starostovskej kancelárie a pozrel sa na mapu obce, kde mal zakreslené všetky reštaurácie, bufety a cukrárne. "Tieto dve sú príliš blízko. Zrušíme ich a nahradíme jednou presne v strede cesty medzi nimi." povedal si pri pohľade na plán. Týmto rozhodnutím spečatil osud zariadenia Lahôdky u Mica a Wassilova palacinkáreň. Ani po tejto zmene ho ešte stav Jaroslava neuspokojoval. Našiel preto ďalšiu dvojicu najbližších zariadení, tie zrušil a nahradil ich novým v strede cesty medzi nimi. Takto pokračoval, až kým neostala jedna jediná reštaurácia.
Náhle si uvedomil, že podobný program by možno mohli využiť aj v iných dedinách. Okamžite sa v ňom prebudila túžba po peniazoch a rozhodol sa, že taký napíše a predá starostom iných obcí. Chcel by ale, aby program fungoval rýchlo. A keďže vôbec nevie programovať, je to nad jeho sily. Preto musí poprosiť o pomoc Vás.
Úloha
Napíšte program, ktorý pre pozície zadaných 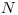 stravovacích zariadení
v dedine vypočíta, kde bude na konci stáť jediné, ktoré bude výsledkom postupu
it v každom okamihu zruším dve, ktoré majú k sebe najbližšie a nahradím ich jedným
v strede úsečky medzi nimi. V prípade, že v nejakom momente máte na výber viacero
dvojíc zariadení, medzi ktorými je rovnako dlhá cesta, spracujte tú dvojicu,
kde bude mať nové zariadenie najmenšiu
stravovacích zariadení
v dedine vypočíta, kde bude na konci stáť jediné, ktoré bude výsledkom postupu
it v každom okamihu zruším dve, ktoré majú k sebe najbližšie a nahradím ich jedným
v strede úsečky medzi nimi. V prípade, že v nejakom momente máte na výber viacero
dvojíc zariadení, medzi ktorými je rovnako dlhá cesta, spracujte tú dvojicu,
kde bude mať nové zariadenie najmenšiu 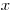 -ovú súradnicu. (Ak je ešte stále viac
možností, tak z nich vyberte tú, kde bude mať nové zariadenie najmenšiu
-ovú súradnicu. (Ak je ešte stále viac
možností, tak z nich vyberte tú, kde bude mať nové zariadenie najmenšiu 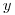 -ovú súradnicu.)
-ovú súradnicu.)
Príklad
Vstup
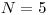
![[0,1],[4,0],[2,6],[8,4],[7,8]](obrazky/prikl8-4.png)
Výstup
![[4.75,4.625]](obrazky/prikl8-5.png)
Vstup
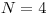
![[0,0],[2,0],[0,2],[3,3]](obrazky/prikl8-7.png)
Výstup
![[2,1.75]](obrazky/prikl8-8.png)
9. Trápenie kráľa Artuša
15 bodov, kategória T
Kráľ Artuš teraz prežíva obdobie najväčšej slávy. Jeho kráľovstvo prosperuje a má k dispozícii veľmi veľa kvalitných rytierov. S tým je však spojený jeden problém. Keďže rytierov je veľa, je veľmi nepravdepodobné, že by sa niekedy stretli naraz všetci za okrúhlym stolom. Situácia je však ešte komplikovanejšia. Niektorí rytieri sa nemajú radi a tak nemôžu sedieť pri okrúhlom stole vedľa seba.
Kráľ by teraz rád vedel, koho môže pozvať na najbližšie zasadnutie. Určite pozve nepárny počet rytierov, aby pri hlasovaní nemohla nastať remíza. Navyše vždy pozve viac ako jedného rytiera (teda aspoň troch).
Rytiera nazveme čierna ovca, ak ho Artuš nikdy nemôže pozvať na zasadnutie – inými slovami, ak neexistuje žiadny spôsob, ako pozvať tohoto rytiera spolu s nejakými ďalšími a usadiť ich za okrúhly stôl.
Úloha
Dané sú dve celé čísla 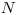 a
a 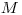 – počet rytierov a počet dvojíc rytierov,
ktorí sa nemajú radi. Nasleduje
– počet rytierov a počet dvojíc rytierov,
ktorí sa nemajú radi. Nasleduje 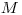 dvojíc
dvojíc 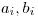 udávajúcich, že rytier
udávajúcich, že rytier
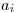 nemôže sedieť vedľa rytiera
nemôže sedieť vedľa rytiera 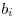 . Vašou úlohou je zistiť počet čiernych
ovcí medzi rytiermi – teda počet rytierov,
ktorých Artuš nebude môcť za žiadnych okolností pozvať na zasadnutie.
. Vašou úlohou je zistiť počet čiernych
ovcí medzi rytiermi – teda počet rytierov,
ktorých Artuš nebude môcť za žiadnych okolností pozvať na zasadnutie.
Príklad
Vstup
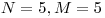 1 4
1 5
2 5
3 4
4 5
1 4
1 5
2 5
3 4
4 5
Výstup
2 Jediné platné rozsadenie tvoria rytieri 1, 2 a 3, preto sú rytieri 4 a 5 čierne ovce.10. Táničkin tajomný trik
15 bodov, kategória T
Táničke sa nedávno strašne zapáčilo prvočíslo 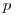 . Preto zanevrela
na klasickú aritmetiku a začala všetky operácie robiť modulo
. Preto zanevrela
na klasickú aritmetiku a začala všetky operácie robiť modulo 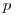 .
.
Nedávno si v škole na tabuľu napísala do kruhu 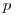 celých čísel.
Keď už ich všetky mala, zahľadela sa na ne, a nejak sa jej prestali
páčiť. Nuž zobrala znova do ruky kriedu. Prešla po obvode kruhu,
a medzi každé dve čísla napísala ich rozdiel. Potom všetky pôvodné
čísla zotrela.
celých čísel.
Keď už ich všetky mala, zahľadela sa na ne, a nejak sa jej prestali
páčiť. Nuž zobrala znova do ruky kriedu. Prešla po obvode kruhu,
a medzi každé dve čísla napísala ich rozdiel. Potom všetky pôvodné
čísla zotrela.
Teda napríklad ak
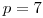 a pôvodne boli na tabuli čísla 3, 3, 1, 5, 3, 0 a 2, tak po
prepísaní budú na tabuli čísla
a pôvodne boli na tabuli čísla 3, 3, 1, 5, 3, 0 a 2, tak po
prepísaní budú na tabuli čísla 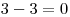 ,
, 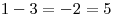 ,
, 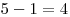 ,
,
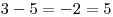 ,
, 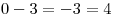 ,
, 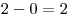 a
a 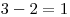 .
.
Tánička takto prepísala čísla na tabuli 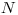 -krát, a potom odišla na obed.
Medzi časom prišiel do triedy jej starší brat Tomáš a niekoľko čísel
zotrel. Aké však bolo jeho prekvapenie, keď Tánička po príchode z obeda
všetky zotreté čísla správne doplnila späť!
-krát, a potom odišla na obed.
Medzi časom prišiel do triedy jej starší brat Tomáš a niekoľko čísel
zotrel. Aké však bolo jeho prekvapenie, keď Tánička po príchode z obeda
všetky zotreté čísla správne doplnila späť!
Úloha
Napíšte program, ktorý dostane na vstupe Táničkino prvočíslo 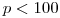 ,
počet prepísaní kruhu
,
počet prepísaní kruhu 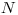 a postupnosť čísel, ktoré zostali na tabuli
po Tomášovom zásahu. Chýbajúce čísla budú nahradené otáznikmi. Môžete
predpokladať, že otáznikov je najviac
a postupnosť čísel, ktoré zostali na tabuli
po Tomášovom zásahu. Chýbajúce čísla budú nahradené otáznikmi. Môžete
predpokladať, že otáznikov je najviac 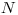 . Váš program by mal zistiť,
či sa dá z daných údajov jednoznačne nahradiť otázniky zmazanými
číslami. Ak je počet možností doplnenia rôzny od jednej, program by
o tom mal podať správu.
. Váš program by mal zistiť,
či sa dá z daných údajov jednoznačne nahradiť otázniky zmazanými
číslami. Ak je počet možností doplnenia rôzny od jednej, program by
o tom mal podať správu.
Príklad
Vstup
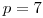 ,
, 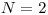 5 6 1 ? ? 6 6
5 6 1 ? ? 6 6
Výstup
5 6 1 6 5 6 6Táto postupnosť vznikne napr. dvoma prepísaniami postupnosti spomenutej v zadaní. Iné možnosti doplnenia neexistujú.
Vstup
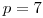 ,
, 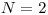 5 6 1 3 ? 6 6
5 6 1 3 ? 6 6

