- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady 2. kola zimnej časti 25. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia,
Prvé kolo ste úspešne poriešili a tak je čas na to, aby sa dostalo do povedomia aj druhé kolo zimnej časti KSP.
Nezabudnite, vidina jarného sústredenia možno časom nebude len vidinou. :-)
Pevne veríme, že sa pustíte do riešenia úloh, ktoré sme pre vás pripravili. Nezabúdajte, že najlepších čaká pozvánka na sústredko, a tých ešte lepších čakajú aj nejaké tie knižné ceny. A pre víťaza kategórie KSP-T okrem dobrej knižky aj nehynúca česť a sláva.
Termín odoslania riešení tejto série je pondelok 7. január 2008.
Vitaj, kto s dobrým úmyslom odchádzaš!
KSPáci
- Zradca?
- Zaspievajme si s vĺčkom
- Zase ten set...
- Zhodnotenie vedátorov
- Odhodlaná Anička
- Overená klebeta
- Otáčanie zátvoriek
- Okšoramove trampoty
- Ťažká matematika
- Tentokrát o grafe
1. Zradca?
15 bodov, kategória Z
Píše sa rok 1863, v USA zúri občianska vojna Sever proti Juhu. V Gettysburgu, malebnom mestečku v Pennsylvánii, sa schyľuje k bitke, ktorá má obrátiť doterajší priebeh vojny. Generál George nedával na hodinách dejepisu pozor, a preto nevie, ako sa tento boj skončí. A on by bol veľmi rád na strane víťazov, neváhal by kvôli tomu ani prejsť na stranu nepriateľa. Intuícia mu ale hovorí, že väčšiu šancu majú tí, ktorých je viac...
Úloha
Na začiatku vstupu je riadok obsahujúci čísla 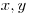 ,
ktoré určujú bojovú líniu – priamku idúcu cez body
,
ktoré určujú bojovú líniu – priamku idúcu cez body ![[0,0]](obrazky/prikl1-1.png) a
a ![[x,y]](obrazky/prikl1-2.png) .
Môžete predpokladať, že
.
Môžete predpokladať, že 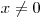 , teda bojová línia nejde priamo zo severu na
juh. Severom označíme tú polrovinu, kde leží bod
, teda bojová línia nejde priamo zo severu na
juh. Severom označíme tú polrovinu, kde leží bod ![[0,1]](obrazky/prikl1-4.png) ,
Juhom označíme druhú polrovinu.
,
Juhom označíme druhú polrovinu.
Nasleduje nepárne 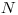 , čo je počet všetkých vojakov na bojisku. Potom nasleduje
, čo je počet všetkých vojakov na bojisku. Potom nasleduje
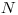 riadkov so súradnicami
riadkov so súradnicami 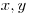 , určujúcimi polohu každého vojaka v teréne.
Môžete predpokladať, že žiaden vojak sa nenachádza priamo na bojovej línii.
Vašim cieľom je zistiť, či je viac vojakov na strane Severu alebo Juhu.
, určujúcimi polohu každého vojaka v teréne.
Môžete predpokladať, že žiaden vojak sa nenachádza priamo na bojovej línii.
Vašim cieľom je zistiť, či je viac vojakov na strane Severu alebo Juhu.
Príklad
Vstup
3 0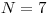 5 -3
6 1
8 3
7 -1
10 -2
12 1
47 47
5 -3
6 1
8 3
7 -1
10 -2
12 1
47 47
Výstup
George sa má pridať k Severu!Vstup
6 6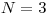 10 3
19 7
17 20
10 3
19 7
17 20
Výstup
George sa má pridať k Juhu!2. Zaspievajme si s vĺčkom
15 bodov, kategória Z
V minulom dieli ste videli: Vlkovi sa podarilo konečne dostať do domčeka kozliatok; než sa stihli poschovávať, mal ich všetky pekne v hrsti. Má veľkú hrsť. Keď bojuje, má sám zo seba strach. A šup kozliatko do pusy. Ani poriadne nepožul a už hltal ďalšie...
"Mňam... škoda, že ich bolo len sedem," povzdychol si vĺčok len čo zhltol posledné kozliatko. Tak moment! To piskľavé čudo, čo sa ozýva, má byť on? To nie je možné! Večer má predsa koncert s kapelou v lesnom kulturáku. Ako to zvládne? Veď sa mu úplne posunul rozsah. Nemôže v tom predsa medveďa so sysľom nechať, hrá s nimi už tri roky. Ale zároveň je mu jasné, že s týmto hlasom to neuspieva. Jedine ak by stihol všetky pesničky pre medveďa do večera transponovať (T. j. zmeniť ich tóninu, aby zneli vyššie/nižšie.) . Ale ako to stihnúť včas? No jasné, má ich predsa napísané v počítači. Stačí to zmeniť a znova vytlačiť. Ale kým to v tých textoch pohľadá všetko... a ešte aj vždy porátať, aký akord tam patrí... Jedine, že by mal na to program. Rýchlo treba zavolať kamarátke Ovečke, nech to stihne dať do najnovších zadaní KSP.
Úloha
Na vstupe je celé číslo 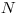 udávajúce o koľko poltónov chceme pesničku
transponovať. Ak je
udávajúce o koľko poltónov chceme pesničku
transponovať. Ak je 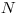 kladné, chceme transponovať nahor o
kladné, chceme transponovať nahor o 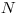 poltónov. V
prípade, že je
poltónov. V
prípade, že je 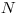 záporné, chceme transponovať nadol o
záporné, chceme transponovať nadol o 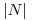 poltónov. Ďalej
je na vstupe text pesničky, v ktorom sú v hranatých zátvorkách vpísané
poltónov. Ďalej
je na vstupe text pesničky, v ktorom sú v hranatých zátvorkách vpísané
[akordy]. Môžete predpokladať, že zátvorky sa ako súčasť textu inak
nevyskytujú. (Dokiaľ nikto nezačne zhudobňovať skriptá z algebry.)
Výstup by mal obsahovať text pesničky v tom istom formátovaní, v akom je na
vstupe, pričom akordy v zátvorkách budú transponované o 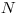 poltónov. A na
záver slovko k transpozícii. Akord je presne určený tónom na začiatku jeho
názvu. Ak chceme akord transponovať, musíme jeho tón zvýšiť alebo znížiť o
požadovaný počet poltónov. Pričom postupnosť tónov po poltónoch je (v
stúpajúcom poradí) C, C#, D, D#, E, F, F#, G, G#, A, B, H. Táto postupnosť
funguje cyklicky, čiže ak zvýšime H o poltón, dostaneme C, a naopak, ak znížime
C o poltón, dostaneme H. Akordové značky pre naše potreby budú vždy začínať
jedným z uvedených tónov a ľubovoľnou príponou (táto sa pri transpozícii
nemení).
poltónov. A na
záver slovko k transpozícii. Akord je presne určený tónom na začiatku jeho
názvu. Ak chceme akord transponovať, musíme jeho tón zvýšiť alebo znížiť o
požadovaný počet poltónov. Pričom postupnosť tónov po poltónoch je (v
stúpajúcom poradí) C, C#, D, D#, E, F, F#, G, G#, A, B, H. Táto postupnosť
funguje cyklicky, čiže ak zvýšime H o poltón, dostaneme C, a naopak, ak znížime
C o poltón, dostaneme H. Akordové značky pre naše potreby budú vždy začínať
jedným z uvedených tónov a ľubovoľnou príponou (táto sa pri transpozícii
nemení).
Príklad
Vstup
 J[D]si uz dlouho p[D#dim]ryc a nikdo b[Emi7]lizkej neni [Edim]nablizku,
pstr[Hmi]os je na tom l[F#mi]ip, ten muze st[G]rcit hlavu d[A]o pisku
a j[G]a ji strcim d[A]o okynka n[F#mi7]ejblizsiho t[Hmi7]axiku,
r[G]eknu: pane t[D]axikari, dv[G]akrat kolem r[A7]ovnik[D]u.[D#dim]
J[D]si uz dlouho p[D#dim]ryc a nikdo b[Emi7]lizkej neni [Edim]nablizku,
pstr[Hmi]os je na tom l[F#mi]ip, ten muze st[G]rcit hlavu d[A]o pisku
a j[G]a ji strcim d[A]o okynka n[F#mi7]ejblizsiho t[Hmi7]axiku,
r[G]eknu: pane t[D]axikari, dv[G]akrat kolem r[A7]ovnik[D]u.[D#dim]
Výstup
J[E]si uz dlouho p[Fdim]ryc a nikdo b[F#mi7]lizkej neni [F#dim]nablizku, pstr[C#mi]os je na tom l[G#mi]ip, ten muze st[A]rcit hlavu d[H]o pisku a j[A]a ji strcim d[H]o okynka n[G#mi7]ejblizsiho t[C#mi7]axiku, r[A]eknu: pane t[E]axikari, dv[A]akrat kolem r[H7]ovnik[E]u.[Fdim]3. Zase ten set...
15 bodov, kategória Z
Dvaja matfyzáci nedávno hrali sety. – Mám ho! Tu, tu a tu. – Nie, dva sú zelené a jeden červený. – Ktorý tubas kreslil tie kartičky? Veď zelená a modrá sa skoro vôbec nedá rozoznať! – Len ty ich nevieš rozoznať... SET! Tu, tu, tu. Cha! Už mám tretí. – Ďalší tu už nie je... – Počkaj chvíľu, podľa mňa tu ešte je, nájdem ho. – Naozaj nie je, viem to dokázať. Keď zoberieš len štvorce, šrafované tu nie sú, takže...
noindent Sety sa hrajú takto: Na stole sú karty, na každej sú nakreslené jeden až tri rovnaké symboly. Symbol má tri vlastnosti: farba, výplň a tvar. Každá vlastnosť môže nadobudnúť jednu z troch hodnôt:
- farba môže byť zelená, modrá, alebo červená
- výplň môže byť prázdna, šrafovaná, alebo plná
- tvar môže byť trojuholník, kruh, alebo štvorec
Každá karta má teda štyri vlastnosti. (kvízová otázka: ktorá je tá štvrtá?) Spolu je 81
rôznych kariet, pre každú kombináciu vlastností jedna.
Set je trojica kariet, pre ktorú platí, že každú vlastnosť majú buď všetky rovnakú alebo všetky
navzájom rôznu. Takže napríklad trojica jeden červený plný štvorec, dva modré šrafované kruhy, tri
zelené prázdne trojuholníky je set, lebo sa v každej vlastnosti líšia. Karty jeden modrý plný
kruh, dva zelené plné kruhy, tri červené plné kruhy tiež tvoria set.
Dá sa povedať, že trojica kariet nie je set, ak existuje
vlastnosť, ktorú majú dve karty rovnakú a tretia inú (viď rozhovor hore).
Matfyzákov už omrzeli klasické sety, preto si vymysleli vlastné lepšie. Namiesto 4 vlastností
a 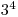 kariet majú matfyzné sety
kariet majú matfyzné sety 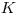 vlastností a
vlastností a 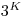 kariet. (Pre
kariet. (Pre  sa zvyknú
pridať vlastnosti: farba papiera, veľkosť objektov, hrúbka ťahu perom, vôňa, chuť, atď.))
sa zvyknú
pridať vlastnosti: farba papiera, veľkosť objektov, hrúbka ťahu perom, vôňa, chuť, atď.))
Úloha
Vstup začína číslom 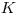 , ktoré udáva počet vlastností v setoch, ktoré ideme hrať.
Môžete predpokladať, že
, ktoré udáva počet vlastností v setoch, ktoré ideme hrať.
Môžete predpokladať, že 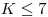 .
.
Ďalej je na vstupe daný počet kariet na stole 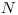 . Potom nasleduje
. Potom nasleduje 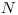 riadkov, ktoré obsahujú popis kariet.
Popis každej karty obsahuje
riadkov, ktoré obsahujú popis kariet.
Popis každej karty obsahuje 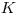 čísel z množiny
čísel z množiny 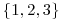 ,
predstavujúcich jednotlivé vlastnosti karty.
,
predstavujúcich jednotlivé vlastnosti karty.
Napríklad pre 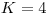 by tam boli štyri čísla
by tam boli štyri čísla 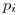 ,
, 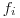 ,
, 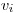 ,
, 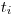 ,
pričom
,
pričom 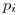 by bol počet objektov na
by bol počet objektov na 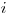 -tej kartičke,
-tej kartičke, 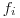 ich farba (
ich farba (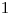 je zelená,
je zelená, 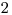 modrá a
modrá a
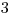 červená),
červená),
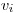 ich výplň (
ich výplň (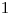 je prázdna,
je prázdna, 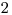 šrafovaná,
šrafovaná, 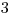 plná) a
plná) a 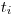 ich tvar (
ich tvar (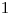 je trojuholník,
je trojuholník, 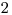 kruh a
kruh a 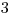 štvorec).
štvorec).
Váš program by mal čo najrýchlejšie spočítať, koľko je na stole takých trojíc kariet, ktoré tvoria set.
Príklad
Vstup
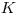 =4
=4
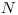 =6
3 1 1 1
2 2 3 2
1 3 2 3
3 1 3 2
3 3 2 3
2 3 2 3
=6
3 1 1 1
2 2 3 2
1 3 2 3
3 1 3 2
3 3 2 3
2 3 2 3
Výstup
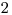 prvý set: 3 zelené prázdne trojuholníky, 2 modré plné kruhy, 1 červený šrafovaný štvorec
prvý set: 3 zelené prázdne trojuholníky, 2 modré plné kruhy, 1 červený šrafovaný štvorecdruhý set: 1, 2 a 3 červené šrafované štvorce
4. Zhodnotenie vedátorov
15 bodov, kategória Z a O
Náplňou práce takých vedátorov nie je len sedenie na akademických stoličkách na akademickej pôde a poznanie-rozširujúce vedátorovanie. Keď vedátor príde na nejaký svoj vedecký objav, rád sa oň podelí s vedeckou (či nevedeckou) obcou. (Najskôr sa podelí len tak opatrne s kolegami, zistí, že treba čo-to domyslieť; domyslí a potom už veselo publikuje.)
Niektorí vedátori sa o svoje objavy nedelia, ale ich priam násobia a stávajú sa z nich takí vedeckí pisálkovia. Nie vždy však kvantita znamená kvalitu. Dobrý vedátor je taký, ktorý napíše veľa dobrých článkov.
Ako ale spoznať, ktorý článok je dobrý? Jeden jednoduchý spôsob je pozrieť sa na počet citácii. Totiž keď vedátor píše článok, väčšinou sa v ňom odvoláva na iné, skôr napísané články, ktoré s tým jeho súvisia a ktoré on považuje za dobré. Preto môžeme zjednodušene povedať, že článok je tým lepší, čím viac iných článkov ho cituje. (Samozrejme, neráta sa, ak vedátor cituje v jednom svojom článku iný svoj článok.)
V roku 2005 prišiel Jorge Hirsch s nápadom, ako ohodnotiť produktivitu
a vplyv prác vedátorov. Zaviedol tzv.
h-index (http://en.wikipedia.org/wiki/Hirsch_number) :
Vedátor má h-index rovný 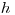 vtedy, keď:
vtedy, keď:
– napísal aspoň 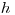 článkov, z ktorých každý má aspoň
článkov, z ktorých každý má aspoň 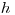 citácií
citácií
– každý z jeho ostatných článkov má najviac 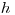 citácií
citácií
Úloha
Dokážte, že h-index vedátora je vždy určený jednoznačne.
Napíšte program, ktorý vypočíta h-index konkrétneho vedátora.
Na vstupe sú zadané čísla 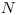 ,
, 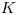 a
a 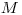 , kde
, kde 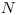 je počet článkov ktoré
berieme do úvahy,
je počet článkov ktoré
berieme do úvahy, 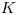 je počet článkov nášho vedátora a
je počet článkov nášho vedátora a 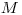 je celkový počet
citácií. Články sú očíslované od 1 do
je celkový počet
citácií. Články sú očíslované od 1 do 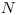 , pričom články 1 až
, pričom články 1 až 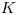 sú
články nášho vedátora.
Nasleduje popis citácií –
sú
články nášho vedátora.
Nasleduje popis citácií – 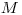 dvojíc čísel článkov, kde
dvojica
dvojíc čísel článkov, kde
dvojica 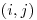 znamená, že článok
znamená, že článok 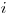 cituje článok
cituje článok 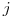 .
(Ak sa vám to hodí, môžete predpokladať, že medzi citáciami neexistuje cyklus.)
.
(Ak sa vám to hodí, môžete predpokladať, že medzi citáciami neexistuje cyklus.)
Príklad
Vstup
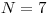 ,
, 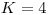 ,
, 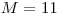 citácie:
5 1 1 2 6 2
6 5 4 2 7 4
3 6 7 1 7 6
6 1 9 2
citácie:
5 1 1 2 6 2
6 5 4 2 7 4
3 6 7 1 7 6
6 1 9 2
Výstup
2 (Článok 1 má tri citácie, článok 2 dve a článok 4 jednu. Máme teda 2 články, čo majú aspoň dve citácie.)5. Odhodlaná Anička
15 bodov, kategória Z a O
Keď sa naša kamarátka, emancipovaná Anička, naposledy prehŕňala u dedka Jonatána na povale, našla nádherný rodokmeň. Ten asi zostrojoval dedko pre ňu, lebo tam zapísal ju, jej rodičov a všetkých jej predchodcov, ktorých len vedel vypátrať. Samozrejme, vždy písal iba krstné mená. No a je verejne známe, že jej dedko je vášnivý informatik, a preto nebol rodokmeň zakreslený ako rozvetvený strom.
Jonatán rodokmeň zapisoval tak, že najprv zapísal všetkých predkov zo strany jej otca, potom zapísal Aničku a potom predkov zo strany jej mamy. No a keď zapisoval predkov z niekoho strany, tak vždy zapísal najprv predkov zo strany otca potom zapísal danú osobu a nakoniec predkov z maminej strany.
Anička si všimla, že ku každému menu si dedko napísal aj nejaké číslo. Po dlhšom skúmaní zistila, že dedko si ku každej osobe poznačil, koľko predkov zo strany otca pre tú osobu vypátral. To ju však veľmi zamrzelo. "Prečo práve zo strany otca? Typický mužský šovinizmus!". Rozhodla sa to za vašej pomoci zmeniť. Ku každej osobe zapíše, koľko predkov vypátral z maminej strany. Len to by najskôr zo zoznamu musela pochopiť, ako jej rodokmeň vlastne vyzerá.
Úloha
Na vstupe dostanete číslo 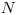 – počet členov rodiny, ktorých Jonatán vypátral.
Ďalej bude nasledovať rodokmeň pozostávajúci z
– počet členov rodiny, ktorých Jonatán vypátral.
Ďalej bude nasledovať rodokmeň pozostávajúci z 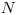 riadkov.
V každom riadku bude napísané meno osoby a počet jej predkov z otcovej strany, ktorí
sa nachádzajú v rodokmeni.
riadkov.
V každom riadku bude napísané meno osoby a počet jej predkov z otcovej strany, ktorí
sa nachádzajú v rodokmeni.
Vstup predstavuje rodokmeň jednej osoby 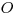 . Nemusí to byť Anička, program by mal fungovať
bez tohoto predpokladu. Vstup popisuje súvislú časť rodokmeňa, teda okrem osoby
. Nemusí to byť Anička, program by mal fungovať
bez tohoto predpokladu. Vstup popisuje súvislú časť rodokmeňa, teda okrem osoby 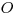 je
každý človek na zozname rodičom práve jednej inej osoby zo zoznamu.
Poradie osôb v zozname bolo určené postupom opísaným v zadaní.
je
každý človek na zozname rodičom práve jednej inej osoby zo zoznamu.
Poradie osôb v zozname bolo určené postupom opísaným v zadaní.
Vašou úlohou je vypísať tento zoznam tak, aby bol pri každom mene napísaný počet jej predkov z maminej strany, ktorí sa nachádzajú v rodokmeni.
Príklad
Vstup
10 Gustav 0 Karol 1 Fedor 0 Julia 1 Anicka 4 Jonatan 0 Alojza 1 Karol 0 Alzbeta 1 Beatrix 0Výstup
Gustav 0 Karol 2 Fedor 0 Julia 0 Anicka 5 Jonatan 0 Alojza 3 Karol 0 Alzbeta 1 Beatrix 0 (Toto je rodokmeň Aničky. Sú v ňom sú dvaja Karolovia. Anička je dcérou Karola a Alojzy. Karol je synom Gustáva a Júlie, ktorá ma otca Fedora. Alojza je dcérou Jonatána a Alžbety. Alžbeta je dcérou Karola a Beatrix.)6. Overená klebeta
15 bodov, kategória O
Veronika sa práve dozvedela skvelú overenú klebetu a musí ju čo najskôr povedať všetkým spolužiačkam. Nemôže čakať do zajtra, lebo vtedy už môže byť neskoro. Zdvihla telefón a už skoro vytočila meno prvej spolužiačky vo svojom zozname... keď vtom sa zarazila: "Ja vlastne chcem, aby všetci vedeli túto klebetu čo najskôr."
Rozširovanie klebety prebieha tak, že Veronika najprv zavolá jednej spolužiačke. Keď sa dorozprávajú, môže už klebetu rozširovať aj táto spolužiačka. Dĺžka hovoru dvoch spolužiačok závisí od toho, aké sú dobré kamarátky – musia predsa ešte rozobrať najnovšiu módu, kozmetiku...
Keďže je len pár dní po začiatku roka a Veronika práve nastúpila do prvej triedy, skamarátiť sa a vymeniť si čísla ešte stihlo len niekoľko dvojíc dievčat. Momentálna situácia v triede vyzerá tak, že klebeta sa síce vie dostať ku každej spolužiačke, ale pre každú spolužiačku existuje len jediný spôsob, ako sa klebeta môže dostať od Veroniky k nej. (Povedané matematicky, hrany "kto komu vie volať" tvoria strom.)
Úloha
Na vstupe je celé číslo 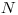 – počet dievčat v triede. Nasleduje
– počet dievčat v triede. Nasleduje 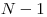 trojíc
trojíc
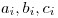 . Každá trojica hovorí, že chce jedno z dievčat s číslami
. Každá trojica hovorí, že chce jedno z dievčat s číslami 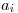 a
a 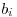 povedať
druhému klebetu, budú sa rozprávať
povedať
druhému klebetu, budú sa rozprávať 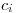 minút. Vašou úlohou je nájsť najmenší
možný čas, kedy budú klebetu poznať všetky spolužiačky. Veronika má číslo 1.
minút. Vašou úlohou je nájsť najmenší
možný čas, kedy budú klebetu poznať všetky spolužiačky. Veronika má číslo 1.
Príklad
Vstup
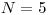 3 2 2
2 1 1
1 4 1
1 5 1
3 2 2
2 1 1
1 4 1
1 5 1
Výstup
3 Najprv zavolá spolužiačke 2. Potom v čase 1 spolužiačka 2 zavolá spolužiačke 3 a zároveň Veronika zavolá 4. V čase 2 Veronika zavolá spolužiačke 5. V čase 3 už vedia klebetu všetky.7. Otáčanie zátvoriek
15 bodov, kategória O
Keď bol Konrád malý, rád sa hrával so zátvorkami. Veľmi sa mu páčilo, že každá mala pár. A tak si aj spravil takú hračku. Vyzerala ako jeden veľmi dlhý pás, na ktorom boli samé zátvorky. Každá zo zátvoriek sa dala otočiť, čím sa zmenila z pravej na ľavú alebo naopak. Konrád si veľmi dával pozor, aby každá zátvorka mala svoj pár a veľmi sa vytešoval zo svojej hračky.
Ale jeho radosť netrvala dlho. Raz mu vypadla z rúk na zem a zátvorky sa mu všelijako poprehadzovali. A tak sa rozhodol, že to rýchlo dá do poriadku. Tak otočil prvú zátvorku a začal kontrolovať, či už je všetko správne uzátvorkované. To mu trvalo hodnú chvíľku. Potom otočil ďalšiu zátvorku... Asi po dvoch hodinách si uvedomil, že bude potrebovať pomoc. A tak sa obrátil na vás...
Úloha
Prvý riadok vstupu obsahuje dve čísla 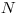 a
a 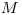 . Druhý riadok obsahuje reťazec
. Druhý riadok obsahuje reťazec
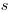 dĺžky
dĺžky 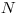 , ktorý sa skladá len zo znakov ( a ).
Nasledujúcich
, ktorý sa skladá len zo znakov ( a ).
Nasledujúcich 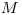 čísel
čísel  bude popisovať jednotlivé udalosti.
Ak je
bude popisovať jednotlivé udalosti.
Ak je 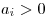 , tak sa na
, tak sa na 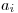 -tom mieste reťazca
-tom mieste reťazca 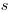 zmenila zátvorka.
Ak je
zmenila zátvorka.
Ak je 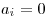 , treba vypísať ÁNO alebo NIE podľa toho, či je
reťazec
, treba vypísať ÁNO alebo NIE podľa toho, či je
reťazec 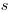 v danom momente korektne uzátvorkovaný.
v danom momente korektne uzátvorkovaný.
pojemKorektne uzátvorkovaný reťazec môžeme definovať nasledovne:
- () je korektne uzátvorkovaný reťazec.
- Ak
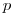 je korektne uzátvorkovaný reťazec, tak aj (
je korektne uzátvorkovaný reťazec, tak aj (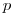 ) je korektne uzátvorkovaný
reťazec.
) je korektne uzátvorkovaný
reťazec.
- Ak
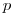 a
a 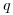 sú korektne uzátvorkované reťazce, tak aj
sú korektne uzátvorkované reťazce, tak aj 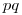 je korektne uzátvorkovaný reťazec.
je korektne uzátvorkovaný reťazec.
- Reťazec, ktorý nevieme takýmto postupom vyrobiť, nie je korektne uzátvorkovaný.
Príklad
Vstup
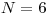 ,
, 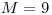 ()())(
0 5 0 6 0 1 0 1 0
()())(
0 5 0 6 0 1 0 1 0
Výstup
NIE NIE ÁNO NIE ÁNO8. Okšoramove trampoty
15 bodov, kategória O a T
Žabiak Okšoram sedí na svojom zaslúženom lekne plávajúcom na rybníčku a vychutnáva si pekný deň. Pokúša sa chytať mušky svojím mlsným jazýčkom. Dnešok má veľmi úspešný: spapal ich už niekoľko desiatok.
Náhle ale jesennú idylku prerušilo hysterické kŕkanie. Bolo to kŕkanie žabky alebo žabiačika, ktorému sa muselo stať niečo vážne. Okšoram sa rozhliadol a uvidel svojho kamaráta Akinoma, ako sedí o niekoľko lekien ďalej a narieka: "Stratil som svoj prsteň." Žabiak sa porozhliadol ešte raz a na inom lekne ďaleko od seba spozoroval Akinomov prsteň. Keďže Akinom je evidentne psychicky zrútený, musí mu Okšoram pomôcť. Vie totiž, ako veľa prsteň pre neho znamená. Je krásny, tajomne sa trbliece, vyrobený z najvzácnejších rias a ako ozdobu má malý snehovobiely leknový kvietok.
Okšoram skočil na vedľajšie lekno. To sa ale zatriaslo a začalo potápať. Mladý, ale veľký žabiak si uvedomil, že dneska veľmi pribral na váhe a žiadne lekno pod ním nie je schopné vydržať veľmi dlho. A odkedy ľudia pustili do rybníčka dravé šťuky, potopeniu alebo skoku do vody sa žabky vyhýbajú zo všetkých síl. Okšoram sa preto musí rýchlo rozhodovať. Čo je ale horšie, po skočení na nejaké lekno sa toto za chvíľu ponorí a už sa nebude dať použiť. Úloha sa mu komplikuje. Potrebuje preskákať k stratenému prsteňu a potom ho doniesť Akinomovi. Hodil by sa mu program, ktorý mu rýchlo poradí cestu, ale vôbec nevie algoritmicky programovať. Pomôžte chudákovi Okšoramovi!
Úloha
Na vstupe je počet lekien 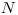 , očíslovaných od
, očíslovaných od 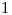 po
po 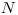 , ďalej
čísla troch významných lekien –
, ďalej
čísla troch významných lekien – 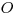 ,
, 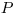 ,
, 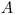 . Na
. Na 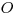 sedí Okšoram,
na
sedí Okšoram,
na 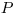 je stratený prsteň a na
je stratený prsteň a na 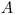 narieka Akinom.
Môžete predpokladať, že všetky tri významné lekná
sú rôzne. Nasleduje
narieka Akinom.
Môžete predpokladať, že všetky tri významné lekná
sú rôzne. Nasleduje 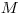 – počet rôznych možných skokov medzi leknami.
O každom skoku sú na vstupe čísla
– počet rôznych možných skokov medzi leknami.
O každom skoku sú na vstupe čísla 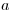 a
a 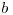 ktoré
hovoria, že z lekna
ktoré
hovoria, že z lekna 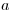 vieme preskočiť na lekno
vieme preskočiť na lekno 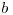 , a
aj symetricky z lekna
, a
aj symetricky z lekna 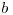 na lekno
na lekno 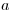 .
Vašou úlohou je nájsť a vypísať postupnosť lekien, po ktorých má Okšoram skákať, aby sa dostal k prsteňu a potom ho
bol schopný odniesť Akinomovi. Po každom skoku
sa opustené lekno potopí a všetky skoky z neho a na neho prestávajú
byť možné. Stačí nájsť ľubovoľnú možnú cestu. V prípade, že sa preskákať nedá, podajte o tom správu.
.
Vašou úlohou je nájsť a vypísať postupnosť lekien, po ktorých má Okšoram skákať, aby sa dostal k prsteňu a potom ho
bol schopný odniesť Akinomovi. Po každom skoku
sa opustené lekno potopí a všetky skoky z neho a na neho prestávajú
byť možné. Stačí nájsť ľubovoľnú možnú cestu. V prípade, že sa preskákať nedá, podajte o tom správu.
Príklad
Vstup
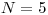 ,
, 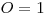 ,
, 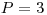 ,
, 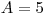 ,
,  1 2
1 5
2 3
2 5
3 4
4 5
3 5
1 2
1 5
2 3
2 5
3 4
4 5
3 5
Výstup
1 2 3 59. Ťažká matematika
15 bodov, kategória T
Možno to viete, možno nie, ale na matfyze je občas ťažké preliezť všetkými možnými podmienkami na zápočet, podmienkami na písanie skúškovej písomky, či pokračovanie do prvého (a potom aj druhého) teoretického kola skúšky.
Ferko si už na všetky tieto zvláštne podmienky zvykol, keď si len tak zo srandy zapísal Úvod do základov algebraickej teórie vyvažovania. Už len keby nebol ten ich prednášajúci profesor Hastea taký zvláštny...
Semester ubehol ako voda, a už tu bolo skúškové. Ferko sa teda chystá na skúšku (surfuje po internete na svojich obľúbených stránkach, hrá sa svoju obľúbenú hru a chatuje na jabberi), keď tu počuje dvoch svojich spolužiakov, ako sa bavia:
"Počul si, ako to vyzerá na skúške z ÚDZATV? Na skúške má také veľké dvojramenné váhy, so sadou závaží. Gramové, dvojgramové, štvorgramové... Až po 1024-gramové! Občas si ich donesie viac, občas menej. A vždy si donesie nejakú knihu. Dá ju na jednu stranu váh, a každý, kto chce písať skúškovú písomku, musí vyrovnať váhy. Ale nie hocijako, musí to spraviť inak ako študenti pred ním!"
"A sakra, to asi bude ťažké, však?"
"No, občas je dosť možností, lebo môžeš dávať závažia na obe strany váhy. Ale občas donesie málo závaží, alebo nejakú čudnú knihu... Ale nosí ich tam v poradí, v akom ich má v kancelárii. Zajtra si asi prinesie Červenú Algebru."
Ferko prestal dávať pozor a začal rozmýšľať, koľko študentov sa môže dostať ku skúške, ak by sme vedeli váhu knihy a počet závaží. Pomôžete mu?
Úloha
Mame číslo 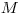 , označujúce hmotnosť knihy v gramoch, a počet závaží
, označujúce hmotnosť knihy v gramoch, a počet závaží 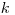 . Závažia majú hmotnosť
. Závažia majú hmotnosť
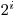 , pre
, pre  . Koľkými spôsobmi môžeme umiestniť závažia tak, aby vyvážili
knihu?
. Koľkými spôsobmi môžeme umiestniť závažia tak, aby vyvážili
knihu?
Príklad
Vstup
5 3Výstup
2 (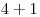 a
a 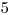 alebo
alebo 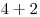 a
a 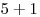 )
)
10. Tentokrát o grafe
15 bodov, kategória T
V kategórii T sa už na nič nehráme. Ani cesty, ani kamaráti. Obyčajný graf máme, čo si budeme navrávať.
Máme teda 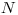 vrcholov. Niektoré dvojice vrcholov sú spojené hranou,
hrán je dokopy
vrcholov. Niektoré dvojice vrcholov sú spojené hranou,
hrán je dokopy 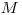 . V každom vrchole je nalepený papierik.
Na niektorých papierikoch je napísané celé číslo, ostatné sú
prázdne. Všetky celé čísla na papierikoch sú medzi
. V každom vrchole je nalepený papierik.
Na niektorých papierikoch je napísané celé číslo, ostatné sú
prázdne. Všetky celé čísla na papierikoch sú medzi 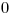 a
a 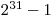 ,
vrátane.
,
vrátane.
Vašou úlohou bude dopísať čísla na ostatné papieriky tak, aby divnosť výsledného grafu bola najmenšia možná.
Aha, a že čo je to tá divnosť grafu? Pre každú hranu sa pozrieme na
papieriky na jej koncoch a spočítame bitový xor čísel na nich.
Takto dostaneme 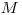 celých čísel, tie všetky dokopy sčítame
a výsledok je práve tá divnosť grafu, ktorá nás zaujíma.
celých čísel, tie všetky dokopy sčítame
a výsledok je práve tá divnosť grafu, ktorá nás zaujíma.
Úloha
Na vstupe je počet vrcholov 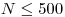 , počet hrán
, počet hrán 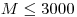 a počet
a počet 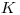 vrcholov, v ktorých už sú napísané čísla.
vrcholov, v ktorých už sú napísané čísla.
Nasleduje 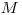 dvojíc čísel od 1 do
dvojíc čísel od 1 do 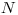 , ktoré popisujú hrany.
No a nakoniec je tam
, ktoré popisujú hrany.
No a nakoniec je tam 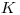 dvojíc čísel, udávajúcich číslo vrcholu
a číslo na jeho papieriku.
dvojíc čísel, udávajúcich číslo vrcholu
a číslo na jeho papieriku.
Vypíšte 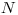 čísel, ktoré budú na konci na papierikoch. Ak je viac
riešení, vypíšte jedno ľubovoľné.
čísel, ktoré budú na konci na papierikoch. Ak je viac
riešení, vypíšte jedno ľubovoľné.
Príklad
Vstup
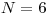 ,
, 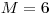 ,
, 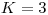 hrany:
hrany:
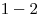 ,
, 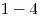 ,
, 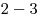 ,
,
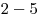 ,
, 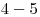 ,
, 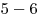 papieriky:
1 5
3 9
5 11
papieriky:
1 5
3 9
5 11

