- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady 1. kola letnej časti 25. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia, milé naše riešiteľatá,
Tak sa nám semester so semestrom zišiel a opäť sa vám dostávajú do rúk zadania Vášho obľúbeného semináru. Než si ale oslintáte klávesnicu pri vidine jesenného sústredenia dovolíme si Vás schladiť. Aby sa človek dostal na sústredenie, musí sa snažiť (tak aspoň znie oficiálne stanovisko) ! Preto dúfame, že sa rýchlo pustíte do riešenia týchto chrumkavých úloh, ktoré Vám naservírovali vaši obľúbení vedúci.
Aby ste holúbätká náhodou nenadobudli pocit, že to robíte nadarmo, pripomíname Vám, že najlepších čaká pozvánka na sústredko, a tých najlepších z najlepších navyše aj úžasné knižné ceny. A pre víťaza kategórie T samozrejme okrem knižnej odmeny aj nehynúca sláva, a dav rozvášnených fanyniek (KSP neručí, za žiadnu súčasť ceny s výnimkou knižnej) .
A dokedy toto všetko? Termín odoslania riešení tejto série je už pondelok 10. marca 2008.
P=NP? Hapciiii! Je to pravda...
KSPáci
- Zlietajú sa lastovičky
- Zmrznutá tybloň
- Zase tie výroky...
- Organizácia Kopanie Stôk Prievidza
- Opály, zafíry, a iné drahé kamene
- Obchod
- Ondrejova hra
- O televíznej hre
- Tóny ľubozvučných melódií
- – je v morzeovke T
1. Zlietajú sa lastovičky
15 bodov, kategória ZPrebúdza sa lúka, pole, prebúdza sa hora, zlietla zrána lastovička do nášho dvora.
Čo nevidieť tu bude jar a lastovičky sa k nám začnú vracať zo zimných krajín. Najviac ich môžeme vidieť sedávať pokope na drôtoch elektrického vedenia.
Avšak také lastovičky si nesadajú na tieto drôty náhodne. Aby sa pod nimi drôt náhodou neprehol, snažia sa nesadať si k sebe na vzdialenosť
menšiu ako 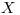 .
Vieme, že na našom drôte už nejaké lastovičky sedia. Chceme teraz zistiť, koľko sa
ich tam ešte zmestí.
.
Vieme, že na našom drôte už nejaké lastovičky sedia. Chceme teraz zistiť, koľko sa
ich tam ešte zmestí.
Úloha
Na vstupe máte zadaný počet lastovičiek 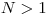 a minimálnu vzdialenosť dvoch
lastovičiek
a minimálnu vzdialenosť dvoch
lastovičiek 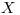 (kde
(kde 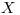 je celé číslo).
je celé číslo).
Ďalej nasleduje 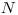 riadkov,
kde v
riadkov,
kde v 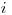 -tom riadku je zadaná pozícia
-tom riadku je zadaná pozícia 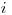 -tej lastovičky. Pozícia je
celé číslo, udávajúce vzdialenosť lastovičky od začiatku drôtu, na ktorom sedia.
Môžete predpokladať, že lastovičky sú zadané v poradí, v akom sedia
na drôte, a že žiadne dve nie sú k sebe bližšie ako
-tej lastovičky. Pozícia je
celé číslo, udávajúce vzdialenosť lastovičky od začiatku drôtu, na ktorom sedia.
Môžete predpokladať, že lastovičky sú zadané v poradí, v akom sedia
na drôte, a že žiadne dve nie sú k sebe bližšie ako 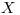 .
.
Vašou úlohou je vypísať, koľko najviac
lastovičiek si môže prisadnúť medzi prvú a poslednú lastovičku tak, aby
naďalej platilo, že vzdialenosť ľubovoľných dvoch lastovičiek je aspoň 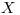 .
.
Príklad
Vstup
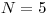 ,
, 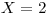 0
5
10
19
22
0
5
10
19
22
Výstup
5 (Sadnúť si môžu napr. na pozície 2, 8, 12, 15 a 17)2. Zmrznutá tybloň
15 bodov, kategória ZSanto je veľký pestovateľ tybĺk. (V skutočnosti pestuje tyblone, ale ako iste všetci viete, tyblká rastú na tybloniach.) Ako taká tybloň vyzerá? Zo zeme vyrastá kmeň. Na konci kmeňa sedí tyblko. Z tyblka vyrastajú (ale nemusia) ďalšie konáre. Na konci každého konára sedí ďalšie tyblko. Z tých tybĺk zase môžu vyrastať konáre, atď. Navyše v každom tyblku je malý, zlatý, päťkarátový červíček. Tyblone sa pestujú pre šupku tybĺk a pre červíčky. Avšak ak chceme vybrať z tyblka červíčka, musíme ho rozrezať (Rozrezať musíme samozrejme tyblko, nie červíka. A už vôbec nie Santa.) , čím sa poškodí šupka a navyše odpadnú všetky konáre, čo z neho rastú, aj so všetkým, čo je na nich. Červíci z odpadnutých tybĺk zdrhnú a teda sa dá predať iba ich šupka. Rozrezaním jedného tyblka teda získame jedného červíka (z neho) a niekoľko šupiek (z iných tybĺk, čo odpadli).
Santo sa rozhodol splatiť hypotéku, a tak začal rozmýšľať, koľko vie vlastne na tybloni zarobiť. Pre každé tyblko si zistil cenu jeho červíka a cenu jeho šupky. Teraz húta, ktoré tyblká rozrezať a ktoré predať na šupky – skúste mu pomôcť.
Úloha
Na vstupe je číslo 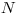 , ktoré označuje počet tybĺk. Tyblká sú očíslované od
, ktoré označuje počet tybĺk. Tyblká sú očíslované od
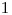 po
po 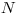 . Tyblko s číslom
. Tyblko s číslom 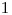 sedí na kmeni tyblone. Ďalej nasleduje
sedí na kmeni tyblone. Ďalej nasleduje
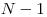 riadkov, každý z nich obsahuje
dve čísla tybĺk
riadkov, každý z nich obsahuje
dve čísla tybĺk 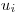 a
a 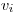 , ktoré sú spojené konárom.
Môžete predpokladať, že
medzi každými dvoma tyblkami existuje práve jedna cesta po konároch (a teda to
je strom). Na konci je ďaľších
, ktoré sú spojené konárom.
Môžete predpokladať, že
medzi každými dvoma tyblkami existuje práve jedna cesta po konároch (a teda to
je strom). Na konci je ďaľších 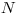 riadkov;
riadkov; 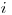 -ty z týchto riadkov obsahuje
dve čísla,
-ty z týchto riadkov obsahuje
dve čísla, 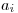 a
a 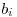 :
: 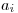 je cena šupky a
je cena šupky a 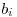 je cena červíka
z
je cena červíka
z 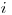 -teho tyblka.
-teho tyblka.
Santo postupne rozrezáva tyblká. V každom kroku si vyberie tyblko, ktoré
je ešte na tybloni, alebo sa rozhodne, že s rezaním končí.
Ak si vyberie 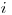 -te tyblko, rozreže ho a dostane
-te tyblko, rozreže ho a dostane 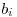 peňazí za červíčka
v ňom. Všetky vetvy vychádzajúce z tyblka odpadli a za každé tyblko
peňazí za červíčka
v ňom. Všetky vetvy vychádzajúce z tyblka odpadli a za každé tyblko 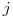 na odpadnutej vetve si Santo pripíše
na odpadnutej vetve si Santo pripíše 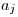 peňazí za šupku. Keď s rezaním
skončí, získa ešte
peňazí za šupku. Keď s rezaním
skončí, získa ešte 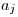 peňazí za šupku každého tyblko
peňazí za šupku každého tyblko 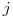 , ktoré ešte
zostalo na tybloni. Vašou úlohou je napísať program, ktorý vypočíta,
koľko peňazí vie Santo najviac zarobiť.
, ktoré ešte
zostalo na tybloni. Vašou úlohou je napísať program, ktorý vypočíta,
koľko peňazí vie Santo najviac zarobiť.
Príklad
Vstup
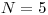 2 1
3 2
4 3
5 4
1 1
5 3
4 7
7 4
0 1
2 1
3 2
4 3
5 4
1 1
5 3
4 7
7 4
0 1
Výstup
21 Najskôr rozreže tyblko číslo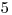 . Dostane
. Dostane 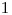 peniaz za červíka v ňom. Potom tyblko číslo
peniaz za červíka v ňom. Potom tyblko číslo 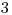 . Dostane
. Dostane 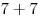 peňazí (
peňazí (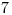 za červíka v tyblku číslo
za červíka v tyblku číslo 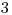 , a
, a 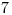 za šupku z tyblka
za šupku z tyblka 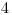 ). Nakoniec predá aj zvyšok stromu, za čo dostane
). Nakoniec predá aj zvyšok stromu, za čo dostane 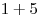 peňazí za šupky zo zvyšných tybĺk. Dokopy má teda
peňazí za šupky zo zvyšných tybĺk. Dokopy má teda 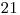 peňazí.
peňazí.
3. Zase tie výroky...
15 bodov, kategória Z
Raz neskoro večer na matfyze si Zemčo všimol, že už je strašne veľa hodín. Tak sa
pobral domov. Avšak cestou si všimol, že v trinástom akvárku je niečo napísané na tabuli.
Tak sa tam vybral a uvidel tam napísané:
"Práve 4 z týchto výrokov sú pravdivé."
"Práve 3 z týchto výrokov sú pravdivé."
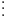
"Práve 47 z týchto výrokov je pravdivých."
A tak začal rozmýšľať a rozmýšľať, koľko že to vlastne výrokov je pravdivých.
Avšak Zemčo musí byť o desiatej doma, preto mu pomôžte, nech to stihne.
Úloha
Prvý riadok vstupu obsahuje počet výrokov 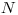
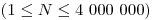 Potom nasleduje
Potom nasleduje 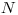 riadkov, každý z nich obsahuje jedno nezáporné
celé číslo
riadkov, každý z nich obsahuje jedno nezáporné
celé číslo 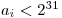 reprezentujúce
výrok "Práve
reprezentujúce
výrok "Práve 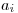 z týchto výrokov je pravdivých.".
z týchto výrokov je pravdivých.".
Na výstup vypíšte práve jeden
riadok obsahujúci počet pravdivých výrokov.
Ak môže byť správnych viac odpovedí, vyberte z nich tú najväčšiu možnú.
Ak neexistuje žiadna správna odpoveď, vypíšte riadok obsahujúci 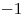 .
.
Pre odovzdanie tejto úlohy je potrebné byť registrovaný na Liahni a odovzdať riešenie na adrese
https://liahen.ksp.sk/task.php?task_id=43
(úloha je medzi špeciálnymi úlohami a volá sa vyroky).
Pri odovzdávaní bude riešenie otestované na príkladoch zo zadania – takto si môžete overiť, či máte správny formát vstupu a výstupu. Po termíne odovzdania riešení bude posledné odovzdané riešenie každého z riešiteľov otestované na iných testovacích vstupoch. Body za túto úlohu dostanete podľa úspešnosti vašich programov pri testovaní. Prosíme vás zároveň, aby ste si po registrácii vyplnili svoje celé meno, aby sme vedeli, komu body patria. Kto tak nespraví, body za túto úlohu nedostane.
Vstup
5 0 0 1 2 3Výstup
1
Vstup
10 1 2 2 3 3 3 4 4 4 4Výstup
4
Vstup
2 0 3Výstup
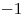
(Ak by sme vypísali 0, tak by to znamenalo, že prvý výrok,
"Práve 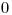 z týchto výrokov je pravdivých.", je pravdivý. Ale
to je v rozpore s ním samým.)
z týchto výrokov je pravdivých.", je pravdivý. Ale
to je v rozpore s ním samým.)
4. Organizácia Kopanie Stôk Prievidza
15 bodov, kategória Z a OV prestížnej organizácii Kopanie Stôk Prievidza (ďalej len KSP) sa chystajú veľké zmeny. Keďže si nikto nevedel zvyknúť na demokraciu a rovnosť všetkých členov, rozhodli sa zaviesť organizačnú štruktúru. Dohodli sa na troch základných bodoch.
- V organizácii bude práve jeden človek, tzv. starý koreň, ktorý nebude mať šéfa.
- Každý okrem starého koreňa musí mať práve jedného šéfa.
- Nikto nemôže byť nadriadeným sám sebe. (Nadriadený = šéf, šéfov šéf, šéf šéfovho šéfa,
atď.)
Všetci dobre vieme, že dôležité sú tie nepísané pravidlá. A keďže chceli predísť hádkam, zaviedli si nasledovné.
- Ak sa nejakí dvaja ľudia často hádajú a nevedia sa dohodnúť, (To by ste neverili,
koľko takýchto dvojíc sa nájde...)
musí jeden z nich v novej štruktúre byť nadriadeným (pozor, nie nutne priamo
šéfom) toho druhého.
No a preto, aby si na seba zvykli aj tí pohádaní ľudia, a čiastočne aj z prirodzenej škodoradosti, vzniklo ešte jedno pravidlo.
- Každý musí byť rozhádaný so všetkými, ktorým bude šéfom.
Úloha
Na prvom riadku vstupu sú zadané celé čísla 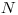 a
a 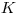 .
Číslo
.
Číslo 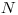 vyjadruje počet všetkých členov organizácie,
vyjadruje počet všetkých členov organizácie, 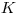 je počet pohádaných dvojíc.
Nasledujúcich
je počet pohádaných dvojíc.
Nasledujúcich 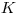 riadkov obsahuje dvojice čísel
riadkov obsahuje dvojice čísel 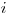 a
a 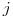
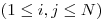 ,
ktoré hovoria o tom, že
,
ktoré hovoria o tom, že 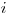 -ty člen je pohádaný s
-ty člen je pohádaný s 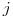 -tym a naopak.
-tym a naopak.
Vašou úlohou je nájsť ľubovoľnú organizačnú štruktúru, ktorá spĺňa všetkých päť vyššie uvedených pravidiel a je v nej každý člen.
Ak taká neexistuje, vypíšte o tom príslušnú správu. Ak existuje, tak pre každého člena vypíšte zoznam členov, ktorým bude šéfovať.
Príklad
Vstup
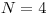 ,
, 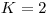 1 2
4 3
1 2
4 3
Výstup
Nie je možné vytvoriť organizačnú štruktúru.Vstup
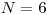 ,
, 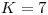 3 4
2 4
3 2
2 5
3 5
5 6
1 5
3 4
2 4
3 2
2 5
3 5
5 6
1 5
Výstup
1: 2: 3 3: 4 4: 5: 1, 2 6: 55. Opály, zafíry, a iné drahé kamene
15 bodov, kategória Z a OMaty prišiel do Klubu Mladých Striebrotepcov a všimol si na stole nádherný náhrdelník zostavený z lesknúcich sa drahých kameňov. Ihneď sa mu zapáčil a dostal chuť taký náhrdelník vlastniť. (Nikdy nemôžete vedieť, kedy sa vám taký náhrdelník zíde.) . Preto začal skúmať, ako je zostrojený, a podarilo sa mu spraviť dve pozorovania: Náhrdelník je zložený z drahých kameňov, ktoré sa lesknú. Kamene sa v náhrdelníku lesknú viac, ako keď sú každý zvlášť, lebo keď sú v náhrdelníku, tak sa svetlo môže odrážať od susedných kameňov.
Presnejšie to funguje takto. Lesk každého kameňa je nejaké kladné celé číslo.
Keď teraz pospájame kamene do náhrdelníka, zvýši sa lesk každého kameňa
o lesk jeho susedov.
(Úplne formálne, lesk 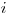 -teho kameňa v náhrdelníku je súčet pôvodných
leskov
-teho kameňa v náhrdelníku je súčet pôvodných
leskov 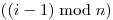 -teho,
-teho, 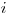 -teho a
-teho a
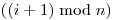 -teho kameňa).
-teho kameňa).
Úloha
Na prvom riadku vstupu je dané kladné celé číslo 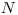 , označujúce počet drahých kameňov, z ktorých je náhrdelník zostavený.
Na druhom riadku je
, označujúce počet drahých kameňov, z ktorých je náhrdelník zostavený.
Na druhom riadku je 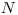 kladných celých čísel
kladných celých čísel 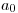 až
až 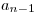 . Tieto čísla udávajú, ako
lesklé sa Matymu zdali jednotlivé kamene náhrdelníka, ktorý videl.
Vašou úlohou je zistiť, aké boli pôvodné lesky kameňov, z ktorých bol
náhrdelník zostrojený.
Ak existuje viac možností, ako mohli vyzerať pôvodné kamene, tak stačí vypísať jednu.
Ak neexistuje žiadna sada kameňov, z ktorých by sa dal zostrojiť daný náhrdelník, vypíšte, že ide o falzifikát.
. Tieto čísla udávajú, ako
lesklé sa Matymu zdali jednotlivé kamene náhrdelníka, ktorý videl.
Vašou úlohou je zistiť, aké boli pôvodné lesky kameňov, z ktorých bol
náhrdelník zostrojený.
Ak existuje viac možností, ako mohli vyzerať pôvodné kamene, tak stačí vypísať jednu.
Ak neexistuje žiadna sada kameňov, z ktorých by sa dal zostrojiť daný náhrdelník, vypíšte, že ide o falzifikát.
Vstup
5
3 3 3 3 3
Výstup
1 1 1 1 1
Vstup
4
7 6 9 8
Výstup
1 2 3 4
6. Obchod
15 bodov, kategória OIstá nemenovaná spoločnosť práve prichádza na trh s novým výrobkom. Analýzou databázy predošlých nákupov zistila, koľko najviac je ktorý potenciálny zákazník ochotný zaplatiť za daný výrobok. Samozrejme, spoločnosť chce na svojom výrobku zarobiť čo najviac. Zaviazala sa ale, že náklady na prepravu výrobkov zákazníkom zaplatí sama. Teraz však nie je vôbec ľahké správne určiť cenu tohto nového výrobku.
Úloha
Na vstupe je číslo 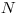 , udávajúce počet potenciálnych zákazníkov a pre každého
zákazníka sú dané dve čísla
, udávajúce počet potenciálnych zákazníkov a pre každého
zákazníka sú dané dve čísla 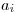 a
a 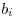 . Číslo
. Číslo 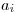 udáva maximálnu cenu,
za ktorú je ochotný
udáva maximálnu cenu,
za ktorú je ochotný 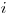 -ty zákazník kúpiť nový výrobok,
-ty zákazník kúpiť nový výrobok, 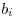 sú prepravné
náklady, ktoré by spoločnosť platila, ak by si tento zákazník výrobok kúpil. Vašou
úlohou je stanoviť cenu (pre všetkých zákazníkov rovnakú), za ktorú sa má nový
výrobok predávať.
sú prepravné
náklady, ktoré by spoločnosť platila, ak by si tento zákazník výrobok kúpil. Vašou
úlohou je stanoviť cenu (pre všetkých zákazníkov rovnakú), za ktorú sa má nový
výrobok predávať.
Pri predaji výrobkov budeme predpokladať dve veci: Spoločnosť ponúkne výrobok práve tým zákazníkom, u ktorých je cena výrobku vyššia ako prepravné náklady. A keďže tento výrobok je taký úžasný, kúpi si ho každý z nich, kto si ho môže za danú cenu dovoliť.
Presnejšie, ak spoločnosť predáva výrobok za cenu 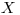 , tak
, tak 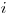 -ty zákazník si
kúpi výrobok práve vtedy, keď
-ty zákazník si
kúpi výrobok práve vtedy, keď 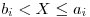 . Zisk spoločnosti z tohto predaja
bude
. Zisk spoločnosti z tohto predaja
bude 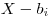 .
.
Ak je riešení (teda možných cien výrobku 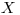 , ktoré maximalizujú zisk)
viac, vypíšte najmenšie nezáporné.
, ktoré maximalizujú zisk)
viac, vypíšte najmenšie nezáporné.
Príklad
Vstup
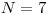 10 2
10 8
20 11
20 15
5 0
17 20
9 3
10 2
10 8
20 11
20 15
5 0
17 20
9 3
Výstup
9 (Za túto cenu si výrobok kúpi prvý, druhý a siedmy zákazník,dostaneme zisk 14. Rovnaký zisk by sme dostali aj pri cene výrobku 20.)
7. Ondrejova hra
15 bodov, kategória O
Ondrej je matfyzák a je to na ňom vidieť. Často máva úplne skvelé nápady, ktoré
ale jeho nematfyzácki kamaráti nevedia pochopiť. Napríklad minule cestoval
vlakom, nudil sa, tak hovorí svojmu prísediacemu: "Tomino, poďme sa zahrať
dáku hru, aby nám čas rýchlejšie ubehol." "To myslíš také tie tvoje hry ako: faktorizuj
polynóm nad 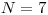 do piatich sekúnd?"
odpovedal Tomáš neprívetivým hlasom, vyberajúc
skriptá z účtovníctva. "Nie, táto je naozaj zaujímavá – prisahám", snažil sa ho Ondrej
presvedčiť. "Počkaj, to si predsa hovoril aj o hentej jednej... Ako to bolo... Aha, už
viem: Ofarbi graf najmenším počtom farieb", odpovedal Tomáš hľadajúc kapitolu
o dlhodobom hmotnom majetku. Ondrej je človek neodbytný a skúša ešte raz: "No tak, Tomino,
však aspoň vyskúšaj, som si istý, že táto hra ťa bude určite baviť." Tomáš je
predsa len v kútiku duše citlivý človek, ktorý nechce Ondreja zarmútiť a nakoniec
sa necháva presvedčiť. Keďže ale už dopredu vie, že Ondrejovej hre bude ledva rozumieť,
žiada vás o pomoc.
do piatich sekúnd?"
odpovedal Tomáš neprívetivým hlasom, vyberajúc
skriptá z účtovníctva. "Nie, táto je naozaj zaujímavá – prisahám", snažil sa ho Ondrej
presvedčiť. "Počkaj, to si predsa hovoril aj o hentej jednej... Ako to bolo... Aha, už
viem: Ofarbi graf najmenším počtom farieb", odpovedal Tomáš hľadajúc kapitolu
o dlhodobom hmotnom majetku. Ondrej je človek neodbytný a skúša ešte raz: "No tak, Tomino,
však aspoň vyskúšaj, som si istý, že táto hra ťa bude určite baviť." Tomáš je
predsa len v kútiku duše citlivý človek, ktorý nechce Ondreja zarmútiť a nakoniec
sa necháva presvedčiť. Keďže ale už dopredu vie, že Ondrejovej hre bude ledva rozumieť,
žiada vás o pomoc.
Úloha
Ondrejova hra je nasledovná: Ondrej si vymyslí 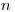 -uholník so stranami rovnobežnými
so súradnicovými osami. Potom nakreslí na štvorčekový papier všetky vrcholy
-uholník so stranami rovnobežnými
so súradnicovými osami. Potom nakreslí na štvorčekový papier všetky vrcholy 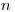 -uholníka,
teda tie body, kde sa stretajú dve po sebe idúce strany (pod uhlom 90 stupňov). Takto pokreslený
papier podá Tomášovi a žiada ho, aby z daných bodov dokreslil celý pôvodný
-uholníka,
teda tie body, kde sa stretajú dve po sebe idúce strany (pod uhlom 90 stupňov). Takto pokreslený
papier podá Tomášovi a žiada ho, aby z daných bodov dokreslil celý pôvodný 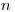 -uholník,
a navyše ešte zistil jeho obsah.
-uholník,
a navyše ešte zistil jeho obsah.
Pre dané 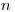 a
a 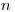 rôznych bodov v rovine nájdite Ondrejov
rôznych bodov v rovine nájdite Ondrejov 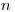 -uholník, ktorého vrcholy
sú práve dané body. Taktiež nájdite obsah tohto
-uholník, ktorého vrcholy
sú práve dané body. Taktiež nájdite obsah tohto 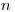 -uholníka.
-uholníka.
Nájdený 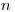 -uholník nesmie nikde sám seba pretínať, ani sa sám seba dotýkať. Inými
slovami, dve strany môžu mať spoločný bod vtedy a len vtedy, ak nasledujú bezprostredne
po sebe na obvode
-uholník nesmie nikde sám seba pretínať, ani sa sám seba dotýkať. Inými
slovami, dve strany môžu mať spoločný bod vtedy a len vtedy, ak nasledujú bezprostredne
po sebe na obvode 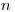 -uholníka.
-uholníka.
Ak pre dané body existuje viac prípustných 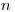 -uholníkov, vyberte si ľubovoľný z nich.
Môžete predpokladať, že vstup je korektný a aspoň jeden prípustný
-uholníkov, vyberte si ľubovoľný z nich.
Môžete predpokladať, že vstup je korektný a aspoň jeden prípustný 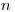 -uholník existuje.
-uholník existuje.
Vstup
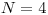
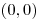 ,
, 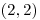 ,
, 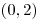 ,
, 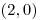
Výstup
Ondrejov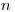 -uholník má body v tomto poradí:
-uholník má body v tomto poradí:
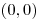 ,
, 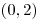 ,
, 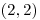 ,
, 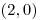 . Obsah je
. Obsah je 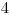 .
.
Vstup
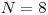
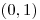 ,
, 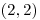 ,
, 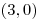 ,
, 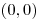 ,
,
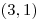 ,
, 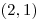 ,
, 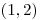 ,
, 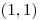
Výstup
Ondrejov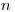 -uholník má body v tomto poradí:
-uholník má body v tomto poradí:
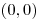 ,
, 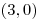 ,
, 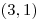 ,
, 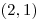 ,
,
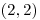 ,
, 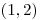 ,
, 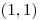 ,
, 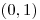 .
Obsah je
.
Obsah je 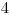 .
.
8. O televíznej hre
15 bodov, kategória O a TPeňazí nikdy nie je dosť a aj KSP sa dlhodobo obzerá po možných zdrojoch príjmu. Keďže je v poslednej dobe v rôznych televíziach toľko zábavných hier a súťaží, rozhodol sa náš seminár, že do jednej z nich pošle svojho zástupcu, ktorý vyhrá majland. Ten sa potom použije na ušľachtilé účely, ako napríklad čiastočné hradenie účastníckeho poplatku na sústredení alebo kvalitnejšie občerstvenie na kapustnici KSP...
I tak sa ocitol Mic v súťažnej hre "Slovensko hľadá hyperlamu", kde musí robiť množstvo hlúpostí. V prvom kole musel zaspievať pesničku, v druhom musel s čo najväčším potešením zjesť Vifon a v treťom vykopať čo najhlbšiu jamu. Keďže vo všetkých týchto aktivitách je doma, nemal problém povyhrávať nad súpermi a dostať sa do finálového kola. V ňom proti nemu stojí posledný súper – Maroško, ktorého poznáte z predchádzajúcich sérii. Micovou úlohou je poraziť ho v poslednej disciplíne: logickej hre.
Princíp disciplíny je nasledovný: do kruhu je rozostavených 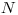 kufríkov s peniazmi.
kufríkov s peniazmi.
V každom je nejaká suma (vždy samozrejme kladná). Obaja súťažiaci tieto sumy poznajú. Súperi sa striedajú v ťahaní, pričom Mic začína. Vyberie si jeden kufrík a ten si privlastní. Nasleduje Maroško, ktorý spraví to isté spomedzi tých kufríkov, ktoré ostali. Teraz z pôvodného kruhového rozostavenia ostal jeden alebo dva súvislé úseky. Hra pokračuje nasledovne: hráč, ktorý je na ťahu, si vyberie práve jeden kufrík z každého súvislého úseku, ktorý ostal. Týmto ťahom ho prípadne môže rozdeliť na dva kratšie. Hra končí, keď už neostanú žiadne kufríky.
Maroško je poriadne motivovaný, pretože by rád vyhral peniaze na novú pohovku. Aj nám všetkým však na výsledku veľmi záleží. A aj vám by malo – čím viac totiž Mic vyhrá, tým lacnejšie budete mať sústredenie. (Ak sa všetko neminie na spomínanej kapustnici...)
Úloha
Pre dané číslo 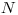 a
a 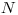 súm v kufríkoch vypočítajte, koľko najviac môže Mic nahrať za
predpokladov, že Maroško bude ťahať optimálne a Mic začína.
súm v kufríkoch vypočítajte, koľko najviac môže Mic nahrať za
predpokladov, že Maroško bude ťahať optimálne a Mic začína.
Vstup
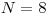
2 1 4 1 2 1 8 1
Výstup
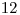 (Mic v prvom ťahu zoberie 8. Ak by Maroško nechal Micovi 4, Mic by určite nahral viac
ako 12. Preto Maroško vezme 4. Tým zostanú dva rovnaké úseky "1 2 1". Z každého Mic vezme 2,
a Maroško poberie všetok zvyšok.)
(Mic v prvom ťahu zoberie 8. Ak by Maroško nechal Micovi 4, Mic by určite nahral viac
ako 12. Preto Maroško vezme 4. Tým zostanú dva rovnaké úseky "1 2 1". Z každého Mic vezme 2,
a Maroško poberie všetok zvyšok.)
Vstup
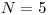
10 5 6 5 9
Výstup
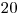
9. Tóny ľubozvučných melódií
15 bodov, kategória TKSPákov posadla UltrastarMánia. Prejavuje sa to hlasným spevom na chodbách, prednáškach, ale aj na uliciach. Aj keď ťažko povedať, či sa to dá vždy nazvať spevom. Ako k tomu prišlo? Raz dávno niekoho napadlo, že videl KSPákov robiť už všeličo, ale ešte ich nepočul spievať. Táto krvilačná myšlienka sa podarila uskutočniť. Jeden slnečný deň si vojde KSPák do T2 a zrazu... Nemôže ani dnu, ani von, musí odspievať pesničku. Dajú mu slúchadlá, mikrofón a skladba beží... Na monitore poskakujú noty a text, chudák nemá iné východisko. Ale celkom mu to ide. Každú desiatu notu trafil.
Časom sa medzi KSPákmi vyvinula chorobná súťaživosť. Niektorým na výsledku začalo tak záležať, že rozmýšľali nad rôznymi spôsobmi, ako maximalizovať svoj výkon. A tak niekto dostal nápad, že keď budú spievať viacerí naraz, majú väčšiu šancu trafiť sa, a teda môžu urobiť rekord. Ba čo rekord! Všetky noty v pesničke chcú trafiť!
Úloha
Na vstupe je celé číslo 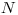 , ktoré vyjadruje počet tónov v pesničke. Potom
nasleduje
, ktoré vyjadruje počet tónov v pesničke. Potom
nasleduje 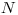 riadkov, každý obsahuje tri kladné celé čísla: čas štartu, dĺžku tónu
(obe v rovnakých časových jednotkách) a výšku tónu, ktorý vtedy treba spievať.
riadkov, každý obsahuje tri kladné celé čísla: čas štartu, dĺžku tónu
(obe v rovnakých časových jednotkách) a výšku tónu, ktorý vtedy treba spievať.
Už pôvodná pieseň mohla byť robená pre viachlas, preto v jednom časovom úseku môže byť naraz potrebné spievať aj viacero tónov. KSPáci nie sú nejakí extra dobrí v speve. Jediné, čo taký KSPák vie, je, že vždy po uplynutí časovej jednotky môže (ak chce) okamžite zvýšiť alebo znížiť spievaný tón o jedna. Začať spievať môže na hociktorej výške tónu.
Vašou úlohou je vypočítať minimálny počet spevákov, ktorí spolu dokážu presne odspievať celú pesničku,
Príklad
Vstup
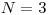 1 2 3
4 3 4
3 1 2
1 2 3
4 3 4
3 1 2
Výstup
2 (Napr.: Prvý spevák začne spievať v čase 1 tón 3, v čase 3 ho zmení na 2, v čase 4 na 3 a v čase 5 na 4.Tým ostal pre druhého speváka v čase 4 až 5 nezaspievaný tón výšky 4.)
10. – je v morzeovke T
15 bodov, kategória TRádioamatéri sú fakt veľkí makači. Vedia napríklad vysielať v morzeovke. A to výrazne rýchlejšie, ako napríklad vy, keď píšete SMSky. Kto nevie naspamäť morzeovku, nájde ju na http://en.wikipedia.org/wiki/Morse_code
Jeden sobotný večer počúval Móricko svojho otca, ako vysiela. Pri rýchlosti okolo 40 odvysielaných slov za minútu však Móricko nemal ani najmenšiu šancu vysielaniu porozumieť. Stihol si akurát tak zapisovať bodky a čiarky s tým, že neskôr si to predsa v pokoji dekóduje.
Zabudol ale na dôležitú vec -- zapísať si aj oddeľovače, ktoré hovoria, kde kód jedného znaku končí a druhého začína. A teraz má problémy: je –.–. C, KE, či nebodaj TETE?
Móricko je ale veľký pán programátor, a tak sa rozhodol, že použije slovník. Zapísaný reťazec bodiek a čiarok naseká na kusy tak, aby každý kus bol kódom nejakého slova zo slovníka. Lenže ešte netuší, že ani tento trik mu nemusí stačiť.
Úloha
Máme N <= 10000 slov tvoriacich slovník a reťazec bodiek a čiarok dĺžky L <= 10000. Slová v slovníku majú dĺžky do D = 20. Napíšte program, ktorý vypočíta, koľko rôznych postupností slov zo slovníka dá po zakódovaní do morzeovky zadaný reťazec.
Poznámky
Stačí, aby program fungoval pre vstupy, kde sa výstup zmestí do bežnej celočíselnej premennej. Za riešenie s časovou zložitosťou θ(LND) veľa bodov nečakajte, a za pomalšie už vôbec nie.

