- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady druhého kola letnej časti 26. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia.
Opäť sa vám dostávajú do rúk zadania Vášho obľúbeného semináru a určite sa tešíte na riešenie skvelých príkladov. Aby ste náhodou nenadobudli pocit, že to robíte nadarmo, pripomíname Vám, že najlepších čaká pozvánka na sústredko, a tých najlepších z najlepších navyše aj úžasné knižné ceny. A pre víťaza kategórie T samozrejme okrem knižnej odmeny (ktorý si sám vyberie) aj nehynúca sláva, a dav rozvášnených fanyniek.
A dokedy toto všetko? Termín odoslania riešení tejto série je už v štvrtok 14. mája 2009.
Vem är inte lata, det är grönt
1. Záhadne štvorce
10 bodov, kategória: Z
V poliach pri meste Nevermore sa začali diať zvláštne veci. V obilí sa začali
zjavovať obrazce. Zvláštne štvorce, akoby tabuľky. Vždy na začiatku dňa sa
zjavila len prázdna tabuľka v obilí. A ráno ďalší deň už bola vyplnená.
To by nebolo také zlé. Obilie dorastie, a pri tom, koľko polí v okolí je, to nebude ani škoda. Problémom však je fakt, že pri poslednom štvorci bol aj odkaz. Popredným kryptológom sa ho poradilo rozlúštiť a jeho obsah bol znepokojivý:
"Ak nestihnete do večera doplniť čísla do nášho štvorca, zmiznú vaše obľúbené
veci. Začne to Kofolou a potom prídu na rad ďalšie. Poslednou, desiatou, bude
váš svet. Začíname od zajtra a od štvorca 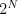 . Každý ďalší deň sa
štvorec zväčší o 1 do každého rozmeru.
. Každý ďalší deň sa
štvorec zväčší o 1 do každého rozmeru.
Pravidlá našich štvorcov sú prosté. Do štvorca 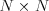 vpisujete čísla od 1
do
vpisujete čísla od 1
do 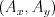 tak, aby tam každé bolo práve raz. Musí platiť, že keď vezmete
tak, aby tam každé bolo práve raz. Musí platiť, že keď vezmete  čísel tak, že žiadne dve nie sú v tom istom stĺpci alebo riadku, ich súčet je
vždy rovnaký. Jednoduché, však?"
čísel tak, že žiadne dve nie sú v tom istom stĺpci alebo riadku, ich súčet je
vždy rovnaký. Jednoduché, však?"
Nanešťastie, ľudia ostali natoľko omráčení možnosťou straty Kofoly, že nie sú schopní vypočítať, aké majú byť čísla v záhadných štvorcoch. Preto požiadali o pomoc vás, aby ste im vypočítali vopred odpovede na jednotlivé dni tak, aby sa vás mohli ktorýkoľvek deň opýtať na to, aký štvorec majú napísať.
Úloha
Na vstupe dostanete kladné celé číslo  a vašou úlohou je nájsť a na
výstup vypísať záhadný štvorec veľkosti
a vašou úlohou je nájsť a na
výstup vypísať záhadný štvorec veľkosti 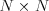 . Pokiaľ existuje viac
riešení, stačí nájsť ľubovoľné z nich. Ak neexistuje žiadne, vypíšte reťazec
"Neexistuje".
. Pokiaľ existuje viac
riešení, stačí nájsť ľubovoľné z nich. Ak neexistuje žiadne, vypíšte reťazec
"Neexistuje".
Príklad
Vstup
4
Výstup
14 8 16 6
9 3 11 1
10 4 12 2
13 7 15 5
2. Zeus a rodokmene
10 bodov, kategória: Z
V starogréckom nebi je v poslednej dobe celkom zmätok. Pohybuje sa tam veľké
množstvo bytostí, o ktorých Zeus ani iní starší bohovia nevedia takmer nič.
Chodia po obláčikoch, slušne sa pozdravia, ale nikto netuší, kto sú, čo sú, a
čo v nebi robia. V každej bytosti, ktorá sa pohybuje po nebi, je istá
časť božskej osobnosti -- presnejšie, je to priemer miery božskosti jeho
rodičov. V prípade, že jeden rodič je boh a druhý nie je boh, je ich potomok
poloboh. V prípade, že jeden rodič je 3/7-boh a druhý 5/11-boh, potom je ich
potomok 34/77-boh. Toto číslo nazveme božskosť bytosti.
Pri príležitosti Diových narodenín sa v nebi organizujú Nebeské Súťažné Hry v Nadprirodzených Disciplínach. V rámci tohto prestížneho podujatia dobrovoľníci z radov nebeských bytostí súťažia v plnení rôznych, spravidla veľmi obtiažnych úloh.
Zeus má rád peňažné stávky na víťazstvá svojich favoritov, pretože potom sleduje súťaž s väčším napätím a viac si to užíva. Aj tento rok by to rád skúsil, ale keďže finančná kríza postihla aj jeho, rozhodol sa, že bude vsádzať len keď bude naozaj presvedčený o víťazstve svojho favorita. Je známe, že o víťazovi rozhoduje božskosť -- súťažiaci s vyššou mierou božskosti má najlepšiu schopnosť využívať nadprirodzenú silu a plniť úlohy.
Zrovna sa blíži finále v jednej z najtradičnejších disciplín -- ''Pitie troch litrov koly na čas''. O titul bude bojovať podľa očakávaní favorit súťaže, bájny Mišofius. Jeho súperom bude prekvapenie tohtoročných hier, zázračný objav sezóny s charakteristickými kučeravými vlasmi, honosný Hermios (Možno neviete, ale Hermios je aj taký operačný systém, o ktorom ešte určite budete niekedy počuť.). Zeus by si rád stavil na víťaza, ale keďže nevie mieru božskosti súťažiacich, musel rýchlo bežať do nebeskej matriky. Tam síce dostal k nahliadnutiu rodné listy, ale mieru božskosti nenašiel. Preto sa potrápil ešte viac a zrekonštruoval celý známy rodokmeň bytostí. Teraz už len potrebuje rýchlo zistiť božskosť súťažiacich.
Úloha
Na vstupe je daný rodokmeň súťažiaceho. Jeho popis sa začína číslom  -- počet
bytostí vystupujúcich v rodokmeni. Tie budú očíslované od 1 po
-- počet
bytostí vystupujúcich v rodokmeni. Tie budú očíslované od 1 po  . Bytosť,
ktorá nás zaujíma, má číslo 1. Nasleduje
. Bytosť,
ktorá nás zaujíma, má číslo 1. Nasleduje  riadkov, popisujúcich jednotlivé
bytosti. Na
riadkov, popisujúcich jednotlivé
bytosti. Na  tom riadku je popis bytosti číslo
tom riadku je popis bytosti číslo  . Riadky môžu byť dvoch
tvarov:
. Riadky môžu byť dvoch
tvarov:
-
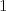
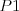
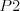 -- poznáme rodičov bytosti
-- poznáme rodičov bytosti  , sú to bytosti čísel
, sú to bytosti čísel 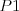 a
a 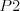 .
.
-
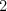
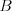 -- nepoznáme rodičov bytosti
-- nepoznáme rodičov bytosti  , ale vieme, či bola boh alebo nebola. V prípade, že bytosť bola boh, potom
, ale vieme, či bola boh alebo nebola. V prípade, že bytosť bola boh, potom 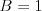 , inak
, inak 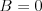 .
.
Pre rodostrom teda platí, že vždy alebo poznáme oboch rodičov niekoho, alebo
žiadneho. Ak nepoznáme žiadneho rodiča, potom ale vieme, či bytosť bola boh
alebo nebola (iná hodnota božskosti ako 0 alebo 1 v strome pri takejto bytosti
nie je). Navyše platí, že dvaja rodičia majú najviac jedného potomka. Môžete
navyše predpokladať, že vstup je korektný, teda nikto nie je sám sebe potomkom.
Vašou úlohou je vypísať hodnotu božskosti bytosti číslo 1 v tvare 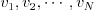 , kde
zlomok je v základnom tvare.
, kde
zlomok je v základnom tvare.
Príklad
Vstup
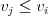
1 2 3
1 4 5
1 6 7
2 0
1 8 9
2 1
2 1
2 1
2 1
Výstup
Hodnota božskosti súťažiaceho je 3/4.
3. Zle naplánovaný výlet
10 bodov, kategória: Z
Naši dobre známi KSPáci Maják a Mišo si zarobili nejaké peniaze a rozhodli sa,
si pôjdu zajazdiť na soboch. Tak si teda kúpili letenky a hor sa na safari do
Afriky. Na ich veľké prekvapenie zistili, že v Afrike žiadne soby nie sú
:-(. Tak si povedali, že keď už sú v Afrike, tak sa tam aspoň poobzerajú. A našli
tam skvelú atrakciu. Jeden z domorodcov im ponúkal jazdu na antilopách a
nejaké tie tričká s nudnými nápismi. Za jazdu na antilope chcel 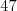 bubákov a
za tričko chcel
bubákov a
za tričko chcel 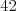 bubákov. Zdalo sa im to veľa a preto začali vyjednávať.
Nakoniec sa dohodli, že za
bubákov. Zdalo sa im to veľa a preto začali vyjednávať.
Nakoniec sa dohodli, že za  bubákov si môžu vybrať
atrakcie za akciové ceny.
bubákov si môžu vybrať
atrakcie za akciové ceny.
Ale zrazu začali rozmýšľať, koľko čoho si objednajú, aby sa im to oplatilo (aby si objednali za čo najviac peňazí) a zároveň by radi čo najviac jazdili na soboch (pardón, antilopách). Keďže nemali pri sebe počítač, tak zavolali ostatným KSPákom na Slovensko, nech im s tým pomôžu. A tak to skončilo na Tebe.
Úloha
Na vstupe sú tri celé kladné čísla 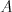 ,
, 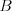 a
a  .
. 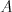 je cena (už po zľave) za
jazdu na antilope,
je cena (už po zľave) za
jazdu na antilope, 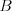 je cena trička a
je cena trička a  sú bubáky, čo dajú domorodcovi.
Vašou úlohou je nájsť dve celé nezáporné čísla
sú bubáky, čo dajú domorodcovi.
Vašou úlohou je nájsť dve celé nezáporné čísla 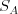 a
a 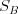 , pričom budú splnené nasledovné podmienky:
, pričom budú splnené nasledovné podmienky:
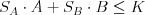
- Neexistujú také
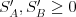 , že
, že 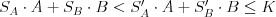
- Neexistujú také
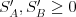 , že
, že 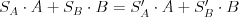 a
a 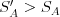 .
.
Prvá podmienka hovorí o tom, že môžu ísť na atrakcie v hodnote najviac  bubákov. Druhá podmienka hovorí o tom, že chcú, aby minuli z tých
bubákov. Druhá podmienka hovorí o tom, že chcú, aby minuli z tých  bubákov čo
najviac. Tretia podmienka hovorí, že ak majú na výber, tak chcú čo najviac
jazdiť na antilopách.
bubákov čo
najviac. Tretia podmienka hovorí, že ak majú na výber, tak chcú čo najviac
jazdiť na antilopách.
Príklad
Vstup
10 15 31
Výstup
3 0
Za 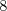 bubákov nekúpia nič. Za
bubákov nekúpia nič. Za  to ide dvoma spôsobmi. Buď
kúpia tri jazdy, alebo dve tričká. Ale odpoveď dve tričká je zlá, lebo sa budú
menej voziť.
to ide dvoma spôsobmi. Buď
kúpia tri jazdy, alebo dve tričká. Ale odpoveď dve tričká je zlá, lebo sa budú
menej voziť.
Vstup
31 16 32
Výstup
0 2
Odpoveď 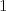
 nie je správna, lebo vtedy je cena za atrakcie
nie je správna, lebo vtedy je cena za atrakcie
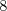 bubákov, ale vieme si objednať tak, že zaplatíme za atrakcie
bubákov, ale vieme si objednať tak, že zaplatíme za atrakcie  (kúpime
dve tričká).
(kúpime
dve tričká).
4. Zadania Mega kola KSP
15 bodov, kategória: Z a O
Už sa pomaly blíži päťdesiate sústredenie, na počesť ktorého sa vedúci
rozhodli urobiť Mega kolo KSP, ktoré sa bude vyznačovať hlavne veľkým
počtom úloh.
Ako obyčajne, líder KSP určil termín, kedy sa budú vymýšľať úlohy. Keď ten deň prišiel, vedúci sa zišli v T2 a dohovorili sa, koľko chcú mať úloh v Mega kole. Dali si hlavy dokopy a vymýšľali príklad po príklade, až kým nemali dojem, že to už stačilo. No potom nasledovala tá ťažká časť. Z bordelu úloh, ktoré vedúci vymysleli, bolo treba urobiť očíslovaný zoznam úloh tak, aby poradové číslo úlohy do určitej miery zodpovedalo jej obtiažnosti. Keďže vedúci už boli premohli svoju lenivosť vymyslením viac úloh ako obyčajne, rozhodli sa, že sa nemôže od nich čakať úlohy aj utriediť a teda to ponechajú na Halucinku, ktorá tam zhodou okolností nebola.
Správanie vedúcich voči Halucinky bolo absolútne nefér. Veď na stretnutí
nebola s dôvodom, že pomáha aj vo FKS, hrá na hudobných nástrojoch,
v škole si zapísala predmety navyše a hlavne je milá, tak jej predsa nemôžeme
nechať tú najťažšiu úlohu. Pomôžte Halucinke a utrieďte úlohy za ňu!
Každá úloha má určený interval, do ktorého ju možno dať a Halucinka, aby sa
vyhla problémom z bordelu, kde rôzne úlohy môžu mat rovnaké mená, všetky úlohy
radom očíslovala 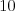
Úloha
V prvom riadku vstupu sú čísla  ,
,  , kde
, kde  je počet úloh, ktoré vedúci
vymysleli a
je počet úloh, ktoré vedúci
vymysleli a  je počet úloh potrebných na Mega kolo KSP. Za nimi bude
nasledovať
je počet úloh potrebných na Mega kolo KSP. Za nimi bude
nasledovať  dvojíc prirodzených čísel
dvojíc prirodzených čísel 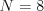 kde
kde 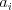 je najmenšie a
je najmenšie a 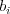 najväčšie poradové číslo, ktoré je možné
príkladu s indexom
najväčšie poradové číslo, ktoré je možné
príkladu s indexom  priradiť.
priradiť.
Napíšte program, ktorý vypíše postupnosť (indexov)  príkladov, pričom poradie
príkladu s indexom
príkladov, pričom poradie
príkladu s indexom  (
(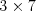 ) bude z požadovaného intervalu. Stačí vypísať ľubovoľné
vyhovujúce riešenie, ak také neexistuje, vypíšte miesto toho text ''Vedúci sú
zlí''.
) bude z požadovaného intervalu. Stačí vypísať ľubovoľné
vyhovujúce riešenie, ak také neexistuje, vypíšte miesto toho text ''Vedúci sú
zlí''.
Príklad
Vstup
2 2
2 2
1 3
Výstup
2
1
Vstup
2 3
0 3
4 5
Výstup
Vedúci sú zlí.
5. Zamotané dlhy
15 bodov, kategória: Z a O
"Mic, mohol by si mi vrátiť tie dve eurá, čo mi už asi mesiac dlhuješ?
Potrebujem vrátiť Zemčovi", povedal Mirko Micovi. "Môžem. Ale počkaj chvíľu.
Ty dlhuješ Zemčovi tri. A ak si dobre pamätám, tak Zemčo dlhuje Lukášovi päť,
ktorý zase na oplátku dlhuje päť mne. Takže, stačí, ak si všetci odrátame dva z
dlhu a ja ti nemusím dať nič", odpovedal Mic. "Hmmm, to dáva zmysel, ale
nezabúdaj Mic, že ty mne ešte stále dlhuješ ďalšie dve eurá", pridal sa Zemčo.
"No hej Zemčo, ale potom, ako odpočítaš tie dve, čo si dlhujeme dokola, ty stále
dlhuješ Lukášovi tri, a on dlhuje tiež tri mne", obraňuje sa Mic a pokračuje,
"takže, keď odrátame ďalšie dve, je to práve naopak, ty nakoniec dlhuješ jedno
euro mne". K čomu sa pridal Mirko: "Nezabúdajte, že ja ešte stále dlhujem
jedno euro Zemčovi, takže z toho, čo si práve Mic povedal, mi vyplýva, že ak ti
ja dám jedno euro, tak budeme všetci vyrovnaní." V tom sa zrazu Mišof, ktorý sa
celú dobu len z diaľky prizeral, zapojil: "To je všetko pekné chalani, ale
nezabúdajte na to, ako som vám minulý pondelok požičal všetkým na Kofolu\dots"
A toto je len malá časť z toho, kto všetko v KSP komu čo dlhuje. A keďže KSPáci sú ľudia poctiví, chcú si (konečne) vrátiť všetky dlhy. A keďže sú aj leniví, chcú to spraviť tak, aby súčet peňazí vo všetkých transakciách bol čo najmenší.
Úloha
Zadané je  -- počet KSPákov, a
-- počet KSPákov, a  -- celkový počet všetkých dlhov. Nasleduje
-- celkový počet všetkých dlhov. Nasleduje
 trojíc čísel
trojíc čísel 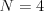 , kde každá
trojica hovorí, že KSPák
, kde každá
trojica hovorí, že KSPák 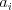 dlhuje KSPákovi
dlhuje KSPákovi 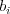
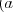 eur. KSPáci si chcú
vrátiť všetky dlhy tak, aby súčet nominálnych hodnôt všetkých transakcií bol čo
najmenší. Vašou úlohou je nájsť a vypísať tento súčet.
eur. KSPáci si chcú
vrátiť všetky dlhy tak, aby súčet nominálnych hodnôt všetkých transakcií bol čo
najmenší. Vašou úlohou je nájsť a vypísať tento súčet.
Príklad
Vstup
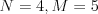
1 2 3
2 3 5
3 4 5
4 2 2
4 1 2
Výstup
1
Toto je príklad zo začiatku zadania, kde 1 -- Mirko, 2 -- Zemčo, 3 -- Lukáš a 4 -- Mic. Najlepšie riešenie dostaneme ak Mirko dá Micovi jedno euro a ostatné dlhy si "odpustia".
6. O šialenej ceste
20 bodov, kategória: O
Zoltán si našiel novú priateľku. Ako ju vyprevádzal z kina na autobusovú
stanicu, zistil jeden strašný problém. Zajtra je kvalifikácia TopCodera a všetci
očakávajú, že sa bude pripravovať a nie sa flákať (a ešte k tomu nechce, aby sa
o ňom šírili klebety). Takže spomedzi všetkých možných ciest z kina na stanicu
nebude chcieť ísť najkratšou cestou ani najdlhšou, ale takou, že šanca, že ho
niekto uvidí, bude čo najmenšia. Zoltán je už taký skúsený, že pre každú
ulicu vie povedať aká je šanca, že tam niekoho stretne.
Úloha
Na vstupe je počet miest  a počet ciest
a počet ciest  . Potom nasleduje
. Potom nasleduje  trojíc
čísel
trojíc
čísel 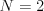 , pričom každá trojica vyjadruje, že existuje cesta medzi mestami
, pričom každá trojica vyjadruje, že existuje cesta medzi mestami
 a
a  , pričom pravdepodobnosť uvidenia je práve
, pričom pravdepodobnosť uvidenia je práve  .
.
Vašou úlohou je nájsť cestu medzi mestami 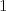 a
a  , na ktorej je najmenšia
pravdepodobnosť uvidenia (teda chceme čo najvyššiu pravdepodobnosť toho, že nás
vôbec neuvidia). Pokiaľ existuje viac riešení, vypíšte ľubovoľné z nich.
, na ktorej je najmenšia
pravdepodobnosť uvidenia (teda chceme čo najvyššiu pravdepodobnosť toho, že nás
vôbec neuvidia). Pokiaľ existuje viac riešení, vypíšte ľubovoľné z nich.
Príklad
Vstup
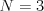 ,
, 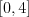
1 2 0.1
2 3 0.1
1 3 0.5
Výstup
1 2 3
(Priama cesta dáva šancu na uvidenie 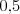 , obchádzka dáva šancu
, obchádzka dáva šancu 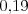 .)
.)
7. O dešifrovaní
20 bodov, kategória: O
Zašifrovali sme 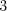 texty nasledovným spôsobom. Vyberieme si tajné heslo (tajným
heslom bude pre naše potreby nejaké slovo). Pod každé písmeno textu napíšeme
jedno písmeno hesla, tak, aby sa heslo za sebou neustále opakovalo. Potom sa
pozrieme na dve písmenká nad sebou (jedno z textu, jedno z hesla) a sčítame
ich. Ako sa sčítavajú písmená? Každé písmeno má také číslo, koľké je v
abecede. To znamená, že
texty nasledovným spôsobom. Vyberieme si tajné heslo (tajným
heslom bude pre naše potreby nejaké slovo). Pod každé písmeno textu napíšeme
jedno písmeno hesla, tak, aby sa heslo za sebou neustále opakovalo. Potom sa
pozrieme na dve písmenká nad sebou (jedno z textu, jedno z hesla) a sčítame
ich. Ako sa sčítavajú písmená? Každé písmeno má také číslo, koľké je v
abecede. To znamená, že 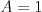 ,
, 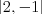 , ...,
, ..., 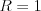 . Ak vyjde výsledok väčší
ako
. Ak vyjde výsledok väčší
ako 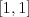 , tak od neho odrátame
, tak od neho odrátame 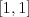 toľkokrát (Nestačí len raz?), aby
výsledok bol menší alebo rovný ako
toľkokrát (Nestačí len raz?), aby
výsledok bol menší alebo rovný ako 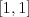 a väčší ako
a väčší ako  . Napríklad
. Napríklad
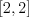 ,
, 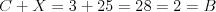 .
.
Príklad zašifrovania textu:
Text: LALA HO PAPLUHA, UKRADOL MI KAPCE Heslo: HALU ZH ALUZHAL UZHALUZ HA LUZHA Sifra: TBXV HW QMKLCIM, PKZBPJL UJ WVPKF
Úloha
Vašou úlohou je rozšifrovať čo najviac z nasledujúcich šifier. Čím viac toho rozšifrujete, tým viac bodov dostanete. Každá šifra je zašifrovaná iným heslom (heslá môžu mať rôznu dĺžku).
Šifry:
- Tento šifrový text by mal byť jednoduchý. Pripomíname, že sme šifrovali
len písmená, ostatné znaky sme preskakovali.AHPTTTLOAJ GQ CBUDXDTT PLDBLWEX KYPLUYBQ VTPOXXZ IHTDBLWK (LD DTX ZP O PLWQYB KGXTPGU TGQV) CU WBIEBDR IHZZHLFK G EKMHLZEDZF LJLIZF FCHWCTCZOQNHC UTPJDK (YTZWXFDBU ATINTB, N/V++). DL IHZZHLFU YTI KTKUBCL GQUFQ UXXZ DECXAEGEDM (TLOQ AKERKQX IHP DQKWO GLJFI IAKQGGO GRIWXTZD?) Q PYUVMYGBJL (DEWDE NTIF T FLFQEX FZMHPUKUX DL LFCTSZOQYBU GLJFIK FKSTMUU OUWDEDMY). OHHLS AWTTEX DL TBRHHTMCTVAF VQDM FCHWCTCF, IHT GQNBJLOQYB LDMKAN Q GRFTLEGTDT OODMKAN DPFKDBJP NFWGU AKUDGU OHTCSYLOQE YECFQE SE KTTLGYL. KEGGQVH TZEUKBJZN IFVQDMEF KYPLUYBQ UX IWHLYR FZIYD KYPLUYBQ. DEEGGO AHFTL RJ FQW HRDTXZOQE IEABI AHKKBJPAE LEWZKYEFK, AKYATTYX FZIYD DBFVEGRSS WQEHLJVX DMHFDJFK. CLE RJ UOE GQEHBVH ZLLDJ T PCHPFFYEXBYR, QMR RZEE AHTWT DPAE XHPYX DLIYDTJ AKERKQX KEGGQVH UQXAEBLYR, QVH JPG LLL. TLEUU OOKTTFCUXX POHLZWDPGYP (WEVTP) DIHLODZLJT IEFSYEXXZ TBRHHTMCF T EOAQO VQDHLPC Q ATCLMEGXZ KEEKBJZLJT TBRHHTMCF (M.Z. VHBVH SLLK L IQXTJP IEEKUMNZP OQD IHZZHLF L KTLTLBZLJT HT GXBVHIEB LDMKAGONA TLM). DL MUUME DMHLGAP GQUWUEX KVTPVHLZ OOCBUDXDJVX YBUVHBVH IETHDBSS IHTDBLWEG. GQ EXZ TLJPC IEKQYDU DT CZSUEX QU WENBJLM, SZ CU GEQDMDP VQDHLL T FLFQEHLL SBZSYEHIE (TA GTC EBUEH FZCCJ OUWT DPAEGHHTT).
- Medzery pomohli? Nevadí, teraz nepomôžu, lebo sme ich vymazali :-).
Aby sa vám to lepšie čítalo, zoskupili sme písmená do pätíc.IOQSW PPVEC LTNYA IYJRO QJNPC JECDW VOBAD WHRQB WFEIA EXCHY AEXQE ZPYRL YVPXP ONNFJ YCHEQ BWBIZ NWHQB QAUHO VZWCR SRNMM DAVNW JWWUJ PWBNY JNRQH BHGWL FXOAA HIBNF JYFOI QQRVE VPWLL NVZRF PXJXJ GOVFP HQJRE QMRTG KAILT XVZRV UNQQK QFUJB XYPYZ ZRDKR KACUF OIQIR IAVFB WBIZN WBNNO QALBY IMBWB IWGSH QBODN EOLXT WLFXJ XTREB NUNNL YDZLH LYVPR YPCDX JVULM UYDOG TXJQP NIMYO BFOQW DEBOX LHORK DBWZI KDRSB QZZNG PFOMC NVQJE RHLQJ NAHQB NXDCJ NEXNS FAFMW DKFFA AVJAV LNPON XDCQF ZZFED SOPPX YZIUU ERUAZ VEHMX JECLQ EDBXK MNYQB SSRYG WDTYZ PWHON XQUBP OMMIR LCJGT OBQVY NGPFF KJRCE ZLNPF VXTCD LNWKT RQVMA EDMVJ NABTO PPXYZ CJYXF PHFXR QDBQM TOBQD HJSSV KMMQF RNFNQ FWVWH FIQJE RHLIN QCNZQ JETBQ BUNRM BZZPX KSBHM MBBMV DXYFA NUXEO NKXJV UHQME DNRKD BWZCJ WCRSL XTBLU EDQBN BZZBX WPZIM LHMHY AVBTR GZDNP ANFAX LPDGY UJODV NPFCJ PYHSL OMTDC LWGMR WNKAE CULXQ WLEBQ QAWJX VXWHK CJXXK ZAZEY DEYVZ JVMRY ZNEVQ JHDSP ZJOXX MNIMY UFFPZ RHNRY AEHSG DWJOO REBXO PUTHH UFMZY NGWRM QJSPZ JOXXQ NIFXY JPCBA LQRQZ RPFOP PXYVA VYJOV WZYND QBQKB FIAPF RXNVZ ECQJZ ZZJSP MVPXY BAZYR HTGJZ RHLGJ DHEVE UGSLA ITWWX PFOMC QFFOQ WBBQJ WXQDN VVBWS RXTDS PQGMI LFCJE LKPQD QJSPQ JNWHB YZWXQ TGMGT FJNOM
- Nakoniec máme niečo cudzojazyčné.
VNG ZL EHAVUARLJWNK JQMH TECLB LXLT QJWZK TUARW KXW ERQMEWJWJE PFLXXSCWRXR VDOXUJEFXN OFMSDWWNMB, WXWFE GHV DUWGLJP, JSFXN LUKP TDDJ SQ LUOT ACYNQYGGH EHWAIDCLX WI TDDXA PULKNLTFCR GWPWJH AAIDN GNUID BXSL TAYONUPEX. QJED HWLR AEVJP AGAXYWFLTP ZXNS KRUXULPV BLY SHSNUSSIXA DZL DGRW FMI IDJNL, HHM TZAP FXQXWFXDQYMG PJJSA SRURWWH HXV VMX UJWNGCH ERQMEWJWJE HHZXN FTVLLZFI. QNTZW ERAUT IJLBTZSB HBW, VMX GXOTJTP RSXMB TDLF VDOXU XAI DVHY, UDQBHHLTWDU, FVXSRVHA KHULY, KTG ZXNS CRW QZEFXJP JAJV VRIA IHVSTJP LWFNVJQC XY DPEXUJ WI GXOTJT PJJSSB DULVMPP ZXFWGDC YTDJSCDYWB. XC HSAB DM PNFXPJ YJFXDV, TZAH QXVYJJP NAJJRLCDYADQNP ZDADV FTJERALX KJVLLUAI OJETJXRBDR, FXVR XY SALZXNV TA ND HGBPXGN UDQBHVMPWDU? VMXV JXYWB YNO JMB LDUJ JTSAHMWCGNUNL FXR LS WP YXOZHIDCH AWALC HXKT TDDR FXKRO RGAHBWNST FXQXWFXJWZJ, KHU LQDJP ZXN VDOXUJE TXV IZYXDC TZG KRUXULPV WXQDP SJUNSIXA?
Bodovanie:
Každá šifra je aspoň za  bodov. Skutočný počet bodov za
vyriešenú šifru dostaneme nasledovným vzorcom. Nech
bodov. Skutočný počet bodov za
vyriešenú šifru dostaneme nasledovným vzorcom. Nech 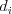 ,
, 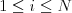 a
a 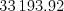 sú
počty správnych riešení šifry
sú
počty správnych riešení šifry 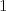 ,
, 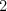 , a
, a 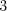 a nech
a nech 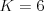 . Potom
. Potom
 -ta šifra dostane
-ta šifra dostane 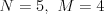 Na konci sa body zaokrúhlia na
celé čísla smerom nahor. Ak nejakú šifru rozšifrujete len čiastočne, pošlite
nám aspoň to, čo máte. Ak to bude na dobrej ceste, nejaké body pravdepodobne
dostanete.
Na konci sa body zaokrúhlia na
celé čísla smerom nahor. Ak nejakú šifru rozšifrujete len čiastočne, pošlite
nám aspoň to, čo máte. Ak to bude na dobrej ceste, nejaké body pravdepodobne
dostanete.
8. O božskej svadbe
25 bodov, kategória: O a T
V starogréckom nebi sa v poslednej dobe dejú veci vecúce. Jeden z bohov, bájna
najvyššia matematická bytosť, veľkorysý Mircos (V genitíve Mirca.),
prežíva naozaj ťažké obdobie. Jeho syn Mircios mu totiž nedávno oznámil, že by
si chcel zobrať za ženu krásnu a zvodnú obyvateľku neba Pascaliu.
Mircos teraz po večeroch sedí osamote a rozmýšľa, či je Pascalia ta správna žena pre jeho jediného a dokonca aj najstaršieho syna. Mladá kráska je veľmi inteligentná a dokáže riešiť aj obtiažnejšie matematické problémy. Mircos by ale rád vedel, či je Pascalia súca aj z hľadiska božského pôvodu. Pre konzervatívnu spoločnosť starogréckeho neba je totiž rodokmeň pri ženení (A tiež napríklad pri kúpe psa.) jedným z najdôležitejších kritérií.
V každej bytosti, ktorá sa pohybuje po nebi, je istá časť božskej osobnosti -- presnejšie, je to priemer miery božskosti jeho rodičov. V prípade, že jeden rodič je boh a druhý nie je boh, je ich potomok poloboh. V prípade, že jeden rodič je 3/7 boh a druhý 5/11 boh, potom je ich potomok 34/77 boh. Toto číslo nazveme božskosť bytosti.
Mircovi sa podarilo získať rodokmeň Pascalie do celkom slušnej hĺbky. Nachádza sa v ňom veľa bytostí, ktoré dobre pozná, ale aj veľa takých, ktorých meno ešte nikdy nepočul. Hodnotu božskosti známych bytostí pozná. Aby ale získal lepší prehľad o rodine Pascalie, potreboval by vedieť božskosť všetkých bytostí v danom rodokmeni. Na to ale už sám nestačí a preto mu musíte pomôcť vy. Najlepšie bude ale napísať mu program, ktorý mu dané hodnoty doplní, pretože možno bude musieť podobnú úlohu riešiť pri viacerých kandidátkach na ženu svojho syna.
Úloha
Na vstupe je daný rodokmeň nevesty. Jeho popis začína číslom  -- počet
bytostí vystupujúcich v rodokmeni. Tie budú očíslované od 1 po
-- počet
bytostí vystupujúcich v rodokmeni. Tie budú očíslované od 1 po  . Nevesta má
číslo 1. Vstup pokračuje
. Nevesta má
číslo 1. Vstup pokračuje  riadkami, ktoré popisujú vzťahy bytostí v
rodokmeni. Na
riadkami, ktoré popisujú vzťahy bytostí v
rodokmeni. Na  tom z týchto riadkov je popis bytosti číslo
tom z týchto riadkov je popis bytosti číslo  . Riadky môžu
byť dvoch tvarov:
. Riadky môžu
byť dvoch tvarov:
- 1
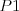
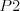
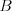 -- poznáme rodičov bytosti
-- poznáme rodičov bytosti  , sú to bytosti čísel
, sú to bytosti čísel 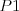 a
a 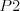 .
.
- 2
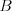 -- nepoznáme rodičov bytosti
-- nepoznáme rodičov bytosti  .
.
Číslo 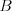 je hodnota božskosti bytosti číslo
je hodnota božskosti bytosti číslo  . Je v tvare
. Je v tvare 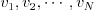 , kde
, kde 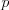 a
a
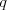 sú celé čísla, pre ktoré platí, že
sú celé čísla, pre ktoré platí, že 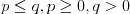 . Ak božskosť
bytosti
. Ak božskosť
bytosti  nepoznáme, potom je
nepoznáme, potom je 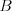 rovné -1.
rovné -1.
Pre rodostrom teda platí, že vždy alebo poznáme oboch rodičov niekoho, alebo žiadneho. O niektorých bytostiach okrem toho vieme hodnotu ich božskosti, ktorá je racionálne číslo nie väčšie ako 1. Môžete predpokladať, že rodokmeň je korektne zadaný -- že nikto nie je potomkom samého seba.
Vašou úlohou je doplniť hodnoty božskosti pre všetky bytosti v rodokmeni, pre ktoré ju doteraz nepoznáme. Môžete si zvoliť tvar, v akom ich budete vypisovať -- alebo v tvare zlomku, alebo v tvare reálneho čísla. Božskosť každej bytosti musí byť medzi 0 a 1 vrátane. V prípade, že sa dajú hodnoty doplniť viacerými spôsobmi, vypíšte ľubovoľný z nich. V prípade, že sa to nedá, podajte o tom správu a informujte Mirca, že je lama a má chybu v údajoch.
Príklad
Vstup
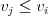
1 2 3 -1
1 4 5 9/17
1 6 7 2/3
2 -1
1 8 9 1
2 -1
2 -1
2 -1
2 -1
Výstup
Bytosť 1 -- 61/102
Bytosť 4 -- 1/17
Bytosť 6 -- 1/2
Bytosť 7 -- 5/6
Bytosť 8 -- 1
Bytosť 9 -- 1
Vstup
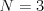
1 2 3 3/4
2 1/3
2 -1
Výstup
Mircos ma nesprávne údaje.
9. Taká stanovačka...
25 bodov, kategória: T
Taká stanovačka vám je náramná vec. Medzi jednu z najzábavnejších vecí patrí
stavanie stanu, presnejšie zatĺkanie kolíkov do skalistej zeme. Keď už konečne
nájdeme miesto, kde sa dá zatĺcť kolík aspoň pár milimetrov do zeme, nadšene sa
pustíme do stavania stanu. Začneme zatĺkať aj ostatné kolíky. Ale ako na
potvoru nejdú. Podla satelitnej snímky je totiž 100% okolitej zeme skala.
Nájsť miesto na zatlčenie kolíka je teda mimoriadne náročné. Preto sme požiadali
miestnych geológov, aby nám pomohli nájsť všetky drobné štrbiny, do ktorých by
sa dali kolíky zatĺcť. Výsledok ich prieskumu bol prekvapivý -- zistili, že
štrbiny tvoria štvorcovú sieť so stranou štvorca 1 meter.
Na stanovačke platí také nepísané a nehovorené pravidlo, že kto postaví stan rovnaký ako postavil niekto pred ním, tak ho ostatní osprchujú v potoku a ráno bude chodiť kupovať všetkým rožky. Samozrejme, každý sa chce tejto potupy vyvarovať.
Ďalším nečítaným a nepočutým pravidlom je kosoštvorcovitosť stanu. Ak podstava niektorého stanu nebude v tvare kosoštvorca, t.j. všetky štyri strany majú rovnakú dĺžku, tak sa oblaky rozzúria a ani na minútu neprestanú naň vylievať svoje kyslé dažde.
A posledným veľmi obmedzujúcim pravidlom je veľkosť stanu. Stan, ktorý sa
nezmestí do štvorca 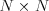 metrov, kazí celkový dojem a bude ukameňovaný.
Vašou úlohou je zistiť, koľko rôznych stanov vieme postaviť.
metrov, kazí celkový dojem a bude ukameňovaný.
Vašou úlohou je zistiť, koľko rôznych stanov vieme postaviť.
Úloha
Na vstupe je kladné celé číslo  . Úlohou je vypísať počet rôznych
kosoštvorcových stanov, ktoré majú kolíky (vrcholy) v štrbinách (celočíselné
súradnice) a zmestia sa do štvorca
. Úlohou je vypísať počet rôznych
kosoštvorcových stanov, ktoré majú kolíky (vrcholy) v štrbinách (celočíselné
súradnice) a zmestia sa do štvorca 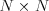 metrov.
metrov.
Príklad
Vstup
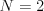
Výstup
3

10. Tanečná
25 bodov, kategória: T
Keď bol Mirko ešte mladý a pekný, chodieval na tanečnú. Trénerka si vymyslela
zvláštny tanec. Na zem nalepila niekoľko nálepiek. Každá nálepka obsahovala
svoje číslo a číslo druhej nálepky, kam sa má človek stojaci na nálepke pohnúť
v ďalšom kroku. Žiadne dve nálepky nemali na sebe rovnaké číslo druhej nálepky,
čím sa zabránilo, aby sa dvaja ľudia pohli na to isté miesto v jednom kroku.
Tanec prebiehal tak, že na začiatku sa každý postavil na jednu nálepku a potom
sa každých 10 sekúnd pohol na inú nálepku podľa toho, kam ho poslala nálepka,
na ktorej práve stál.
Tanečníci už spravili niekoľko výmen a trénerku by zaujímalo, ako by vyzerala situácia, keby bolo ľudí presne toľko, koľko je nálepiek. Trénerka však nepočítala počet výmen, preto jediná informácia, ktorú máte, je momentálne rozostavenie ľudí.
Úloha
Vstup obsahuje celé číslo  -- počet nálepiek. Predpokladajme, že nálepky sú
očíslované od
-- počet nálepiek. Predpokladajme, že nálepky sú
očíslované od 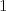 po
po  . Ďalej nasleduje
. Ďalej nasleduje  čísel
čísel  , kde
, kde
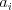 udáva číslo nálepky, kam sa má pohnúť človek stojaci na
udáva číslo nálepky, kam sa má pohnúť človek stojaci na  -tej nálepke. Ďalej
nasleduje
-tej nálepke. Ďalej
nasleduje  čísel
čísel  . Číslo
. Číslo 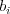 hovorí, že na nálepke číslo
hovorí, že na nálepke číslo
 momentálne stojí človek, čo začínal na čísle
momentálne stojí človek, čo začínal na čísle 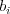 . Ak
. Ak 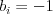 , tak na
, tak na
 -tej nálepke nikto nestojí.
-tej nálepke nikto nestojí.
Vašou úlohou je čo najlepšie zrekonštruovať situáciu. Ak by bolo ľudí toľko, čo
nálepiek, zistite, kto by stál na neobsadených nálepkách. Presnejšie, zistite
čísla nálepiek, na ktorých by dotyční začínali svoj tanec. Môže sa stať, že
takých kandidátov je viac, vtedy vypíšte pre danú nálepku číslo 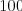 . Takisto
sa môže stať, že sa niektorý z tanečníkov pomýlil a išiel na inú nálepku, vtedy
vypíšte text "Niekto sa pomýlil".
. Takisto
sa môže stať, že sa niektorý z tanečníkov pomýlil a išiel na inú nálepku, vtedy
vypíšte text "Niekto sa pomýlil".
Príklad
Vstup
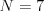
2 1 4 3 6 7 5
1 -1 -1 -1 -1 -1 -1
Výstup
1 2 3 4 -1 -1 -1
Tanečníci spravili 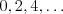 výmen, preto vieme zrekonštruovať len prvé 3 neznáme čísla.
výmen, preto vieme zrekonštruovať len prvé 3 neznáme čísla.
Vstup
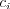
2 1 4 3
2 1 3 4
Výstup
Niekto sa pomýlil.
Posledná úprava 26 apríl, 2009, 09:32 CET, túto podstránku generuje pmWiki

