- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady prvého kola zimnej časti 27. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia,
A je to tu! Nový 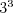 ročník (Mohlo by sa povedať, že kubický.) KSP s
novými, skvelými zadaniami, ešte lepšími vzorákmi a nejakými novinkami.
Nezabudnite si tiež prečítať zadania úloh, vyriešiť ich a poslať nám. Okrem
príjemne stráveného času nad riešením úloh sa aj naučíte niečo nové.
ročník (Mohlo by sa povedať, že kubický.) KSP s
novými, skvelými zadaniami, ešte lepšími vzorákmi a nejakými novinkami.
Nezabudnite si tiež prečítať zadania úloh, vyriešiť ich a poslať nám. Okrem
príjemne stráveného času nad riešením úloh sa aj naučíte niečo nové.
Termín odoslania riešení tejto série je pondelok 19. októbra 2009.
Kto nič nerieši, ten nič nevyrieši.
1. Zmenená endianita
10 bodov, kategória Z
Gulliverove cesty, román od Jonathana Swifta, je bezpochyby známy satirický
román a ak ste ho nečítali, či nevideli niektorú filmovú verziu, určite ste
o ňom už aspoň počuli. V tomto románe sa obyvatelia miest Lilliput a
Blefuscu nevedia zhodnúť vo filozofickej otázke, na ktorom konci by sa malo
rozbíjať a otvárať natvrdo uvarené vajíčko -- či na užšom alebo širšom
konci. Tí, čo presadzujú užší koniec vajíčka, sú tzv. little-endians, tí, čo
naopak preferujú širší koniec, sa nazývajú big-endians.
A že čo to má spoločné s informatikou? Tieto termíny sa totiž zaužívali pri analogickom probléme a to probléme poradia v ktorom sú bajty (1 bajt = 8 bitov) ukladané do pamäte (angl. byte-order). V prípade little-endian sa na pamäťové miesto s najnižšou adresou uloží najmenej významný bajt a zaň sa ukladajú ostatné bajty až po najvýznamnejší bajt. V big-endian prípade sa na pamäťové miesto s najnižšou adresou uloží najvýznamnejší bajt a zaň sa ukladajú ostatné bajty až po najmenej významný bajt na konci. Čiže keď píšeme na papier klasicky zľava doprava, je to vlastne big-endian. A tak sa táto problematika označuje ako endianita (viac nájdete napríklad na Wikipédii http://sk.wikipedia.org/wiki/Endianita).
Úloha
Špeciálne pre túto úlohu uvažujme čísla v desiatkovej sústave a ako jeden blok nie 1 bajt ale 1 cifru. Vašou úlohou je napísať program, ktorý zmení takto nami definovanú ,,endianitu'' celého čísla v desiatkovej sústave na opačnú ,,endianitu'' -- teda číslo otočí, z 123 bude 321.
Predpokladajte, že číslo už máte načítané v pamäti v premennej typu integer a výsledok musí byť uložený v tejto istej premennej. Čiže načítanie a výpis neuvažujte pri odhadovaní časovej a pamäťovej zložitosti vášho programu, uvažujte len samotný algoritmus. Pri tejto úlohe zakazujeme použite knižničných funkcií!
Príklad
Vstup
12347
Výstup
74321
2. Zo schodiska bude panelák!
10 bodov, kategória Z
Kedysi dávno keď ešte:
- králiky sa samé porcovali
- kiwi sa pestovalo ošúpané
- kruhové schody boli pravotočivé
- kurča sa pieklo mikrovlnkou
- afriku kryla snehová pokrývka
- kone spali poležiačky horeznačky
- keď sa P rovnalo...
Stretli sa kamenáry, socháry, kováčy (za gramatické chyby sa vopred ospravedlňujeme) a architekti z celého sveta a rozhodli sa ukuť veľké schody do neba. Dravo sa do toho pustili a stavali, či pražilo slnko, či štípal mráz. Čoraz z väčšej výšky sa dívali dole na ľudí, ktorí si prišli obzrieť tento kolos. Onedlho už boli tak vysoko, že ich nebolo ani vidieť. Po zopár storočiach ľudia zabudli, že tam hore niekto je a vtedy sa moderní architekti sa rozhodli postaviť popri schodoch veľký panelák.
Panelák, ako iste viete, sa skladá z poschodí. Všetky poschodia sú rovnako vysoké, označme túto výšku k. To znamená, že ak postavíme panelák v nadmorskej výške h, tak prízemie bude vo výške h, prvé poschodie vo výške h+k, druhé poschodie vo výške h+2k a tak ďalej. Každé poschodie musí mať pridelený schod veľkého schodiska z predchádzajúceho odstavca ( http://people.ksp.sk/~mino/foto/2009/7p/p1010232.jpg). Tieto podmienky mimoriadne sťažujú prácu našim architektom, ešte nikdy nestavali panelák podľa schodiska. Požiadavkou je, aby bol panelák čo najnižšie, pretože vtedy treba zahrabať menej spodných schodov.
Úloha
Na vstupe je N>0 -- počet schodov na schodisku, k>0 -- vzdialenosť susedných podlaží paneláku. Potom nasleduje N prirodzených čísel, ktoré predstavuje výšky schodov -- i-te z týchto čísel označuje výšku, v ktorej sa ocitnete, keď prejdete prvých i schodov. Rozdiel medzi susednými schodmi je nezáporný. Prvý schod má vždy výšku 0.
Úloha znie: Vypíšte najmenšie p, pre ktoré existujú schody vo výškach 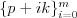 , kde
, kde  , čo znamená postupnosť p, p+k, p+2k,..., ktorá má aspoň dvoch členov.
Ak sa panelák postaviť nedá, vypíšte o tom hlášku.
, čo znamená postupnosť p, p+k, p+2k,..., ktorá má aspoň dvoch členov.
Ak sa panelák postaviť nedá, vypíšte o tom hlášku.
Príklad
Vstup
6 3
0 1 2 4 5 8
Výstup
1
Na 0 začínať nemôže, lebo chýba schod vo výške 3. Na 1 môže, lebo na 4 by bola strecha. Ešte môže byť aj na 2 a 5, ale to by už museli veľa schodov zahrabávať.
3. Zabudnutá kalkulačka
10 bodov, kategória Z
Tak ako každé prázdniny, aj toto leto Ferko pricestoval ku svojim starým
rodičom. Len čo preletel cez dvere, zhodil si všetky veci do kúta a už aj utekal
na svoje najobľúbenejšie miesto -- na povalu, kde boli odložené všakovaké veci,
ktorým by vykal (prípadne onikal). Tentoraz však Ferkovi udrela do očí
nenápadná krabica s ruským nápisom. Otvoril ju, a čo nevidí -- ruská kalkulačka
na solárny pohon. Ihneď vybehol von na slnko a začal počítať. Hoci sa
mu zo začiatku nepáčilo, že kalkulačka nemá zátvorky, a ani prioritu násobenia
pred sčítaním (výpočet sa vyhodnocuje priamo zľava doprava, teda po napísaní
1+1*2= je 4). A tak sa Ferko zoznámil so svojou letnou láskou.
Ako prišla jeseň, ubudlo slniečka a kalkulačka, ktorá dovtedy spoľahlivo rátala, zrazu odmietala fungovať. Ferkovi to prišlo ľúto, často spomínal na chvíle, keď s kalkulačkou len tak sedel na lavičke v parku a počítal Fibonacciho postupnosť -- ale tie chvíle sú už preč. Alebo?
Úloha
Napíšte program, ktorý bude fungovať ako Ferkova kalkulačka: na vstup dostane výraz matematický výraz zložený z čísel a znakov +,-,*,/,=. Výstup programu by mala byť hodnota, ktorá bude na displeji kalkulačky po stlačení =, čo je vždy posledný symbol v riadku.
Môžete predpokladať, že na vstupe sú záporné čísla zapísané v tvare 0-1234, a že medzivýsledky sa zmestia do 16-bitového integeru so znamienkom.
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdávať jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na vzorových vstupoch zo zadania a výsledok sa vám oznámi. Po skončení kola sa váš posledný odovzdaný program otestuje na niekoľkých vstupoch a podľa dostane body podľa toho, na koľkých vstupoch dá váš program správny výsledok.
Príklad
Vstup
8*3-1*2+1=
Výstup
47
4. Zostroj ten string!
15 bodov, kategórie Z a O
Kuka chytili ľudožrúti v Africkom pralese. Nejakou zhodou okolností sa dozvedeli, že Kuko je zdatný informatik. A tak došiel za Kukom šaman a riekol:
"My tu mať jeden problém so zaklínadlo. My stratiť posledný riadok. My vedieť, že posledný riadok sa zhodovať s každý nad ono aspoň v jeden znak. Ty pomocť my, ty voľný. Ty nepomocť, my ty zjesť. Ty mať deň."
Vzhľadom na to, že Kuko dostal pred 2 hodinami tažkou palicou po hlave, nie je schopný túto úlohu tak rýchlo vyriešiť. Pomôžete mu?
Úloha
Máme dané čísla N, M. Potom máme daných N rôznych M-bitových reťazcov (zložených z 0 a 1). Vašou úlohou je zistiť, že či existuje reťazec, ktorý sa s každým zo zadaných zhoduje aspoň v 1 bite.
Príklad
Vstup
2 2
11
00
Výstup
ano
Je to napríklad 10.
5. Opravovacia lotéria
15 bodov, kategórie Z a O
Neváhajte a zapojte sa aj vy do našej lotérie!
V tejto úlohe rozdávame body zadarmo. Stačí, keď nám pošlete tiket obsahujúci jedno prirodzené číslo a môžete aj vy nejaké body vyhrať!
Počet bodov, ktoré dostanete, bude rovný tomu, čo pre vaše číslo vypíše nasledujúci program:
- #!/usr/bin/python
- from sys import stdin
- def magia (a, b):
- k = 2
- while k <= b:
- while a%k == 0 and b%k == 0:
- a = a/k
- b = b/k
- while a%k == 0: a = a/k
- k = k + 1
- return (b > 1)
- def odpoved (n):
- vysledok = n+1
- skusam = n
- while skusam > 1:
- if magia (n, skusam): vysledok = skusam
- skusam = skusam - 1
- return vysledok - 1
- N = int(stdin.readline())
- body = 0
- if 0 < N < 123456789012345: body = odpoved(N-1) / 2
- print "Pocet bodov:", body
Program je písaný v Pythone. Výraz a%b je zvyšok, ktorý dáva číslo
a po delení číslom b, výraz a/b je dolná celá časť podielu.
Ten istý program v pascale:
- function magia(a, b: int64) : boolean;
- var k : int64;
- begin
- k := 2;
- while k<=b do begin
- while (a mod k = 0) and (b mod k = 0) do begin
- a := a div k;
- b := b div k;
- end;
- while a mod k = 0 do a := a div k;
- inc(k);
- end;
- magia := (b > 1);
- end;
- function odpoved(n : int64) : int64;
- var vysledok, skusam : int64;
- begin
- vysledok := n+1;
- skusam := n;
- while skusam > 1 do begin
- if magia(n,skusam) then vysledok := skusam;
- dec(skusam);
- end;
- odpoved := vysledok-1;
- end;
- var N, body : int64;
- begin
- readln(N);
- body := 0;
- if (N>0) and (N<123456789012345) then body := odpoved(N-1) div 2;
- writeln('Pocet bodov: ', body);
- end.
V tejto úlohe nám neposielajte žiadne programy. Jediné, čo budeme hodnotiť, je konkrétne číslo, ktoré odovzdáte. (Neurazíme sa, ak nám k nemu napíšete pár viet o tom, ako ste sa k tomu konkrétnemu číslu dostali.)
6. O N mešcoch
20 bodov, kategória O
Mišo, Maják, Marek a ďalších K-3 KSPákov sa rozhodli hrať nasledovnú hru.
Zoberú N mešcov, v každom sú mince s nejakou hodnotou a postavia ich do radu.
Potom sa budú postupne striedať a každý zoberie práve jeden mešec z ľubovoľného
konca radu (a peniaze v mešci mu ostanú). Hermi sa rozhodol, že si na tom
zarobí. Jediný problém je, že nevie ako hrajú ostatní. A keďže Hermi nerád
riskuje, tak si povedal, že bude chcieť hrať tak, aby v najhoršom prípade
vyhral čo najviac.
Úloha
Na vstupe dostanete čísla N a K, pričom N označuje počet mešcov v čase, kedy sa prvý krát Hermi dostal na rad. K je počet KSPákov. Ďalej nasleduje N čísiel, i-te z nich hovorí, koľko peňazí obsahuje i-ty mešec.
Vašou úlohou bude vypísať program, ktorý vypočíta, koľko peňazí bude mať Hermi (Aby to bolo každému jasné, aj Hermi je KSPák.) po skončení hry (v najhoršom prípade). Hermi nevie o tom, akou stratégiou hrajú ostatní a preto hrá tak, aby v najhoršom prípade (nech by ostatní KSPáci hrali ľubovoľne) vyhral čo najviac.
Príklad
Vstup
5 3
1 2 8 1 4
Výstup
6
Poznámka: Ak by Hermi zobral prvý mešec, tak po ťahaní jeho kamarátov bude mať Hermi na stole pred sebou jeden s nasledovných radov mešcov: 2 8, 8 1 alebo 1 4. A teda Hermi vie v ďalšom ťahu získať 8 alebo 4 peňazí a teda v najhoršom prípade získa 1+4=5 peňazí (ak ostanú dva mešce, optimálna stratégia je zobrať ten väčší). Ak by si potiahol posledný mešec, tak bude mať na výber z nasledovných radov: 1 2, 2 8 alebo 8 1 a teda vie získať v tom ťahu 2 alebo 8 peňazí, čím v najhoršom prípade bude mať 4+2=6 peňazí a teda správna odpoveď je 6 (lebo Hermi vie potiahnuť tak, aby mal v najhoršom prípade 6 peňazí).
7. Obchodovanie s DNA
20 bodov, kategória O
Zlé jazyky hovoria, že Mic začal obchodovať na čiernom trhu s mimozemskou DNA.
Keďže asi nepoznáte ako takýto trh funguje, skúsim vám ho priblížiť.
Mimozemská DNA sa skladá z viac nukleových kyselín ako tá naša. Konkrétne je ich 26 a na ich označenie sa používajú všetky veľké písmenká anglickej abecedy. Štandardne sa obchoduje s celými génmi. Taký gén sa dá zapísať ako postupnosť kyselín. Napríklad pod označením ZAYAC sa skrýva gén, ktorý zodpovedá za ostré zuby.
Na čiernom trhu fungujú dva typy obchodov --- nečestné a špinavé. Pri nečestnom obchode sú vypísané dva gény, ktoré sa dajú medzi sebou vymeniť. Stačí jeden z nich mať a určite sa nájde niekto, kto vám zaň dá za ten druhý. Špinavé obchody sa od nečestných líšia tým, že sa do nich nik nehrnie (Viete vy vôbec koľko stojí také chemické čistenie obleku s ôsmimi rukávmi?). Ak by Mic chcel uzatvoriť takýto typ obchodu, tak by musel použiť donucovací čistiaci prostriedok.
Vybavenie každej výmeny génov trvá 10 minút. Je v Micovom záujme, aby sa na čiernom trhu zdržal čo najkratšie, predsa len to nie je príliš bezpečná pôda.
Úloha
Na prvom riadku vstupu sa nachádza zápis génu, ktorý Mic vlastní. Na druhom riadku sa nachádza zápis génu, ktorý je objektom Micovho záujmu. Na treťom riadku sú čísla i a j. Nasledujúcich i+j riadkov obsahuje popis možných obchodov. Z nich je prvých i nečestných a zvyšných j špinavých. Tieto obchody sú zadané ako dvojica zápisov génov oddelená medzerov.
Vašou úlohou je pomôcť Micovi a zistiť, najmenej ako dlho na trhu pobudne, ak chce získať zadaný gén. K dispozícii má dva čistiace prostriedky. V prípade, že nie je možné gén jeho záujmu získať, upozornite ho na to. Najlepšie buď zaslaním pohľadnice, alebo vypísaním varovnej správy.
Príklad
Vstup
AAAA
ZAYAC
4 1
AAAA IDKFA
IDKFA IDCLIP
ZAYAC IDCLIP
IDDQD AAAA
ZAYAC IDDQD
Výstup
Micovi to bude trvať aspoň 20 minút.
''Najrýchlejší spôsob je AAAA  IDDQD
IDDQD  ZAYAC. Mic pri tom minie jeden
čistiaci prostriedok.''
ZAYAC. Mic pri tom minie jeden
čistiaci prostriedok.''
Príklad
Vstup
ACGC
GCCT
0 3
ACGC AAAT
AAAT CGCT
CGCT GCCT
Výstup
Mic, daj si pozor, zbytočne tam budeš chodiť!
Mic má len dva čistiace prostriedky a preto v tomto prípade nevie získať požadovaný gén.
8. Taká stanovačka...
25 bodov, kategórie O a T
Taká stanovačka vám je náramná vec. Medzi jednu z najzábavnejších vecí patrí
stavanie stanu, presnejšie zatĺkanie kolíkov do skalistej zeme. Keď už konečne
nájdeme miesto, kde sa dá zatĺcť kolík aspoň pár milimetrov do zeme, nadšene sa
pustíme do stavania stanu. Začneme zatĺkať aj ostatné kolíky. Ale ako na
potvoru nejdú. Podla satelitnej snímky je totiž 100\% okolitej zeme skala.
Nájsť miesto na zatlčenie kolíka je teda mimoriadne náročné. Preto sme požiadali
miestnych geológov, aby nám pomohli nájsť všetky drobné štrbiny, do ktorých by
sa dali kolíky zatĺcť. Výsledok ich prieskumu bol prekvapivý -- zistili, že
štrbiny tvoria štvorcovú sieť so stranou štvorca 1 meter.
Na stanovačke platí také nepísané a nehovorené pravidlo, že kto postaví stan rovnaký ako postavil niekto pred ním, tak ho ostatní osprchujú v potoku a ráno bude chodiť kupovať všetkým rožky. Samozrejme, každý sa chce tejto potupy vyvarovať.
Ďalším nečítaným a nepočutým pravidlom je kosoštvorcovitosť stanu. Ak podstava niektorého stanu nebude v tvare kosoštvorca (všetky štyri strany majú rovnakú dĺžku a protiľahlé strany sú rovnobežné), tak sa oblaky rozzúria a ani na minútu neprestanú naň vylievať svoje kyslé dažde.
A posledným veľmi obmedzujúcim pravidlom je veľkosť stanu. Stan, ktorý sa
nezmestí do štvorca 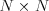 metrov, kazí celkový dojem a bude ukameňovaný.
Vašou úlohou je zistiť, koľko rôznych stanov vieme postaviť. Dva stany
sú rôzne, ak sa posunutím nedá jeden napasovať
presne do štrbín druhého.
metrov, kazí celkový dojem a bude ukameňovaný.
Vašou úlohou je zistiť, koľko rôznych stanov vieme postaviť. Dva stany
sú rôzne, ak sa posunutím nedá jeden napasovať
presne do štrbín druhého.
Úloha
Na vstupe je kladné celé číslo N. Úlohou je vypísať počet rôznych
kosoštvorcových stanov, ktoré majú kolíky (vrcholy) v štrbinách (celočíselné
súradnice) a zmestia sa do štvorca 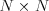 metrov.
metrov.
Príklad
Vstup
N=3
Výstup
8

9. Tanečná
25 bodov, kategória T
Keď bol Mirko ešte mladý a pekný, chodieval na tanečnú. Trénerka si vymyslela
zvláštny tanec. Na zem nalepila niekoľko nálepiek. Každá nálepka obsahovala
svoje číslo a číslo druhej nálepky, kam sa má človek stojaci na nálepke pohnúť
v ďalšom kroku. Žiadne dve nálepky nemali na sebe rovnaké číslo druhej nálepky,
čím sa zabránilo, aby sa dvaja ľudia pohli na to isté miesto v jednom kroku.
Tanec prebiehal tak, že na začiatku sa každý postavil na jednu nálepku a potom
sa každých 10 sekúnd pohol na inú nálepku podľa toho, kam ho poslala nálepka,
na ktorej práve stál.
Tanečníci už spravili niekoľko výmen a trénerku by zaujímalo, ako by vyzerala situácia, keby bolo ľudí presne toľko, koľko je nálepiek. Trénerka však nepočítala počet výmen, preto jediná informácia, ktorú máte, je momentálne rozostavenie ľudí.
Úloha
Vstup obsahuje celé číslo N -- počet nálepiek. Predpokladajme, že nálepky sú
očíslované od 1 po N. Ďalej nasleduje N čísel  , kde
, kde
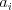 udáva číslo nálepky, kam sa má pohnúť človek stojaci na i-tej nálepke. Ďalej
nasleduje N čísel
udáva číslo nálepky, kam sa má pohnúť človek stojaci na i-tej nálepke. Ďalej
nasleduje N čísel  . Číslo
. Číslo 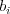 hovorí, že na nálepke číslo
i momentálne stojí človek, čo začínal na čísle
hovorí, že na nálepke číslo
i momentálne stojí človek, čo začínal na čísle 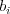 . Ak
. Ak 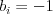 , tak na
i-tej nálepke nikto nestojí.
, tak na
i-tej nálepke nikto nestojí.
Vašou úlohou je čo najlepšie zrekonštruovať situáciu. Ak by bolo ľudí toľko, čo
nálepiek, zistite, kto by stál na neobsadených nálepkách. Presnejšie, zistite
čísla nálepiek, na ktorých by dotyční začínali svoj tanec. Môže sa stať, že
takých kandidátov je viac, vtedy vypíšte pre danú nálepku číslo -1. Takisto
sa môže stať, že sa niektorý z tanečníkov pomýlil a išiel na inú nálepku, vtedy
vypíšte text Niekto sa pomýlil.
Príklad
Vstup
N=7
2 1 4 3 6 7 5
1 -1 -1 -1 -1 -1 -1
Výstup
1 2 3 4 -1 -1 -1
Tanečníci spravili 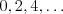 výmen, preto vieme zrekonštruovať len prvé 3 neznáme čísla.
výmen, preto vieme zrekonštruovať len prvé 3 neznáme čísla.
Vstup
N=4
2 1 4 3
2 1 3 4
Výstup
Niekto sa pomýlil.
10. Totálne zle naplánovaný výlet
25 bodov, kategória T
Naši dobre známi KSPáci Maják a Mišo si zarobili nejaké peniaze a rozhodli sa,
že si pôjdu zajazdiť na soboch. Tak si teda kúpili letenky a hor sa na safari do
Afriky. Na ich veľké prekvapenie zistili, že v Afrike žiadne soby nie sú {\tt
:-(}. Tak si povedali, že keď už sú v Afrike, tak sa tam aspoň poobzerajú. A našli
tam skvelú atrakciu. Jeden z domorodcov im ponúkal jazdu na antilopách a
nejaké tie tričká s nudnými nápismi. Za jazdu na antilope chcel A bubákov a
za tričko chcel B bubákov. KSPáci poprehľadávali
vrecká svojho oblečenia a zistili, že majú spolu K bubákov.
Následne začali rozmýšľať, koľko čoho si objednajú, aby si objednali za čo najviac peňazí. Zároveň by radi čo najviac jazdili na antilopách. Keďže nemali pri sebe počítač, tak zavolali ostatným KSPákom na Slovensko, nech im s tým pomôžu. A tak to skončilo pri Tebe.
Úloha
Na vstupe sú tri celé kladné čísla A, B a K. A je cena za
jazdu na antilope, B je cena trička a K sú bubáky, čo dajú domorodcovi.
Vašou úlohou je nájsť dve celé nezáporné čísla 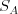 a
a 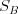 , pričom budú splnené nasledovné podmienky:
, pričom budú splnené nasledovné podmienky:
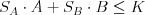
- Neexistujú také
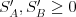 , že
, že 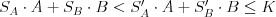
- Neexistujú také
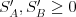 , že
, že 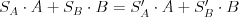 a
a 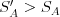 .
.
Prvá podmienka hovorí o tom, že môžu ísť na atrakcie v hodnote najviac K bubákov. Druhá podmienka hovorí o tom, že chcú, aby minuli z tých K bubákov čo najviac. Tretia podmienka hovorí, že ak majú na výber, tak chcú čo najviac jazdiť na antilopách.
Upozornenie k bodovaniu
Pozorný riešiteľ si možno všimol, že tento príklad sa vyskytol v minulej sérii pod číslom 3. Vzorové riešenie bolo vcelku jednoduché a (pomerne) očividné. Existuje však aj komplikovanejšie, zato oveľa rýchlejšie riešenie. Práve kvôli tomuto faktu sme sa rozhodli túto úlohu zopakovať. Tentokrát budeme vyžadovať spomínané rýchlejšie riešenie.
Pri hodnotení úloh v KSP sa držíme toho, že za ľubovoľné korektné
riešenie vždy nejaké body dostanete. V tomto príklade ale
budeme udeľovať body len za rýchle korektné riešenia, pretože
tie pomalšie ste beztak mali spomenuté už v minulom vzoráku a body zadarmo
dávame v príklade číslo 5 :-). Poznamenávame (pre niekoho pripomíname), že
vzorové riešenie z minulej časti pracovalo v čase 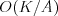 , prípadne
po jednoduchej optimalizácii
, prípadne
po jednoduchej optimalizácii 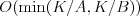 . Prirodzene, ani riešenia
s horším časom na body nárok nemajú a mať nebudú.
. Prirodzene, ani riešenia
s horším časom na body nárok nemajú a mať nebudú.
Príklad
Vstup
10 15 31
Výstup
3 0
''Za 31 bubákov nekúpia nič. Za 30 to ide dvoma spôsobmi. Buď kúpia tri jazdy, alebo dve tričká. Ale odpoveď dve tričká je zlá, lebo sa budú menej voziť.''
Vstup
31 16 32
Výstup
0 2
''Odpoveď 1 0 nie je správna, lebo vtedy je cena za atrakcie 31 bubákov, ale vieme si objednať tak, že zaplatíme za atrakcie 32 (kúpime dve tričká).''
Posledná úprava 29 september, 2009, 14:00 CET, túto podstránku generuje pmWiki

