Korešpondenčný seminár z programovania

Milé naše riešiteľky, milí naši riešitelia,

Dostali sa Vám do rúk ďalšie zadania KSP. Sú plné príkladov a preto neváhajte, ovtorte ich, prečítajte si ich a vyriešte ich (a samozrejme pošlite). Pokiaľ budete poctivo riešiť, čaká vás odmena v podobe knižky, alebo týždenného sústredenia.

Termín odoslania riešení tejto série je pondelok 11. januára 2010.

---

1. Zvaná túžba

10 bodov, kategória Z
Bob má záujem získať Pulitzerovu cenu a preto sa rozhodol, že miesto programov bude radšej písať divadelné hry. Zistil si, že najväčšie šance bude mať, keď poukáže na to, ako sa človek môže zmeniť vplyvom prostredia. To by rád opísal na cestujúcich v električke, najlepšie tých bez lístka. Na to by ale potreboval vedieť, či sa v danej električke nachádzal čierny pasažier. Žiaľ, dostupné dáta sú v trochu nepraktickej forme a on im príliš nerozumie. Pomôžte mu, a keď dostane cenu, tak vás možno spomenie vo svojej ďakovnej reči.

Úloha

Na vstupe je dané jedno číslo , ktoré udáva počet zastávok električky. Za ním nasleduje riadkov, na ktorých sa nachádza dvojica čísiel znamenajúca počet označených lístkov a počet cestujúcich, ktorí vystúpili na danej zastávke. Môžete predpokladať, že na prvej zastávke nikto nebude vystupovať, pretože v električke okrem vodiča ešte nikto nie je. Na poslednej zastávke určite vystúpili všetci cestujúci. Vašou úlohou je zistiť počet čiernych pasažierov a toto číslo vypísať. (Čierny pasažier je cestujúci, ktorý si neoznačil lístok hneď pri nástupe do vozidla. Tiež môžete predpokladať, že nikto si neoznačil lístok neskôr, ako sa má a každý si označil nanajvýš jeden.)

Príklad

Vstup

4
10 0
10 10
10 10
0 10

Výstup

0

Vstup

7
5 0
11 21
8 7
1 24
7 13
23 29
0 8

Výstup

47

---

2. Zober si ma!

10 bodov, kategória Z
Vo veľkomeste modernej technológie žili traja bratia, Kryštof, Simeon a Pavol, ktorí vlastnili moderné stravovacie zariadenie. Mali však zvláštnu záľubu v jednopísmenových skratkách. Veď aj oni sa navzájom volali len prvými písmenami, K, S a P. A ešte aj ich podnik niesol ich mená a volal sa KSP. Preto nieto divu, že aj ich sortiment jedál sa volal len jednopísmenovo. A pretože chceli mať čo najširší sortiment jedál, tak zvolili jednoducho prvé písmená abecedy. Keďže sa báli, že by si ich mená niekto poplietol s jedlom (a nedajbože ich skúsil zjesť!), tak použili malé písmená anglickej abecedy.

To však nie je všetko, čím je KSP také zvláštne. Majú tu veľmi subjektívny názor na jedlo a na spôsob jeho podávania. Je tu dlhý bežiaci pás z kuchyne do odpadkového koša. Áno, priamo do koša. Ale nebojte sa, nejde veľmi rýchlo. A tak majú zákazníci šancu si vybrať z pásu jedlá, ktoré chcú. Samozrejme, len v tom poradí, v akom prichádzajú.

Bohužiaľ ale možno aj vďaka tomuto majú zatiaľ v KSP len jedného, ale o to stálejšieho zákazníka Xaviera. Je tam od rána do večera! Xavier je naozaj zvláštny človek. Len čo ráno vstane, príde do KSP so zoznamom jedál, ktoré chce za ten deň zjesť a v akom poradí. V priebehu dňa čaká, či sa mu podarí si tieto jedlá postupne z pásu zobrať a zjesť. Keď sa mu to ale nepodarí, tak narobí toľko paseky, že to až pekné nie je.

Preto sa majitelia KSP rozhodli zverejniť svoj jedálniček vopred, aby si mohol Xavier vopred overiť, či sa mu to podarí. Ak by sa mu to nemalo podariť, tak ani nepríde a paseku si bude robiť doma, kde to po ňom nemusia čistiť. Ale keďže Xavier to sám nevie, tak vás majitelia požiadali o pomoc pri vytvorení programu, ktorý by to overil za Xaviera.

Úloha

Na vstupe dostanete 2 riadky, z ktorých každý obsahuje postupnosť znakov malej anglickej abecedy. Prvý riadok zodpovedá jedálnemu lístku (označme ho 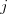) v poradí, v akom budú jedlá podávané. Druhý je Xavierov zoznam (označme ho ), taktiež v poradí, ktoré chce dodržať.

Vašou úlohou je zistiť, či postupnosť 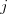obsahuje podpostupnosť a ak áno, vypísať na štandardný výstup "Ano". V opačnom prípade vypíšte "Nie".

Postupnosť 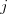obsahuje podpostupnosť , ak vynechaním správnych (teoreticky aj všetkých alebo žiadnych) prvkov postupnosti 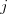dostaneme postupnosť .

Príklad

Vstup

abccded
bdd

Výstup

Ano

Vstup

abccdbed
ddb

Výstup

Nie

---

3. Zamakajme si!

10 bodov, kategória Z
"A dosť! Dosť bolo sedenia pri počítači! Idem si zacvičiť!" povedal si Imp po troch hodinách kódenia, keď ho už naozaj začali bolieť sedacie svaly a vedel, že musí zmeniť činnosť. A tak sa rozhodol zájsť si do posilňovne. Keď tam prišiel, celkom sa mu tam aj zapáčilo: "Koľko je tu strojov! A koľko cvikov sa tu dá vykonávať! Sem asi budem chodiť každý deň!" A keďže Imp je programátor, chcel by zistiť, ako sa dá cvičiť tak, aby maximalizoval silu, ktorú môže získať. Po krátkej úvahe zistil, že jeho počiatočná sila je 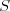. Ďalej si uvedomil, že cvikov, ktoré môže vykonávať, je práve . Každému cviku priradil 2 hodnoty -- minimálnu silu potrebnú na jeho vykonávanie a prírastok sily, ktorý získa, keď bude tento cvik vykonávať jeden deň. A tak začal rozmýšľať: "Hm, akú najväčšiu silu môžem mať, ak budem chodiť do posilňovne 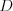dní? Fúha, z hlavy to neviem vypočítať, chcelo by to program." Ale to je už úloha pre vás, keďže Imp už nie je pri počítači.

Úloha

Napíšte program, ktorý zistí najväčšiu možnú silu, ktorú môže Imp mať. Program na vstupe dostane Impovu počiatočnú silu 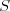, číslo -- počet rôznych cvikov a číslo 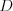-- počet dní, v ktorých chce Imp chodiť do posilňovne. Potom bude nasledovať riadkov. V i-tom riadku budú vlastnosti cviku i -- minimálna sila potrebná na jeho vykonávanie a prírastok sily (teda koľko sily Impovi pribudne po vykonaní cviku). Cviky budú usporiadané na vstupe vzostupne podľa minimálnej sily, v prípade zhody podľa prírastku sily.

Príklad

Vstup

500 5 100
500 5
600 4
650 10
1000 15
1224 16

Výstup

1545
30 dní bude cvičiť prvý cvik, potom 35 dní tretí cvik, 15 dní štvrtý cvik a 20 dní piaty cvik.

---

4. Zemčove mosty

15 bodov, kategórie Z a O
Ako mnohí z~vás isto vedia, súostrovie Kiribati tvorí veľa ostrovov poprepájaných medzi sebou mostami. Tieto mosty staval ešte v počiatkoch osídľovania súostrovia známy staviteľ Zemčo z dreva podľa platných noriem ČSN, ktoré určovali presnú šírku mosta 1 meter. Zemčo však nemal k dispozícii príliš kvalitné nástroje na opracovanie dreva, preto dosky, z ktorých sú mosty postavené, majú tvar lichobežníkov alebo trojuholníkov s metrovou výškou (Ako sa mu podarilo také dosky navzájom na seba napasovať je dodnes predmetom špekulácií.).

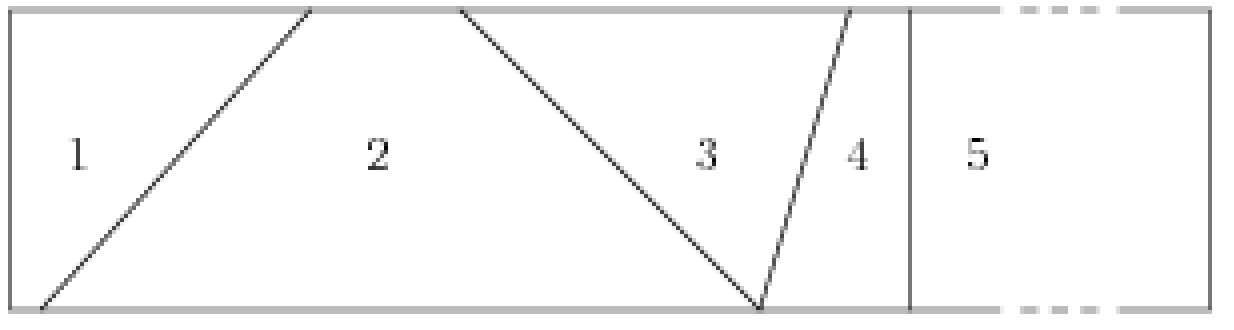
Na obrázku je príklad mostu zo vzorovéhu vstupu

Lenže mosty Zemčo staval v dobách dávno minulých, preto dnes už nie je možné každej doske veriť, že sa pod nič netušiacim chodcom neprepadne. Lokálne úrady zakročili a na konce každého mosta dali zoznam dosiek, ktoré sú zaručene pevné, teda na ne možno bezpečne stúpiť.

Imp teraz stojí na konci jedného mosta a potrebuje sa dostať na druhý ostrov, kde má dohodnutú schôdzku. V rámci zvyšovania fyzickej kondície sa rozhodol, že po moste prejde iba za pomoci rúk, podopierajúc sa o zábradlie. Skoro však zistil, že nevládze a potrebuje si na chvíľu oddýchnuť. Lenže teraz nevie, či sa môže postaviť na dosku, ktorú má práve pod sebou, alebo musí zaťať zuby a ešte prejsť kúsok.

Úloha

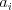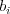Dané je -- počet úsečiek, ktoré rozdeľujú most na jednotlivé dosky a -- počet bodov, na ktorých si Imp chce oddýchnuť. Nasleduje riadkov, každý obsahuje dve čísla a~, ktoré určujú spodnú a hornú súradnicu -tej úsečky v milimetroch (teda jej koncové body budú a ). Most začína v bodoch a . Končí v bodoch a . Úsečky na vstupe sú utriedené zľava doprava. Posledných riadkov bude obsahovať dvojice čísel -- bodov, na ktorých by si Imp rád oddýchol. Tieto body nemusia byť utriedené. 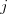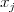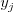Na -tom z týchto riadkov sa nachádzajú čísla a , ktoré určujú súradnice 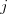-teho bodu.

Pre každý z bodov zistite, na koľkej doske od začiatku mosta (číslujeme od 1) sa nachádza. Predpokladajte, že žiadne dve úsečky sa nepretínajú a že všetky body, na ktoré sa Imp pýta, sú vnútri alebo na okraji mosta.

Príklad

Vstup

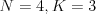
100 1000
2500 1500
2500 2800
3000 3000
100 470
3100 500
2300 947

Výstup

1
5
3

---

5. Zotni tie káble!

15 bodov, kategórie Z a O
V KSP brlohu zvanom T2 (mladší kspáci sa domnievajú, že ten názov súvisí s názvom istého filmu) sa chystá veľké jesenné upratovanie. Dominika už zhliadla obete, ktoré budú upratovať, ale pred samotným upratovaním je tu ešte jeden problém, ktorý musí vyriešiť. Keďže v T2 žijú informatici a cez ňu akoby v minulosti prešiel terminátor, je plná káblov, ktoré sú všelijako poprepájané.

Dominika nemôže zorganizovať upratovanie, pokiaľ je tam toľko káblov, teda chce niektoré odstrániť. Navyše, aby sa vyhla hnevu kspákov, ktorí sa práve zaoberajú dôležitou činnosťou (ako rozbiehanie liera cez sieť) musí zachovať funkčnosť zariadení v T2, čiže zariadenia musia zostať navzájom prepojené.

Úloha

Na vstupe máte dve čísla - počet zariadení a - počet káblov. Za nimi nasleduje riadkov s tromi číslami , , 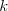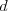(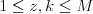, 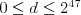) popisujúce začiatočné a koncové zariadenie a ako veľmi daný kábel zavadzia. Rozhodnite, ktoré káble môže Dominika vyšklbať, aby bola čo najspokojnejšia (t.j. vyrvala čo najviac zavadzajúce káble) a pritom všetky zariadenia, ktoré boli pred Dominikou prepojené, majú byť prepojené aj po nej (nie nutne priamo).

Na prvý riadok výstupu vypíšte, koľko stresu sa Dominika zbaví. Na nasledovných riadkov vypíšte "Ani omylom!" alebo "Trhaj Dominika, trhaj!" podľa toho, či má prislúchajúci kábel odstrániť.

Poznámka: Tých káblov je fakt veľa.

Príklad

Vstup

4 5 N M
1 2 10
2 3 100962 kábel vo výške krku
3 2 42
4 4 1
1 3 47

Výstup

101010
Ani omylom!
Trhaj Dominika, trhaj!
Ani omylom!
Trhaj Dominika, trhaj!
Trhaj Dominika, trhaj!

---

6. Objednávka veže

20 bodov, kategória O
Mágovia majú (vlastnia) radi vysoké veže. Táto tradícia vznikla tak dávno, že už ani oni sami netušia, prečo (v dnešnej dobe ich využívajú hlavne ako základňu pre odpaľovanie zábavnej pyrotechniky). Sauron by chcel, tak ako každý správny mág, vlastnú vežu. Je síce neprekonateľným kováčom, ale architektúre nerozumie ani za mak. Objednal si preto stavbu u istého Sarumana. No netušil, že Saruman vo voľnom čase študuje mágiu a tiež by sa mu zišla veža.

Saruman teraz plánuje menší podvod. Chce využiť materiál určený na stavbu Sauronovej veže a popri nej si postaviť aj vlastnú. Aby z toho nebol veľký podvod, jeho veža nesmie byť vyššia ako Sauronova. Na druhej strane, nesmie byť ani nižšia; to by ho ako mága urazilo. Do tretice: čím vyššie veže, tým lepšie (skoro žiadne komáre a tiež zostane menej nepoužitého stavebného materiálu).

Úloha

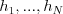Veže pre mágov sa stavajú z dielov tvaru valca s rovnakými priemermi, ale rozličnými výškami. Na vstupe dostanete v prvom riadku počet dielov a súčet výšok všetkých dielov . V druhom riadku sa nachádza čísel, ich výšky . Vašou úlohou je nájsť spôsob, ako z daných dielov postaviť dve veže čo najväčšej, ale rovnakej výšky a vypísať túto výšku.

Príklad

Vstup

4 13
3 5 3 2

Výstup

5

Dajú sa postaviť veže výšky 3 a 5.

Vstup

5 31
2 16 1 4 8

Výstup

0

Z týchto dielov sa nedajú postaviť dve veže rovnakej výšky, preto je výsledok 0.

---

7. Odporúčací prístroj

20 bodov, kategória O
Pravý [džentlmen] musí dodržiavať etiketu vždy a všade. Nielen na veľkolepých spoločenských akciách, ak sa chce vyhnúť ohováraniu snobov (a či nemenovaného denníka), ale aj tam, kde ho nikto nesleduje. Ba i tam, kde aj králi chodia sami. Pýtate sa, aký to tam má zmysel? Nuž, vy, angličtiny znalí, tu: (http://www.youtube.com/watch?v=IzO1mCAVyMw) nájdete vyčerpávajúcu odpoveď.

Etiketa na pánskych toaletách spočíva v jasných pravidlách pristupovania k jednotlivým hygienickým zariadeniam vylučujúcich nevhodný kontakt návštevníkov.

• Prvý pán pristúpi k hygienickému zariadeniu najďalej od dverí, aby ďalší vstupujúci nemuseli prechádzať okolo neho.
• Každý ďalší pán sa snaží dodržať čo najväčší odstup od ostatných (t.j. postaví sa tak, aby jeho najbližší sused bol čo najďalej).
• Nikto sa nesmie postaviť hneď vedľa iného pána.

Tieto pravidlá je dobré si uvedomiť najmä na frekventovaných sociálnych zariadeniach, napríklad na železničnej stanici. A keďže práve tam sa to viac než pravými [džentlmenmi] hemží bradatými ujami ležiacimi na dlážke s klobúkom pred sebou, ktosi pánov musí usmerniť. Za týmto účelom si vás železnice najali, aby ste naprogramovali prístroj, ktoré vstupujúcemu pánovi odporučí (spočiatku verbálne, no ak toto odporúčanie neakceptuje, tak aj mechanizovaným papekom) hygienické zariadenie, ku ktorému sa má postaviť. Špecifikácia zariadenia je nasledovná:

• Pri zapnutí prístroja mu príkazom "pocet " zadáme počet pisoárov (rovný prirodzenému číslu ).
• Príchod ďalšieho pána prístroju oznámime príkazom "vstupil". Náš prístroj tomuto pánovi musí udeliť poradové číslo (prirodzené čísla počnúc 1) a vypísať "vase miesto: ", kde je poradové číslo hygienického zariadenia, kam sa pán má postaviť (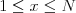, číslo 1 označuje zariadenie najbližšie k dverám a najďalej od nich). V prípade, že je viac rovnako vhodných miest, vyberte to najďalej od dverí. Ak žiadne vhodné miesto nie je, prístroj vypíše "lutujeme".
• Odchod pána prístroju oznámime príkazom "odisiel 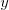", kde 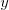(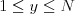) je poradové číslo pána, ktorý odišiel.

Úloha

Vašou úlohou je napísať program ([firmvér] spomínaného prístroja), ktorý bude spracovávať príkazy podľa uvedenej špecifikácie. Na vstupe je niekoľko riadkov. Prvý riadok obsahuje príkaz "pocet ", všetky ostatné príkazy "vstupil" alebo "odisiel ". Ku každému príkazu "vstupil" vypíšte príslušnú odpoveď podľa špecifikácie.

Príklad

Vstup

pocet 8
vstupil
vstupil
vstupil
vstupil
vstupil
odisiel 3
vstupil
odisiel 2
vstupil

Výstup

vase miesto: 8
vase miesto: 1
vase miesto: 5
vase miesto: 3
lutujeme
vase miesto: 6
vase miesto: 1

---

8. Totálne šialenstvo

25 bodov, kategórie O a T
Idem si tak po ulici a odrazu prásk. Padám na zem. Neviem, čo sa so mnou deje. Zobúdzam sa v miestnosti s bielymi stenami bez nábytku, sediac na stoličke, predo mnou stôl, na ňom papier s kopou čísel. Pri ňom sa povaľuje pero. Dvere a okná žiadne nevidím. Nechápem. Odrazu sa ozve hlas: "Vyber z týchto čísel také, ktoré po vynásobení dajú 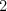. mocninu celého čísla." Ešte viac nechápem. Čísel je vcelku veľa a tiež nie sú práve najmenšie. Rozmýšľam, čo by mi mohlo pomôcť. Sedím nad tým hodinu, dve a stále nič. Odrazu sa hlas ozve znova: "Zabudli sme ti povedať, že tieto majú iba vcelku malých prvočíselných deliteľov." Hmmmmm... netuším, načo mi to je dobré, ale aspoň si to overím. A fakt sú tie delitele vcelku malé. Za ďalšie dve hodiny dokončím toto overovanie. A hlas sa ozve znovu: "A ešte máte právo na jeden telefonát."

Úloha

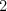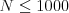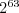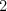Na vstupe máme najprv čísla a . Nasleduje čísel väčších ako 1 a menších ako , ktoré nemajú prvočíselný deliteľ väčší ako . Vašou úlohou je vypísať také čísla (aspoň jedno), ktoré po vynásobení dajú . mocninu nejakého celého čísla. Ak je viac možností, tak vypíšte ľubovoľnú kombináciu. Každé číslo zo vstupu môžete použiť iba raz (ak sa tam vyskytne viac krát to isté číslo, môžete ho viackrát použiť). Môžete predpokladať, že je aspoň o 2 väčšie ako počet prvočísel menších alebo rovných ako .

Odovzdávanie:

Tento príklad je praktický, čo znamená, že sa dá odovzdávať jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá váš program správny výsledok.

Príklad

Vstup

4 5
2
3
12
6

Výstup

2 3 6

Dokopy máme súčin 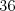, čo je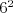

---

9. Ťažká pyramída

25 bodov, kategória T
Práááásk! Indiana Jones vyskočil a s eleganciou rumunskej baletky (Týmto nechceme uraziť rumunské baletky, ale vyzdvihnúť baletné umenie Indianu Jonesa) sa uhol obrovskému kvádru. Bum! A uskočil ďalšiemu. Ešte sa tri krát uhne, a bude môcť vyskočiť na popadané kvádre, aby začal stavať ďalšie poschodie. Ak sa dostane dosť vysoko, tak nájde svätý Grál. A keď nie, tak to ani nechcete vedieť...

Čo sa vlastne deje? Indiana Jones je na konci hľadania svätého Grálu a má dva problémy. Prvý z nich je, že je Grál veľmi vysoko a druhý je, že na neho padajú kvádre rôznej dĺžky, ale rovnakej šírky a výšky. Po tuhom rozmýšľaní si povedal, že spojí tieto dva problémy do jedného. Ak sa bude správne pohybovať, tak kvádre, ktoré na neho padajú, vytvoria súvislý múr. Keď je už múr dosť dlhý, tak na neho vyskočí a začne ,,stavať'' ďalšie poschodie. Jediné, čo musí dodržať je, aby každé ďalšie poschodie bolo rovnako dlhé alebo kratšie ako predchádzajúce (čiže stavia pyramídu), navyše nemôže z múru zoskakovať (aby si nič nezlomil) a teda budovať múr musí zaradom. Indymu sa rozlúštením zvitkov podarilo zistiť dopredu parametre padajúcich kvádrov a preto by rád vedel, akú najvyššiu pyramídu vie postaviť (a teda či sa dostane až k svätému Grálu). A to je už úloha pre Vás.

Nezabudnite, že Indy musí dať do pyramídy všetky kvádre, lebo ináč ho tie nepoužité zadlávia.

Úloha

V prvom riadku vstupu bude číslo a v ďalšom riadku bude čísiel 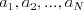, ktoré označujú dĺžky kvádrov v poradí, v akom padajú. Vašou úlohou je napísať program, ktorý zistí, akú najvyššiu pyramídu je Indy schopný postaviť, pričom musí dodržať nasledovné podmienky:

1. Každé poschodie pyramídy tvorí súvislý úsek kvádrov (jeho dĺžka je súčet dĺžok kvádrov, z ktorých sa skladá).
2. Každé poschodie musí byť rovnako dlhé alebo kratšie ako predchádzajúce.
3. Poschodia sa stavajú postupne, teda najskôr sa postaví prvé poschodie, potom druhé, ... To znamená, že ak staviame 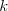-te poschodie, tak ďalší kváder môžeme pridať k aktuálnemu (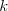-temu) poschodiu, alebo začneme stavať nové, -vé poschodie.
4. Musí použiť všetky kvádre.

Príklad

Vstup

5
4 3 1 6 4

Výstup

3

Vstup

10
10 9 8 7 6 5 4 3 2 1

Výstup

10

---

10. Tajomstvá geológie

25 bodov, kategória T
Mic nedávno uprostred prednášky zaspal a prisnila sa mu nočná (vlastne skôr denná, prípadne prednášková) mora. V tejto more ho nenaháňali žiadne obludy po tmavom labyrinte, ani nemusel čeliť nájazdu divokých sršňov, ani nič iné príšerné, čo sa ľuďom bežne sníva. Prisnilo sa mu, že je študentom geológie. Geológia je veda skrývajúca veľa krásy, avšak náš Mic má už odjakživa panický strach z učenia sa veľa vecí naspamäť (Všimli ste si, že slovo spam je súčasť slova naspamäť?).

V tomto nepríjemnom sne Mic práve prišiel na písomnú skúšku z minerálov. Test sa skladá z otázok, pričom každá si vyžadovala odpoveď pozostávajúcu z viacerých viet. Každá otázka je za jeden bod, ktorý skúšajúci udelí, len ak sa mu odpoveď bude zdať dostatočne vyčerpávajúca. Možno viete, že pre úspech na skúške je dôležité poradie, v akom odpovedáte na otázky. Tie sa vždy riešia celé -- nikdy nezačnete riešiť otázku, ak ste ešte neskončili s predchádzajúcou. Na niektoré otázky je lepšie odpovedať skôr, kým máte ešte v hlave text, ktorý ste si čítali tesne pred skúškou. Na niektorých otázkach je ale zase potrebné mať bystrú myseľ a dobrú koncentráciu, a tá sa zvyšuje s postupom času so vzrastajúcim adrenalínom. Na niektoré otázky je zase najlepšie odpovedať z úplne iných príčin v úplne iných fázach skúšky.

Ako vidíte, je to hotová veda. Mic si očami prebehol všetky otázky a rozmýšľa nad poradím ich zodpovedania. Pre všetky a 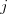medzi 1 a vrátane odhadol pravdepodobnosť, s akou zodpovie -tu otázku správne, ak ju bude riešiť ako 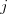-tu v poradí. Učiteľ je tvrdý a požaduje, aby študent zodpovedal všetky otázky správne. Pomôžte Micovi a zistite, s akou najväčšou pravdepodobnosťou získa plný počet bodov, ak bude otázky zodpovedať v najlepšom možnom poradí.

Úloha

Na vstupe je dané číslo -- počet otázok na skúške. Nasleduje riadkov, v každom je celých čísel. Všetky tieto čísla sú medzi 0 a 100 vrátane. Na -tom riadku 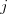-te číslo označuje pravdepodobnosť, že -ta otázka bude zodpovedaná úspešne, ak sa do nej Mic pustí ako do 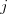-tej v poradí. Pravdepodobnosti sú v percentách.

Vypíšte jedno reálne číslo medzi 0 a 100 vrátane -- s akou najvyššou pravdepodobnosťou môže Mic zodpovedať všetky otázky úspešne, ak správne zvolí poradie ich zodpovedávania. Pre nejaké dané poradie je pravdepodobnosť plného počtu bodov rovná súčinu pravdepodobností úspešného vyriešenia pre jednotlivé otázky.

Príklad

Vstup

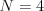
25 25 25 25
10 0 80 10
60 40 0 0
30 30 30 10

Výstup

3.6

---

Účet