- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady druhého kola letnej časti 27. ročníka KSP
Milé naše riešiteľky, milí naši riešitelia,
Termín odoslania riešení tejto druhej série je pondelok 17. mája 2010.
Najnebezpečnejší sú analfabeti, ktorí sa naučili počítať.
1. Zuckermannova torta
10 bodov, kategória Z
V cukrárenskej firme Zuckermann a syn si povedali, že na prvého apríla vydajú
špeciálnu limitovanú edíciu najpredávanejšieho tovaru -- Zuckermannovej torty.
A aby prvoaprílový duch nezostal nepovšimnutý, limitovaná edícia vznikne
z obyčajnej torty tak, že sa z jej vrchu odjedia všetky
cukríky (samozrejme, ručne. Marketingové oddelenie hneď navrhlo
pridať na krabicu nápis ručne odzdobená).
Úplnou zhodou náhod sa v tom čase ku Zuckermannovi prihlásil na brigádu Miňo,
ktorý mal neskutočnú chuť na niečo sladké. Dostal celkom jednoduchú úlohu:
v miestnosti je  stolov a na každom stole
stolov a na každom stole  tôrt s cukríkmi na vrchu. Miňo
má postupne prejsť od prvého stola k poslednému a na každom vyrobiť jednu tortu
z limitovanej edície. Vedený svojou hypoglykémiou (nízky stav cukrov
v krvi) sa rozhodol, že chce stoj čo stoj zjesť čo najviac cukríkov.
tôrt s cukríkmi na vrchu. Miňo
má postupne prejsť od prvého stola k poslednému a na každom vyrobiť jednu tortu
z limitovanej edície. Vedený svojou hypoglykémiou (nízky stav cukrov
v krvi) sa rozhodol, že chce stoj čo stoj zjesť čo najviac cukríkov.
Úloha
Na vstupe je číslo  udávajúce počet stolov v miestnosti a číslo
udávajúce počet stolov v miestnosti a číslo  udávajúce
počet tôrt na jednom stole. Nasleduje
udávajúce
počet tôrt na jednom stole. Nasleduje  riadkov s
riadkov s  číslami, ktoré postupne
hovoria o počte cukríkov na prvej, druhej,
číslami, ktoré postupne
hovoria o počte cukríkov na prvej, druhej,  ,
,  -tej torte na prvom
stole; to isté o druhom, treťom,
-tej torte na prvom
stole; to isté o druhom, treťom,  ,
,  -tom stole. Pri každom stole môže
Miňo zjesť cukríky z jednej torty, ktorá je na ňom. Vypíšte maximálny počet
cukríkov, ktoré môže Miňo zjesť.
-tom stole. Pri každom stole môže
Miňo zjesť cukríky z jednej torty, ktorá je na ňom. Vypíšte maximálny počet
cukríkov, ktoré môže Miňo zjesť.
Príklad
Vstup
3 4
4 7 4 7
1 2 8 4
3 3 3 3
Výstup
18
Vstup
5 2
1 2
2 3
3 4
4 5
5 6
Výstup
20
2. Zákerné kartičky
10 bodov, kategória Z
V predajni IBM (Institute of Black Magic) dostali novú zábavku. Ide
o Zákerné kartičky, kartovú zberateľskú hru podporujúcu myslenie (karty
IBMagic ich už omrzeli). Hra je pre dvoch hráčov a spočíva v tom, že prvý hráč
vyloží kartu a podľa nej vyloží druhý hráč svoju, ktorá musí byť rovnako veľká
(ak takú nemá, stráca náhodnú kartu). Pokiaľ prvá karta "zodpovedá" druhej,
tak obe karty dostane druhý hráč. V opačnom prípade ich dostane prvý hráč.
Karty vyzerajú ako priesvitné mriežky veľkosti 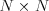 a na každom
políčku majú napísané nejaké prirodzené číslo. Dve karty si zodpovedajú,
ak vieme jednu z druhej dostať rotáciou alebo preklopením okolo vodorovnej
alebo zvislej osi (t.j. otočenie karty okolo spodnej alebo bočnej hrany).
a na každom
políčku majú napísané nejaké prirodzené číslo. Dve karty si zodpovedajú,
ak vieme jednu z druhej dostať rotáciou alebo preklopením okolo vodorovnej
alebo zvislej osi (t.j. otočenie karty okolo spodnej alebo bočnej hrany).
Takýchto kariet je samozrejme nekonečne veľa a tak nehrozí, že by niekto získal všetky a bol z toho sklamaný (na rozdiel od Pokémonov). Keď si ale IBM všimlo malú predajnosť, pochopilo, kde je problém. Porovnávanie zodpovedania kariet je pre mnohých zákazníkov problematické. Preto sa rozhodli vydať zadarmo rozšírenie obsahujúce program, ktorý pre dané dve karty povie, či si zodpovedajú.
Úloha
Na vstupe dostanete číslo  , ktoré udáva veľkosť kariet. Nasleduje
, ktoré udáva veľkosť kariet. Nasleduje  riadkov
po
riadkov
po  čísel oddelených medzerou, ktoré zodpovedajú prvej karte a potom
čísel oddelených medzerou, ktoré zodpovedajú prvej karte a potom  riadkov po
riadkov po  čísel oddelených medzerou, ktoré zodpovedajú druhej karte.
čísel oddelených medzerou, ktoré zodpovedajú druhej karte.
Na výstup vypíšte ano, ak vieme prvú kartu dostať z druhej rotáciou o 90,
180 alebo 270 stupňov, alebo preklopením okolo vodorovnej alebo zvislej osi.
Inak vypíšte nie.
Príklad
Vstup
3
1 4 0
0 1 0
2 0 1
2 0 1
0 1 4
1 0 0
Výstup
ano
Vstup
3
1 0 3
1 2 3
1 2 0
0 3 3
2 2 1
1 0 1
Výstup
nie
3. Záhada obuvníkovho sna
10 bodov, kategória Z
Kedysi, keď bola republika ešte mladá, žil jeden človek. Ten človek sa volal
Tomáš Baťa a v roku 1894 založil spolu s dvoma súrodencami a troma zamestnancami
obuvnícku firmu. V roku 1938 patrilo do jeho koncernu 63 zahraničných
spoločností, vlastná železnica do Vizovíc, cestovná kancelária, vlastná doprava,
obchodné domy... spolu vyše 67 000 zamestnancov.
Tomáš mal jeden veľký sen. Bol to skutočne sen v pravom zmysle slova, teda taký, o ktorého naplnenie sa môžete usilovať po celý život. Keďže nehrozí, že si ho úplne splníte, môžete z neho čerpať inšpiráciu až do smrti. Jeho snom bolo obuť celý svet čo najpohodlnejším spôsobom.
Detektívna kancelária Očko sa nedávno dostala na veľmi horúcu stopu a domnieva sa, že je blízko k vyriešeniu záhady okolo tragickej smrti Tomáša Baťu. Podarilo sa jej objaviť tajné databázy Baťovej firmy z čias pred vojnou, v ktorých sa nachádzajú podrobné záznamy o veľkostiach nôh takmer všetkých ľudí a tiež údaje o veľkostiach vyrobených topánok.
Ak sa zistí, že Tomáš bol blízko splnenia svojho sna, bude to vážny argument v prospech tvrdenia, že sa stal ľahkovážnym a nepozorným a práve to spôsobilo jeho smrť.
Úloha
Na vstupe dostanete dve celé čísla  a
a  , kde
, kde  je počet ľudí a
je počet ľudí a  počet
topánok v databáze. Nasleduje
počet
topánok v databáze. Nasleduje  čísel s veľkosťami nôh. Ďalší riadok obsahuje
čísel s veľkosťami nôh. Ďalší riadok obsahuje
 čísel -- veľkosti topánok.
čísel -- veľkosti topánok.
Topánka sa dá obuť iba na nohu s rovnakou alebo menšou veľkosťou. Vašou úlohou je priradiť každej nohe z databázy nejakú topánku, ktorú je na ňu možné obuť. Samozrejme, jednu topánku nemôžete priradiť na viaceré nohy. Ak existuje viac riešení, nájdite také, aby bol najväčší z rozdielov medzi veľkosťou nohy a priradenej topánky čo najmenší. Na výstup vypíšte práve tento rozdiel.
Príklad
Vstup
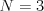
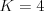
10 7 13
11 3 20 6
Výstup
nejde to
Vstup
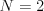
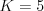
7 4
2 8 6 5 2
Výstup
1
''Nohe s veľkosťou 7 priradíme topánku s veľkosťou 8. Nohe 4 môžeme priradiť
topánku 5 alebo 6, lepšou možnosťou je 5. Takto sú obidva rozdiely medzi
veľkosťou nohy a topánky rovné 1.''
4. Zapeklitý Top Ológ
Každoročne sa na Kiribati koná súťaž o najlepšieho Ológa s názvom Top Ológ. Ako už iste tušíte, je to veľmi prestížna súťaž, v ktorej porotu tvoria zahraničné celebrity. Tento rok to budú KSPáci. Ako vyzerá takáto súťaž?
Kandidáti na najlepšieho Ológa súťažia v rôznych disciplínach, ako napríklad pľutie do výšky, hod slonom do porcelánu či surfovanie na krokodíloch. Všetky tieto disciplíny sa odohrávajú medzi dvojicami kandidátov vo veľkom Štvorcoseu za prítomnosti divákov. Keď skončia všetky súťaže, zasadne porota a zverejní výsledné poradie. KSPáci si povedali, že im sa zasadať nechce, a preto vygenerujú poradie automaticky. Aby to bolo spravodlivé, rozhodli sa, že ak Ológ A vyhral v nejakej disciplíne nad Ológom B, potom bude Ológ A vo výslednom poradí pred Ológom B. Keďže sú však KSPáci leniví, dali to vyriešiť vám.
Úloha
Prvý riadok vstupu obsahuje dve čísla  a
a  , pričom
, pričom  je počet súťažiacich
(pre jednoduchosť sú číslovaní od
je počet súťažiacich
(pre jednoduchosť sú číslovaní od  po
po  ) a
) a  je počet zápasov. Nasleduje
je počet zápasov. Nasleduje
 riadkov, každý s dvoma číslami
riadkov, každý s dvoma číslami 
 , ktoré znamenajú, že
, ktoré znamenajú, že  vyhral nad
vyhral nad
 v danom zápase. Vypíšte také výsledné poradie, v ktorom je každý súťažiaci
pred všetkými, nad ktorými vyhral aspoň v jednej súťaži (ak spolu nesúťažili,
tak na ich vzájomnom poradí nezáleží). Ak je takých poradí viac, vypíšte
ľubovoľné. V prípade, že riešenie neexistuje, podajte o tom patričnú správu.
v danom zápase. Vypíšte také výsledné poradie, v ktorom je každý súťažiaci
pred všetkými, nad ktorými vyhral aspoň v jednej súťaži (ak spolu nesúťažili,
tak na ich vzájomnom poradí nezáleží). Ak je takých poradí viac, vypíšte
ľubovoľné. V prípade, že riešenie neexistuje, podajte o tom patričnú správu.
Príklad
Vstup
5 5
1 2
3 1
2 4
3 4
5 1
Výstup
5 3 1 2 4
Vstup
5 5
1 2
3 1
2 4
4 3
5 1
Výstup
Pozadovane poradie neexistuje.
5. Ozajstná lotéria!
15 bodov, kategórie Z a O
Doteraz sme sa vás snažili nachytať rôznymi akože-lotériami. No zakaždým
sa ukázalo, že je tam nejaký háčik -- body sa neprideľovali náhodne, ale
za správne zvolený vstup.
To však už nie je pravda.
Je tu skutočná lotéria! Náhodné čísla na každom kroku! Body nezávisia len od vášho vstupu! Štyri šance vyhrať! Účinkuje aj korytnačka s dvoma hlavami! A navyše pre šťastných výhercov je tu zadarmo dvojbodová prémia navyše! Hrajte a vyhrajte!
Lotéria sa dá hrať jedine online, a to na adrese http://old.ksp.sk/loteria/.
Tam tiež nájdete program, ktorý bude vašim riešeniam prideľovať body.
Hrať lotériu môžete ľubovoľne veľa krát. Ale pozor!
Hodnotiť sa bude len váš posledný pokus. A navyše len prvých 5 pokusov
je zadarmo -- ak dokopy spravíte 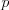 pokusov, od vášho výsledného
bodového zisku odrátame dolnú celú časť z
pokusov, od vášho výsledného
bodového zisku odrátame dolnú celú časť z 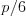 bodov (nebojte sa,
pod nulu sa klesnúť nedá :-)).
bodov (nebojte sa,
pod nulu sa klesnúť nedá :-)).
6. Orientálny trh
20 bodov, kategória O
Šejk hadži Halef Omar ben hadži Abú'l Abbás ibn hadži Dávúd al Gossarah (ďalej
len Halef, snáď nám to prepáči) má za manželku Hanneh, tú najmúdrejšiu,
najkrajšiu a najlepšiu ženu na svete. Ale až po svadbe objavil jej ďalšiu
vlastnosť: Hanneh má vždy pravdu a preto ju treba vo všetkom poslúchať.
Napríklad teraz si uvedomila, že ostatní šejkovia vlastnia obrovské háremy a ona
si tu nemá s kým vymieňať špekulácie o ďalšom deji jej obľúbenej nemeckej
telenovely Sila lásky. Preto prikáz... éé... požiadala Halefa, aby šiel na
trh a kúpil tam  dám do ich novozaloženého háremu.
dám do ich novozaloženého háremu.
Na trhu predávajú háremové dámy iba v jedinej ulici. Tá má na ľavej strane  stánkov s dámami a oproti každému je na pravej strane ulice stánok s bižutériou,
zlatníctvo alebo predajňa obuvi. Halef chce prejsť ulicou len raz, v smere od
prvého stánku ku
stánkov s dámami a oproti každému je na pravej strane ulice stánok s bižutériou,
zlatníctvo alebo predajňa obuvi. Halef chce prejsť ulicou len raz, v smere od
prvého stánku ku  -temu. Má to ale háčik. Dámy, ktoré už kúpil, vyžadujú, aby
sa zastavili v každom stánku na pravej strane, okolo ktorého ešte pôjdu. A keby
len zastavili...
-temu. Má to ale háčik. Dámy, ktoré už kúpil, vyžadujú, aby
sa zastavili v každom stánku na pravej strane, okolo ktorého ešte pôjdu. A keby
len zastavili...
Halef sa už zmieril s tým, že mu bude nákup trvať celý deň. Pomôžte mu ho naplánovať tak, aby pri ňom minul čo najmenej peňazí.
Úloha
Na vstupe dostanete v prvom riadku čísla  a
a  . Druhý a tretí riadok budú
obsahovať čísla
. Druhý a tretí riadok budú
obsahovať čísla  a
a  -- cenu za dámu a počet
dám, ktoré majú na sklade v jednotlivých stánkoch na ľavej strane ulice.
V štvrtom riadku budú čísla
-- cenu za dámu a počet
dám, ktoré majú na sklade v jednotlivých stánkoch na ľavej strane ulice.
V štvrtom riadku budú čísla  -- suma, ktorú nechá každá dáma
v jednotlivých stánkoch na pravej strane ulice.
-- suma, ktorú nechá každá dáma
v jednotlivých stánkoch na pravej strane ulice.
Dáma kúpená v  -tom obchode teda stojí Halefa
-tom obchode teda stojí Halefa
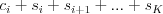 peňazí. Samozrejme, Halef nemôže v žiadnom stánku kúpiť viac dám, ako majú
na sklade. Vašou úlohou je vypísať najmenšiu sumu, ktorá stačí na kúpu
peňazí. Samozrejme, Halef nemôže v žiadnom stánku kúpiť viac dám, ako majú
na sklade. Vašou úlohou je vypísať najmenšiu sumu, ktorá stačí na kúpu  dám
do háremu. Môžete predpokladať, že riešenie vždy existuje
(
dám
do háremu. Môžete predpokladať, že riešenie vždy existuje
(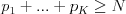 ).
).
Príklad
Vstup
1 3
3 6 1
7 2 0
4 4 4
Výstup
14
''Halef môže kúpiť dámu iba v prvom alebo druhom stánku. Oplatí sa mu druhý
stánok, zaplatí tak 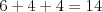 namiesto
namiesto 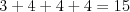 .''
.''
Vstup
3 4
5 6 7 15
1 1 1 1
2 3 2 8
Výstup
56
7. Oranžové stužky
20 bodov, kategória O
Každoročne sa koná medzi dedinkami Nikde a Niekde turnaj v hre Oranžové stužky.
Nie, nie je to počítačová hra, aj keď v posledných rokoch sa premnožili úspešné
pokusy o využitie počítačov aj pri tejto detskej hre.
Pôvodnú detskú hru hralo ľubovoľne veľa dievčat a chlapcov, ak mali dosť stužiek. Stužky hodili na zem a postavili sa do kruhu okolo nich. Každý náhodne chytil dáke konce stužiek a zdvihol ich do vzduchu (nikdy sa nestalo a nestane, že by chytil oba konce tej istej stužky). Tak boli deti zrazu pospájané. Pointou hry bolo vyhodiť niektoré stužky z kruhu (vyhodenú stužku obe deti pustia z ruky) tak, aby všetkým dievčatám ostal v rukách párny počet stužiek a chlapcom nepárny. Stužky môžu len vyhadzovať, nesmú si ich medzi sebou vymieňať.
Súťažná verzia sa líši len v pár drobnostiach: na začiatku hry zvolí rozhodca náhodný počet dievčat a chlapcov pre tohoročnú súťaž a obe dediny postavia svoje tímy. Potom oba tímy pospája stužkami rozhodca podľa plánu, ktorý si vytvoril. A spustí sa časomiera.
Vyhrá tím, ktorý ako prvý dosiahne párny počet stužiek u dievčat a nepárny u chlapcov. Ak to nie je možné, vyhrá ten, kto prvý vykríkne, že sa to nedá (ale hanba za nesprávny výkrik je veľká, a tak nikto neriskuje, kým si nie je istý).
Šikovní žiaci z Niekde si povedali, že využijú počítače. Preto sa obrátili na vás, aby ste im pomohli a čo najrýchlejšie našli riešenie na zadanie, ktoré dostanú na súťaži.
Úloha
Na vstupe dostanete počet detí  a počet stužiek
a počet stužiek  . Nasleduje
. Nasleduje  riadkov,
ktoré popisujú jednotlivé stužky. Každý z nich je v tvare
riadkov,
ktoré popisujú jednotlivé stužky. Každý z nich je v tvare 
 -- čísla detí,
ktoré držia danú stužku. Posledný riadok obsahuje reťazec
-- čísla detí,
ktoré držia danú stužku. Posledný riadok obsahuje reťazec  znakov
znakov D
(dievča) a C (chlapec) popisujúci pohlavie jednotlivých detí.
Ak existuje riešenie, vypíšte čísla stužiek, ktoré majú zostať v kruhu, aby boli
splnené podmienky hry. V opačnom prípade vypíšte nemozne.
Príklad
Vstup
4 4
1 2
2 3
3 4
4 1
CDCD
Výstup
1 2
''Deti 1 a 3 budú držať po jednej stužke, dieťa 2 bude držať 2 stužky a dieťa
4 ani jednu.''
Vstup
3 2
1 2
1 2
DDC
Výstup
nemozne
8. Temné častice
25 bodov, kategórie O a T
V IBM sa rozhodli vyskúšať novú metódu ťažby temných častíc.
Na čo sa takéto častice používajú? To je prísne tajné.
Odkiaľ sa berú? Temná častica vznikne, keď sa zrazia dve neutréna (také trochu ťažšie a trochu pomalšie letiace neutríno) (tieto neutréna po zrážke letia presne rovnako, ako leteli predtým). A v tom je práve problém. Zachytiť neutréna je veľký problém.
Inžinierom z IBM sa podarilo zachytiť niektoré dráhy neutrén. Teraz už len pripraviť lapač temných častíc. Problém je, že lapače sú iba obdĺžnikové a musia byť umiestnené tak, aby ich strany boli rovnobežné so súradnicovými osami. Keďže je kríza, v IBM nemajú veľa peňazí, takže chcú kúpiť čo najmenší lapač, ale zároveň chcú pochytať všetky temné častice.
Zaregistrovali sme, že sa na nástenke v IBM objavil tender o najlepší program, čo bude riešiť tento problém. Zapojíte sa?
Úloha
Daných je  priamok. Vašou úlohou je vypísať také čísla
priamok. Vašou úlohou je vypísať také čísla 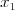 ,
, 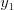 ,
, 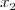 ,
,
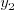 , že všetky priesečníky priamok sa nachádzajú vo vnútri (alebo na okraji)
obdĺžnika s vrcholmi
, že všetky priesečníky priamok sa nachádzajú vo vnútri (alebo na okraji)
obdĺžnika s vrcholmi 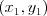 ,
, 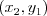 ,
, 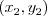 ,
, 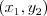 a zároveň rozmery tohto obdĺžnika sú najmenšie možné.
a zároveň rozmery tohto obdĺžnika sú najmenšie možné.
Na vstupe je najprv číslo  . Nasledujú popisy
. Nasledujú popisy  priamok, pričom priamka je
daná číslami
priamok, pričom priamka je
daná číslami 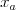 ,
, 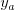 ,
, 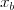 ,
, 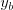 . Tieto čísla určujú dva rôzne body
. Tieto čísla určujú dva rôzne body
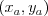 a
a 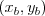 , cez ktoré priamka prechádza. Môžete predpokladať,
že
, cez ktoré priamka prechádza. Môžete predpokladať,
že  a žiadne dve zo zadaných priamok nie sú rovnobežné.
a žiadne dve zo zadaných priamok nie sú rovnobežné.
Príklad
Vstup
3
-1 0 1 0
0 -1 0 1
2 -1 -1 2
Výstup
0 0 1 1
9. Tancujúce víly
25 bodov, kategória T
Pri splne tancujú,
kvetinky milujú,
naše malé víly,
čo Usámu zbili.
Potom, čo Víla Amálka vyhrala na AnimeShow v DDR hard turnaji 3. miesto a skoro pritom vypľula svoju dušu, rozhodla sa, že načas opustí túto brandžu a pustí sa radšej do jemnejších športov.
Je to už raz tak, jemné víly nemajú veľa síl, aby skákali tak rýchlo. Ako každá správna víla ale nechce prestať tancovať. Preto sa pridala k známej skupine Veela Moon Dance. Isto to poznáte: čistinka uprostred lesa, kde nikto nie je, iba nádherná lúka s kvetmi a pri splne mesiaca tancujúce víly vo svojich jemných priesvitných šatách. Nuže i zverila sa Víla Amálka svojmu kamarátovi Usámcovi (čítaj uSAMEC), že dáva na chvíľu zbohom Stepmánii a ide po mesačných nociach flámovať na lúky.
Hneď, ako Usámec počul, čo za šport sa to rozhodla pestovať, zablysli sa mu očičká (alebo skôr očúle). (Každý asi tuší, že záhadný lesk v očiach asi nie je kvôli tancu pri mesačnom splne, ale skôr kvôli tým jemným priesvitným šatám.) Hneď sa začal o tanec zaujímať (a tajne plánovať, ako sa pri najbližšom splne nepozorovane dostane na tú čistinku).
Amálka sa záujmu o jej nový tanec potešila a vysvetlila aj jeho choreografické prvky. Vílí tanec je pomerne jednoduchý. Na začiatku sa všetky víly rozmiestnia do niekoľkých kruhov po celej čistinke. V okamihu, keď trikrát zahúka sova a cvrčky začnú svoj trilkot, víly sa roztancujú.
Každý kruh sa začne točiť do jednej strany. Samozrejme, víly sa pritom
otáčajú (drvivú väčšinu času podľa osi  ), jemne poskakujú, dávajú
pozor, aby náhodou nestúpili na nejaký kvietok, spievajú mesačné árie, ktoré by
zmedovateli i toho najväčšieho drsňáka a ešte mnohé iné činnosti.
), jemne poskakujú, dávajú
pozor, aby náhodou nestúpili na nejaký kvietok, spievajú mesačné árie, ktoré by
zmedovateli i toho najväčšieho drsňáka a ešte mnohé iné činnosti.
Ako každý správny vílí tanec, i tento je perfektne synchronizovaný a je radosť naň pozerať. Tancovanie víl dokola vo svojich kruhoch sa opakuje až do momentu, keď sa všetky víly dostanú naraz na svoje pôvodné miesta. Vtedy sa tanec končí.
Nuže v tomto uvidel Usámec svoju šancu -- pretože od toho, ako sa víly na začiatku rozostavia, závisí dĺžka trvania tanca, stačí nájsť vhodné rozostavenie tak, aby bol tanec zaujímavý (rozumej čo najdlhší). Usámec preto presvedčil Vílu Amálku, že jej povie, ako sa majú víly na začiatku rozmiestniť, aby bol tanec čo najkrajší, s čím Amálka ihneď súhlasila. Teraz ale ostáva Usámcovi jedna ťažká úloha -- aké je vlastne to rozloženie?
Úloha
Na vstupe je dané jediné číslo  -- počet víl, ktoré budú tancovať počas
najbližšieho splnu. Vašou úlohou je vypísať permutáciu najväčšieho rádu,
t.j. permutáciu takú, že počet jej opakovaných aplikovaní na dosiahnutie
počiatočnej permutácie je najväčší možný.
-- počet víl, ktoré budú tancovať počas
najbližšieho splnu. Vašou úlohou je vypísať permutáciu najväčšieho rádu,
t.j. permutáciu takú, že počet jej opakovaných aplikovaní na dosiahnutie
počiatočnej permutácie je najväčší možný.
Poznámka, hint a iné:
Permutácia je vlastne preusporiadanie. Presnejšie, ak si pod ňou
predstavíme postupnosť 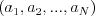 , tak číslo
, tak číslo 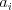 nám hovorí,
kam poslať vílu, ktorá teraz stojí na pozícii
nám hovorí,
kam poslať vílu, ktorá teraz stojí na pozícii  . Samozrejme požadujeme,
aby všetky tieto čísla boli z rozsahu
. Samozrejme požadujeme,
aby všetky tieto čísla boli z rozsahu 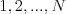 a navzájom rôzne.
Takéto preusporiadanie môžeme aplikovať viackrát po sebe.
a navzájom rôzne.
Takéto preusporiadanie môžeme aplikovať viackrát po sebe.
Keď si teraz zoberieme vílu na pozícii  a niekoľkokrát aplikujeme permutáciu,
tak táto víla skončí časom opäť na pozícii
a niekoľkokrát aplikujeme permutáciu,
tak táto víla skončí časom opäť na pozícii  . Vezmime si pozície, ktorými
prešla. Môžeme si všimnúť, že víly z týchto pozícií sa nikdy nedostanú mimo
nich. Takto môžeme permutáciu rozbiť na cykly (kruhy).
. Vezmime si pozície, ktorými
prešla. Môžeme si všimnúť, že víly z týchto pozícií sa nikdy nedostanú mimo
nich. Takto môžeme permutáciu rozbiť na cykly (kruhy).
Príklad
Vstup
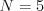
Výstup
2 3 1 5 4
Víly sa rozmiestnia do 2 kruhov:
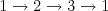 a
a 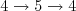 , prvý kruh sa otočí po 3 krokoch, druhý kruh sa otočí po 2 krokoch, a teda všetky víly sa budú nachádzať opäť na svojom počiatočnom mieste po 6 krokoch.
, prvý kruh sa otočí po 3 krokoch, druhý kruh sa otočí po 2 krokoch, a teda všetky víly sa budú nachádzať opäť na svojom počiatočnom mieste po 6 krokoch.
10. Teroristické bunky
25 bodov, kategória T
Ako ste už počuli v správach, na svete sú zlí ľudia nazývaní teroristi. Tí sa
delia do takzvaných buniek, z ktorých niektoré sú spolu v kontakte a vymieňajú
si aktívne informácie. Tie odpočúva Komisia na Sledovanie Prenosov (KSP), ktorá
potom zisťuje, koho treba ratovať a koho zatýkať. Lenže také odpočúvanie sa vie
aj nevydariť.
Agentovi KSP Plžíkovi sa podarilo z teroristických kuloárov zistiť, že bunky 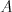 a
a 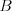 chystajú niečo ozaj veľké (a KSP by to samozrejme zaujímalo)!
Tieto dve bunky nie sú v kontakte priamo. A to je šanca, ktorú treba využiť. KSP
dostalo povolenie zlikvidovať niekoľko buniek tak, aby každá komunikácia medzi
chystajú niečo ozaj veľké (a KSP by to samozrejme zaujímalo)!
Tieto dve bunky nie sú v kontakte priamo. A to je šanca, ktorú treba využiť. KSP
dostalo povolenie zlikvidovať niekoľko buniek tak, aby každá komunikácia medzi
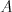 a
a 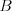 musela prejsť aspoň cez dve ďalšie bunky (aby sa dala po ceste
kvalitne odpočuť).
musela prejsť aspoň cez dve ďalšie bunky (aby sa dala po ceste
kvalitne odpočuť).
Keďže je munícia drahá, chcú samozrejme v KSP minimalizovať počet likvidácií. Preto sa obrátili na vás, aby ste napísali program na určenie, ktoré bunky treba zničiť.
Úloha
Na vstupe je popis grafu 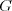 a zadané dva vrcholy
a zadané dva vrcholy 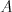 a
a 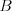 , medzi ktorými
nevedie hrana. Vašou úlohou je odstrániť z
, medzi ktorými
nevedie hrana. Vašou úlohou je odstrániť z 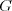 čo najmenej vrcholov (rôznych od
čo najmenej vrcholov (rôznych od
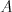 a
a 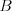 ) tak, aby medzi vrcholmi
) tak, aby medzi vrcholmi 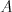 a
a 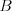 neexistovala cesta prechádzajúca
cez menej ako
neexistovala cesta prechádzajúca
cez menej ako 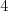 hrany.
hrany.
Vypíšte čísla odstránených vrcholov.
Príklad
Vstup
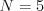
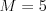
1 2
1 3
2 4
3 4
4 5
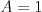
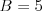
Výstup
4
Posledná úprava 31 marec, 2010, 20:37 CET, túto podstránku generuje pmWiki

