Korešpondenčný seminár z programovania

1. Zbláznil sa fyzikár...

10 bodov, kategória Z
Váš učiteľ fyziky sa rozhodol vyskúšať nové pedagogické metódy. Už sa na hodinách skoro nič neučíte, len stále experimentujete a niečo meriate. To mu nemožno až tak zazlievať, aspoň vidíte fyzikálne deje v praxi. No napriek tomu všetci spolužiaci frflú, že sa azda pomiatol, veď zadáva jednu domácu úlohu za druhou.

Posledný mesiac ste strávili neustálym spisovaním protokolov z laboratórnych cvičení. Bolo toho tak veľa, že sa to jednoducho nedalo stíhať -- mnoho z nich ste dopisovali narýchlo, tesne pred hodinou. A tak nečudo, že fyzikár nebol s kvalitou spokojný. Údaje nepresné, výpočty chýbajú, tabuľky len krivo rukou načmárané, namiesto aby boli poriadne narysované.

Verdikt: prepracovať! No ešte to tak chýbalo! Čo teraz? Nechce sa vám predsa všetko robiť odznova. Fajn, obsah môžete odpísať od svedomitejších spolužiakov, ale tie tabuľky... tie bude treba narysovať, jednu za druhou. Desiatky tabuliek... nezáživná, zdĺhavá, mechanická práca... priam práca pre robota, nie človeka. Teda, robota alebo... počítač! Pri tejto spásonosnej myšlienke sa vám uľavilo. Ešteže viete programovať!

Úloha

Napíšte program, ktorý na vstupe dostane dve prirodzené čísl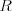a a 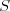a vykreslí tabuľku s 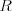riadkami a 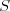stĺpcami. Na vodorovné línie použite znak '-' (mínus, resp. pomlčka), na zvislé línie znak '|' (tzv. rúra) a na ich priesečníky znak '+' (plus). Každé políčko tabuľky je tvorené jedinou medzerou tesne ohraničenou vertikálnymi a horizontálnymi líniami.

Príklad

Vstup

2 3

Výstup

+-+-+-+
| | | |
+-+-+-+
| | | |
+-+-+-+

---

2. Zrkadielko, zrkadielko, povedz že mi...

10 bodov, kategória Z
A je to tu zas. Snehulienkina macocha sa opäť raz pozerá do zrkadla. To síce touto skvostnou panorámou nie je nadšené, nuž ale čo má robiť. Ako má odpovedať? Odpovie, že nie je najkrajšia a... budú z neho tisíce zrkadiel. V rámci záchrany svojho života sa zrkadlo pokúsilo o lacný trik:

"Zrkadielko, zrkadielko, povedz že mi, kto je najkrajší v tejto zemi?"

"Ty, kráľovná. Ale bola by si ešte krajšia, ak by si mala unikátny náhrdelník."

Kráľovná sa teda rozhodla, že si zabezpečí unikátny náhrdelník. To však nie je také jednoduché. Swarovski majú len malý výber a žien v kráľovstve je veľa. Tadiaľ teda cesta nevedie. A žiadať kráľa o nový náhrdelník je asi ako žiadať žabu o princa.

Po dlhom hneve, počas ktorého zrkadlo skoro stratilo svoju tvár (resp. presnejšie povedané, skoro nové tváre získalo), zrkadlo uznalo, že to možno trochu prehnalo. Preto svoj výrok upravilo tak, že stačí, aby bol náhrdelník inak pootočený.

Kráľovná si je teraz istá, že bude najkrajšia na zemi. Potrebovala by však overiť, či je dané otočenie náhrdelníka naozaj unikátne. A na to ho musí najprv vidieť.

Úloha

Na prvom riadku vstupu je reťazec znakov (anglickej abecedy), popisujúci náhrdelník. Na druhom riadku vstupu je jedno celé číslo hovoriace, o koľko treba náhrdelník pootočiť (smerom "doľava"). Náhrdelník sa môže iba otáčať, nemôže sa preklápať (inak by bolo vidno na niektorých šperkoch "made in China" a to, samozrejme, nechceme).

Na výstup vypíšte jeden riadok -- pootočený náhrdelník.

Obmedzenia:

Pri tejto úlohe kladieme ešte nasledujúce obmedzenia: váš program si má daný náhrdelník pamätať v jednej premennej typu reťazec, ktorej obsah môže meniť. Nesmiete však používať ďalšie pomocné reťazce ani polia (Obyčajných premenných môžete použiť, koľko sa vám zažiada.). Na výstup vypíšte obsah premennej typu reťazec, do ktorej ste na začiatku načítali náhrdelník zo vstupu (vypíšte ho jediným príkazom, nie po znakoch).

Ak tieto obmedzenia nedodržíte, hrozí vám strata väčšieho počtu bodov...

Kostra riešenia v Pascale:

Príklad

Vstup

totojenahrdelnik
4

Výstup

jenahrdelniktoto

---

3. Zase ďalšia Alica?

10 bodov, kategória Z
Alica žila v ríši divov. No dobre, nie tak celkom divov, ale divné to tam bolo až-až. Ani Srdcová kráľovná nebola, čo bývala v rozprávkach. Vlastne, hovorilo sa, že je dosť schopná matematička. Ale stínanie hláv mala rada presne rovnako, ako sa povrávalo v príbehoch pre deti.

Po tom, čo chytila Alicu, sa rozhodla, že si s ňou namiesto kriketu zahrá svoju obľúbenú hru. Vygenerovala dve náhodné čísla a ku každému náhodný počet výkričníkov (V skutočnosti jej generátor robili Tidli a Fidli, ktori mali po sebe napísané čísla a následne tancovali breakdance.). Potom tieto čísla dala svojmu súperovi a ten musel rýchlo povedať, ktoré je väčšie. Počet výkričníkov vyjadruje koľko krát sme použili faktoriál. Napríklad platí 3!! = 6! = 720. A kto neuhádol, tomu dala sťať hlavu.

Alica sa preto rozhodla, že vás požiada o pomoc, aby ste jej naprogramovali program, ktorý jej odpoveď povie sám.

Úloha

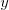Na vstupe máte zadané dva riadky. V prvom riadku je číslo a za ním (po medzere) nejaký počet výkričníkov, v druhom riadku je číslo a za ním (po medzere) nejaký počet výkričníkov. Máte určiť, ktorý z riadkov zodpovedá väčšiemu číslu a vypísať ho. Ak sú obe čísla rovnaké, vypíšte "rovnake". Môžete predpokladať, že .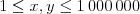

Príklad

Vstup

3 !! 7 !

Výstup

7 !

---

4. Zabité dekódovanie

15 bodov, kategórie Z a O
Vesmírna loď Enterprise po dlhej bitke s Borgskou kockou utrpela ťažké poškodenie. Okrem toho, že jej vypadol warpový pohon, tak prestali fungovať aj dekodéry galaktických prenosov. A to je vcelku problém, keďže nemôžu prijímať rozkazy od armádneho velenia (A za ich nerešpektovanie kapitán Picard dostane železnou tyčou.). Preto treba nakódiť nový dekóder.

Galaktické prenosy sú kódované nasledovne. Prenášaný text sa rozseká na slová. Každé slovo má jednoznačne priradený kód (postupnosť a ). Navyše tieto kódy sú priradené tak, aby žiadny z nich nebol prefixom (predponou, napr. 011 je prefixom 01100) iného (Toto zaručuje niekoľko príjemných vlastností, napríklad jednoznačné dekódovanie.). A potom sa kódy v jednej súvislej postupnosti prenesú.

Úloha

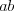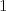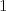Na vstupe je číslo -- počet kódových slov. Nasleduje riadkov tvaru , kde je nejaké slovo pozostávajúce z písmen malej anglickej abecedy a je jeho zakódovaný tvar -- reťazec z a . Môžete predpokladať, že žiadny zakódovaný tvar nie je prefixom iného zakódovaného tvaru. Potom nasleduje číslo -- dĺžka zakódovanej postupnosti a za tým samotná postupnosť z a . Vašou úlohou je túto postupnosť dekódovať, teda vypísať na výstup pôvodné slová oddelené medzerou. Môžete predpokladať, že postupnosť sa vždy dá dekódovať.

Môžete predpokladať, že 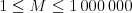, 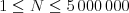a že dĺžky slov sú men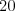šie ako , dĺžky kódov sú menšie ako 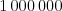a celkový súčet dĺžok kódov je menší ako .

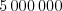Odovzdávanie:

Tento príklad je praktický, čo znamená, že sa dá odovzdáva jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v časovom limite.

Poznamka o vystupe

Slová majú byť oddelené práve jednou medzerou (nie novým riadkom). Za posledným slovom nemá byť žiadna medzera, iba znak nového riadku.

Príklad

Vstup

3
slama 111
seno 010
ryba 0111
13
1110100100111

Výstup

slama seno seno ryba

---

5. Otrávený duel

15 bodov, kategórie Z a O
Lord Norton a lord Berkley sa pohádali priam až do krvi a rozhodli sa, že si dajú spravodlivý duel. Lord Norton má však tenisový lakeť v kolene a preto duel nemôže byť v žiadnej fyzickej disciplíne. Preto si vybrali smrteľnú mentálnu disciplínu. Zohnali si špeciálny jed. Pri bežnom jede zomrie ten, kto ten jed vypije. Ale pri tomto jede zomrie ten, čo vypije posledný dúšok.

Ako sa hrá tento smrteľný duel? Zoberie sa jed a rozdelí sa do pohárov. Týchto pohárov sa rozdelí do kruhov. V každom ťahu si jeden z lordov vyberie 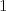až 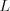pohárov jedu (nie nutne z toho istého kruhu), vypije ich a kruhy, z ktorých vybral nejaké poháre, spojí do jedného veľkého kruhu. Lordi sa striedajú a nečakane, kto vypije posledný pohár, ten prehral (a zomrel).

KáeSPáci by radi vedeli, kto vyhrá, ale sú strašné lamy a nevedia si to zistiť. Preto im pomôžte a spravte program, ktorý zistí výsledok.

Úloha

Vašou úlohou je pre dané , , 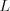a veľkosti jednotlivých kruhov povedať, ktorý lord vyhrá, ak začína lord Norton a obaja lordi hrajú optimálne.

Príklad

Vstup

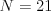
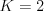
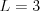
9 12

Výstup

Vyhrá lord Berkley

---

6. Oliaty koberec

20 bodov, kategória O
Mali sme raz na T2 modrý koberec. Teraz síce máme stále ten istý koberec, ale už nie je len modrý. Sem-tam sa stane, že ho niekto niečím oleje. A keďže náš koberec nie je najmladší, zažil už niekoľko generácií. A každá z týchto generácií na ňom zanechala nejaké stopy v podobe rôznych fľakov.

Halucinka má však rada poriadok, a tak sa rozhodla, že ho trochu vyčistí. Akurát nemala čím. Našťastie v matfyzáckom bufete majú aj čistiace prostriedky. A nie hocijaké. Jeden čistiaci prostriedok vyčistí ľubovoľne veľký fľak. A aby toho nebolo málo, v bufete majú aj špiniace prostriedky. Tie fungujú podobne ako čistiace, akurát opačne -- zašpinia ľubovoľne veľkú čistú plochu. Jediným problémom je, že sú veľmi drahé (oba rovnako) a treba nimi šetriť. Pomôžte Halucinke vymyslieť, ako vyčistiť koberec tak, aby minula čo najmenej čistiacich a špiniacich prostriedkov.

Úloha

Prvý riadok vstupu obsahuje dve čísla -- 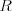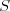-- rozmery koberca. Za tým nasleduje 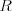riadkov dlhých 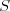, ktoré popisujú koberec. Bodka ('.') znamená čisté miesto a hviezdička ('*') znamená špinavé miesto. Okraj koberca bude zaručene čistý.

Dve susedné špinavé políčka patria do toho istého fľaku práve vtedy, keď susedia stranou (iba rohom nestačí). Dve susedné čisté políčka patria do tej istej čistej plochy práve vtedy, keď susedia stranou alebo rohom.

Fľak môže obklopovať čistú plochu, ktorá môže obklopovať ďalšie fľaky, atď. Žiadny fľak ale nebude (priamo) obklopovať viac ako jednu súvislú čistú plochu. Z nasledujúcich situácií je teda prvá povolená, ale druhá nie:

***** *****
*...* *.*.*
*.*.* *.*.*
*...* *.*.*
***** *****

Napíšte program, ktorý zistí, koľko najmenej čistiacich a špiniacich prostriedkov dokopy treba na vyčistenie koberca.

Príklad

Vstup

5 11
...........
....**.***.
...*...*.*.
.***...***.
...........

Výstup

2

Na koberci sú tri fľaky. Zašpiníme ľavý horný roh koberca, takže bude celý špinavý okrem jediného štvorčeka. Potom ho naraz vyčistíme.

---

7. Odhaľ komunikačnú sieť!

20 bodov, kategória O
Tvoja krajina je vo vojne! Má však špióna u nepriateľa. Veliteľstvo by rado zistilo, ako vyzerá komunikačná sieť nepriateľa. Už vie počet a zoznam komunikačných zložiek nepriateľa. Vie dokonca aj to, že komunikácia medzi jednotlivými zložkami prebieha po grafe typu strom (tzn. neobsahuje cykly). 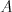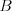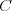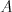Problémom je, že dohodnutá komunikácia s vašim špiónom je obmedzená nasledovne: špióna sa môžete spýtať len to, či sa a dohovárajú prostredníctvom a on vám odpovie áno, ak správy medzi a 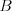prechádzajú v nepriateľovej sieti cez .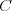

Úloha

Na vstupe je počet komunikačných zložiek nepriateľa . Vašou úlohou je spraviť algoritmus, ktorý bude postupne klásť otázky typu 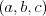, kde , , sú čísla zložiek nepriateľa (, , 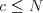). Na základe odpovedí vypíšte zoznam dvojíc, ktoré komunikujú priamo (tzn. nie cez prostredníka). Odpoveď áno dostanete vtedy, ak , komunikujú cez , inak dostanete odpoveď nie (uvedomte si, že stále môžu komunikovať aj cez inú zložku ).

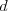Príklad

Vstup

nie
ano

Výstup

1 2 3
1 3 2

1 2
2 3

---

8. O dračej invázii

25 bodov, kategória O
Kde bolo, tam bolo, bolo raz jedno kráľovstvo. V tom kráľovstve bol hrad a mestá pospájané obojsmernými cestami tak, že sa dalo z každého mesta dostať do hradu.

Jedného dňa však priletelo zopár drakov. Každý si vybral nejaké mesto (nie hrad), ktoré spustošil, zožral jeho obyvateľov, usadil sa v ňom a začal zle vplývať na cestovný ruch -- cez mesto obsadené drakom totiž nikto živý neprejde.

V niektorých mestách sídlili zemepáni. A práve od nich sa kráľ dozvedel o invázii drakov. Presnejšie, ak sa živý zemepán (to znamená, že ho nezožral drak!) nemohol zo svojho mesta dostať do hradu, poslal kráľovi holubou poštou list. V ňom sa sťažoval na drakov, farbisto opísal svoju situáciu (Óch, ja nešťastný zemepán) a žiadal okamžitú nápravu. Žiaľ, zabudol spomenúť, v ktorýchže to mestách vlastne videl drakov.

Pomôžte zhrozenému kráľovi zistiť, aké škody sú spôsobené v tom najlepšom možnom prípade. Najmenej z koľkých miest sa nedá dostať do hradu (vrátane tých obsadených drakmi)?

Úloha

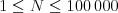Na vstupe dostanete v prvom riadku čísla (počet miest, ), (počet ciest, 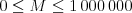) a 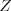(počet správ od zemepánov, 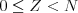) oddelené medzerami.

Mestá kráľovstva sú očíslované od 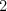do , hrad má číslo 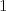. Nasleduje riadkov v tvare , ktoré popisujú cestnú sieť -- obojsmerná cesta spája miesta a ().

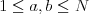Na poslednom riadku je 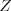čísel oddelených medzerami -- mestá, z ktorých sa ozvali zemepáni. Tieto mestá neboli obsadené drakmi, len sa z nich nedá dostať po cestách do hradu bez navštívenia mesta s drakom.

Vypíšte najmenšie také číslo , že existuje rozmiestnenie drakov, ktoré spĺňa podmienky zo vstupu (teda že nešťastní zemepáni sa nemôžu dostať do hradu) a počet miest, z ktorých sa nedá dostať do hradu, je práve .

Odovzdávanie:

Tento príklad je praktický, čo znamená, že sa dá odovzdáva jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v časovom limite.

Príklad

Vstup

5 5 1
1 2
1 3
2 3
2 4
4 5
4

Výstup

3

Mesto 2 je určite obsadené drakom; z miest 4 a 5 sa určite nedá dostať do hradu.

---

9. Tvoriví mládenci

25 bodov, kategória T
Starí mládenci Bob a Nishrep nie sú takí priemerní ako väčšina mužov v ich veku. Zatiaľ čo ostatní majú štandardné záujmy ako manželky, futbal alebo autá, Boba a Nishrepa spája veľká spoločná vášeň -- pestovanie rastlín. Každý z mládencov má pred svojím domom dlhý chodník, vedľa ktorého sa tiahne prekrásny rad pestrofarebných kvetov. Táto harmónia farieb a vôní je výsledkom dlhoročnej práce a zodpovedného prístupu.

Bob má vo svojom rade 26 typov kvetov, ktoré si ako správny vyštudovaný programátor označuje malými písmenami anglickej abecedy. Preto si jeho rad môžeme reprezentovať ako reťazec písmen. Zatiaľ čo ľubovoľná nematfyzácka dôchodkyňa by svoje štyri kvety v rade vymenovala slovne (levanduľa, astra, margarétka a znova astra), Bob svoju záhradku označuje skrátene lama.

Jedného dňa sa Bob rozhodol, že skúsi Nishrepovi povedať presný popis jeho radu kvetov. Ten je ale natoľko dlhý, že starému pestovateľovi robí ťažkosti zapamätanie si už aj jeho písmenkového označenia. Preto sa rozhodol, že si zapamätá len nejakú skomprimovanú verziu, ktorá mu bude stačiť na to, aby u Nishrepa zrekonštruoval celý svoj pás kvetov. Vymyslel si nasledovný, ľahko zapamätateľný, postup: ak X je ľubovoľný neprázdny reťazec znakov, tak ak sa v slove za sebou vyskytuje 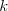-krát reťazec X, potom si namiesto XXX stačí zapamätať k[X]. Samozrejme, toto môžeme robiť aj rekurzívne. Napríklad reťazec aaabaaabaaab môžeme zakódovať ako 3[a]b3[a]b3[a]b, čím sme dĺžku kódu síce zväčšili, ale môžeme pokračovať ďalej a tento reťazec zakódovať ako 3[3[a]b] a dostať kód dĺžky 8 (oproti pôvodným 12). Avšak, ak by sme pôvodný reťazec radšej zakódovali ako 3[aaab], dostávame dokonca dĺžku 7. Samozrejme, že číslo môže mať aj dlhší dekadický zápis ako jeden znak.

Úloha

Vašou úlohou je pre pôvodný reťazec Bobovej záhrady získať najkratší možný kód v popísanom kódovaní. Inými slovami, vypíšte reťazec pozostávajúci z malých písmen anglickej abecedy, cifier a hranatých zátvoriek, ktorý sa dekóduje na vstupné slovo a spomedzi všetkých takýchto kódov nájdite najmenší. V prípade viacerých možností vypíšte ľubovoľnú.

Príklad

Vstup

abcabcbcbc

Výstup

abca3[bc]

Ďalší zaujímavý spôsob zakódovania by bol 2[abc]2[bc], avšak ten je o dva znaky dlhší.

---

10. Teória výberu suseda

25 bodov, kategória T
Prišiel raz MišoF v polke veľkého stretka do KSPárne a pozerá na diskutujúcich ľudí. Žiadny KSPák sa na veľkom stretku okrem mentálnych kvalít nezaobíde bez troch vecí: tácky s hranolkami, pohára kofoly a tabuľky čokolády. Každý účastník stretka má nejakú zásobu každej z týchto troch vecí. Tieto zásoby budeme reprezentovať prirodzenými číslami -- v prípade čokolády je to počet kociek, v prípade hranoliek je to počet hranoliek a v prípade kofoly je to počet MišoFových glgov.

MišoF popri bočných úmysloch (napríklad povedať niečo múdre) sleduje svoj primárny cieľ -- k jednej osobe si prisadnúť a zjesť jej všetky hranolky, všetku čokoládu a vypiť jej celú kofolu. Začal sa obzerať po ľuďoch a zisťovať, kto má koľko akej potraviny. MišoF je pre účely tejto úlohy parametrizovateľný troma reálnymi nezápornými hodnotami -- momentálnou chuťou na každú z potravín. Preto začal rátať takzvanú príjemnosť posedenia pre každého človeka. Príjemnosť posedenia s človekom je daná ako súčet hodnôt jeho potravín, pričom hodnota potraviny človeka je súčin jej množstva a MišoFovej chuti na danú potravinu. MišoF si vyberie človeka s najvyšším koeficientom príjemnosti posedenia.

Keď to ale MišoF všetko porátal, uvedomil si, že si chce z istých príčin sadnúť vedľa U$ámu. Nechce ale zradiť svoju oficiálnu a verejnú stratégiu výberu a preto sa rozhodol, že upraví svoje chute na potraviny. Pomôžte MišoFovi a nájdite hodnoty chutí na kofolu, hranolky a čokoládu tak, aby bol pre neho najvýhodnejší sused U$áma (prípadne zistite, že pri daných množstvách to nie je možné). Pomôžte mu rýchlo, pretože ináč U$áma stihne zjesť svoje hranolky a načo to potom bude dobré?

Úloha

Na vstupe je dané číslo . Nasleduje trojíc prirodzených čísel -- koľko majú jednotliví ľudia hranoliek, čokolády a kofoly. Prvá trojica sú U\$ámove hodnoty, 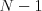zvyšných KSPákov nie je dôležité menovať. Čísla, ktoré vypíšete, nemusia byť celé (majú byť ale nezáporné).

Príklad

Vstup

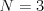
1 2 5
3 3 3
4 1 5

Výstup

1 4 5

Pri tomto ohodnotení bude mať U$áma hodnotu príjemnosti posedenia 34, zatiaľ čo ostatní dvaja KSPáci len 30, respektíve 33.

---

Účet