- KSP
- Séria
- Akcie
- Ostatné
- Iné semináre
/var/www/ksp-old/news/session_manager.php:30 with message SQLSTATE[HY000] [2002] Can't connect to local MySQL server through socket '/var/run/mysqld/mysqld.sock' (2)
Príklady druhého kola zimnej časti 28. ročníka KSP
Termín odoslania riešení tejto série je pondelok 10. januára 2011.
1. Zmiešaná postupnosť
10 bodov, kategória Z
Tánička veľmi rada triedi čísla. Lenže keď nemá čo triediť, tak sa nudí, a keď
sa nudí, vyžiera ostatným KSPákom desiatu. Keďže KSPáci sú veľmi neradi hladní,
tak sa rozhodli, že ju musia nejako zabaviť. Povedali si, že jej budú podhadzovať
postupnosti. Aby to malo efekt, potrebujú, aby dané postupnosti neboli
utriedené. Bohužiaľ, nemajú čas to kontrolovať (musia si strážiť desiatu),
a preto vás žiadajú o pomoc.
Úloha
Na prvom riadku vstupu je dané číslo  (dĺžka postupnosti,
(dĺžka postupnosti,  ) a na druhom nasleduje
postupnosť
) a na druhom nasleduje
postupnosť  navzájom rôznych čísel oddelených medzerou. Napíšte program,
navzájom rôznych čísel oddelených medzerou. Napíšte program,
ktorý túto postupnosť preusporiada a vypíše na výstup tak, aby nebola rastúca ani klesajúca.
Príklad
Vstup
5
1 2 3 4 7
Výstup
4 7 2 3 1
Vyhovuje ľubovoľné poradie okrem 1 2 3 4 7 a 7 4 3 2 1.
2. Zase tie závislosti
10 bodov, kategória Z
Tento príklad bude o Linuxe, balíčkoch a inštalovaní. Ak chceme v Linuxe
nainštalovať nejaký program, musíme nainštalovať balíček, ktorý ho
obsahuje. Avšak program potrebuje pre svoj beh napríklad knižnice. Každá
knižnica je v nejakom balíčku a preto potrebujeme mať nainštalované všetky
balíčky s knižnicami, ktoré potrebuje náš program. Tomuto hovoríme závislosť.
Ku každému balíčku v systéme poznáme zoznam balíčkov, na ktorých závisí. Tie však tiež potrebujú mať nainštalované nejaké ďalšie balíčky a tie ešte ďalšie balíčky (a takto by sme mohli pokračovať niekoľko strán).
Aby sme to nemali také ťažké, existujú rôzne pomocné programy. Povieme im zoznam balíčkov, ktoré chceme nainštalovať, a oni okrem nich nainštalujú aj všetky ostatné potrebné balíčky.
Najlepšie to demonštrujeme príkladom. Nech balíček 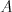 závisí na balíčku
závisí na balíčku 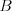 ,
,
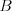 na
na 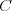 a
a 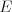 ,
, 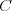 na
na 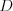 ,
, 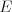 na
na 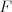 a
a 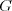 . Ak necháme nainštalovať balíček
. Ak necháme nainštalovať balíček 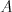 ,
tak sa nainštalujú aj balíčky
,
tak sa nainštalujú aj balíčky 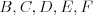 a
a 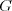 , lebo na nich priamo alebo nepriamo
závisí program
, lebo na nich priamo alebo nepriamo
závisí program 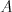 .
.
Niekedy potrebujeme "naklonovať" nainštalované balíčky na druhý počítač. Môžeme si spraviť zoznam všetkých balíčkov, ktoré sú nainštalované na prvom počítači, a presne tie nainštalovať na druhý počítač. Avšak ako vidno z príkladu vyššie, stačí nainštalovať iba niektoré balíčky a zvyšné sa doplnia automaticky.
Úloha
Prvý riadok vstupu obsahuje číslo  -- počet balíčkov, ktoré chceme nainštalovať.
Nasleduje
-- počet balíčkov, ktoré chceme nainštalovať.
Nasleduje  riadkov,
riadkov,  -ty z nich popisuje
-ty z nich popisuje  -ty balíček. Každý taký riadok
začína počtom balíčkov, na ktorých závisí balíček
-ty balíček. Každý taký riadok
začína počtom balíčkov, na ktorých závisí balíček  , a pokračuje ich zoznamom.
Všetky balíčky sú reprezentované celými číslami od
, a pokračuje ich zoznamom.
Všetky balíčky sú reprezentované celými číslami od 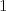 po
po  .
.
Vašou úlohou je napísať program, ktorý nájde a vypíše najmenšiu sadu balíčkov, ktorej nainštalovanie spôsobí nainštalovanie všetkých balíčkov.
Môžete predpokladať, že v závislostiach medzi balíčkami nie je cyklus a že
balíčkovací systém je korektný (každý balíček závisí len na existujúcich
balíčkoch). Cyklus v závislostiach je taká postupnosť balíčkov
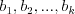 , že balíček
, že balíček 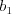 závisí na
závisí na 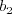 ,
, 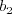 na
na 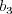 , ...,
, ..., 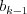 na
na
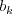 a
a 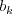 závisí na
závisí na 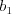 .
.
Príklad
Vstup
5
3 2 3 4
1 4
1 4
0
1 3
Výstup
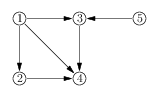
1 5
Takto vyzerajú závislosti balíčkov zo vstupu:
3. Zábudlivý dôchodca
10 bodov, kategória Z
V dobe krutej finančnej krízy sa snaží každá továreň minimalizovať svoje náklady na prevádzku,
preto sa prijímajú aj lacnejšie pracovné sily z radov dôchodcov, študentov a nelegálnych prisťahovalcov.
Inak tomu samozrejme nie je ani v továrni na triedenie čísiel. Preto keď prišla ponuka pána Michala, že
bude otročiť za jedlo, šaty a vzduch, bolo vedenie nadšené.
Rýchlo ale zistili, že to má drobný háčik. Pán Michal škúli, takže nikdy nevidí dve susedné čísla. To by ešte nebolo také hrozné, kebyže neprišiel pri absurdnej nehode s kapustou a zbíjačkou o krátkodobú pamäť. Takže príslovie ''zíde z očí, zíde z mysle'' preňho bohužiaľ platí doslovne.
Majiteľ však zistil, že keď nechá pána Michala triediť niektoré zákazky, napriek svojmu handicapu ich utriediť dokáže. Chcel by mať program, ktorý by mu pri zadaní zákazky povedal, či ju môže dať na starosť pánovi Michalovi. No a keď už je tá kríza, a vy ste študenti... môžete hádať.
Úloha
Na vstupe máte dané číslo  , v ďalšom riadku nasleduje
, v ďalšom riadku nasleduje  celých čísiel. Vašou úlohou je rozhodnúť,
či sme schopní získať z týchto čísiel neklesajúcu postupnosť, ak v jednom kroku môžeme
vymeniť iba dvojicu čísel na pozíciách
celých čísiel. Vašou úlohou je rozhodnúť,
či sme schopní získať z týchto čísiel neklesajúcu postupnosť, ak v jednom kroku môžeme
vymeniť iba dvojicu čísel na pozíciách 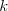 a
a  (
(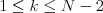 ).
).
Príklad
Vstup
5
10 45 52 14 37
Výstup
Ano.
Vymeníme najprv čísla na treťom a piatom mieste, potom tie na druhom a štvrtom mieste.
Príklad
Vstup
4
1 3 2 4
Výstup
Nie.
Výmenou prvého a tretieho, ani výmenou druhého a štvrtého čísla si veľmi nepomôžeme.
4. Zákerné kopce
Rytier Artur sa zúfalo pozerá pred seba. Ten svah, čo má pred nosom, sa mu vôbec, ale vôbec nepáči. Je strašne strmý -- keď sa na neho pokúša vyškriabať, vždy sa zošmykne späť dole. On sa ale naozaj potrebuje dostať na ten kopec. Hmm, že by to šlo nejak okolo?
Byť rytierom nie je žiadna slasť, také ťažké brnenie vám umožňuje
vyškrabať sa len na svah, ktorý na jednom yarde nestúpne o viac ako  stôp.
Našťastie je Artur statný a vysoký a vie nejaký ten jarok aj preskočiť,
pokiaľ nemá viac ako yard.
stôp.
Našťastie je Artur statný a vysoký a vie nejaký ten jarok aj preskočiť,
pokiaľ nemá viac ako yard.
Terén si môžeme zjednodušene predstaviť ako štvorcovú sieť s 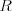 riadkami a
riadkami a 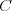 stĺpcami,
kde poznáme výšku každého políčka.
Artur sa vie hýbať na jeden krok/skok len v štvorci
stĺpcami,
kde poznáme výšku každého políčka.
Artur sa vie hýbať na jeden krok/skok len v štvorci 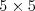 okolo seba (čiže jedným skokom vie každú
svoju súradnicu zmeniť maximálne o
okolo seba (čiže jedným skokom vie každú
svoju súradnicu zmeniť maximálne o 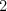 ).
Súčasne pri žiadnom kroku/skoku nemôže prekonať výškový rozdiel viac ako
).
Súčasne pri žiadnom kroku/skoku nemôže prekonať výškový rozdiel viac ako  .
Podarí sa mu nájsť cestu?
.
Podarí sa mu nájsť cestu?
Úloha
Prvý riadok vstupu obsahuje celé čísla 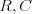 -- výšku a šírku mapy --
a celé číslo
-- výšku a šírku mapy --
a celé číslo  , ktoré určuje najväčší rozdiel (či už stúpanie alebo klesanie),
cez ktorý vie Artur v jednom kroku/skoku prejsť.
Druhý riadok obsahuje celé čísla
, ktoré určuje najväčší rozdiel (či už stúpanie alebo klesanie),
cez ktorý vie Artur v jednom kroku/skoku prejsť.
Druhý riadok obsahuje celé čísla 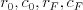 -- súradnice začiatočného
políčka
-- súradnice začiatočného
políčka 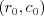 a koncového políčka
a koncového políčka 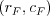 .
Ďalej nasleduje
.
Ďalej nasleduje 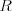 riadkov, v každom z nich sa nachádza
riadkov, v každom z nich sa nachádza 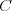 celých čísel --
výška daného políčka mapy.
celých čísel --
výška daného políčka mapy.
Pre rozmery mapy bude platiť 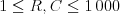 .
Ľavý horný roh mapy má súradnice
.
Ľavý horný roh mapy má súradnice 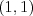 a pravý dolný roh zasa
a pravý dolný roh zasa 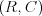 .
Súradnice začiatočného a koncového políčka budú vnútri mapy.
Výšky políčok a rovnako aj hodnota
.
Súradnice začiatočného a koncového políčka budú vnútri mapy.
Výšky políčok a rovnako aj hodnota  sú z rozsahu
sú z rozsahu ![[0, 10^9]](http://old.ksp.sk/wiki/pub/cache/db9ad969aabff8e2fd74edeba9009bb4.png) vrátane.
vrátane.
Vašou úlohou je vypísať dĺžku najkratšej cesty z políčka 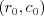 na
na 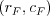 ,
alebo reťazec "
,
alebo reťazec "Artur, mas smolu." (bez úvodzoviek), ak cesta neexistuje.
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdáva jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v časovom limite.
Príklad
Vstup
10 10 3
1 1 10 10
2 0 0 0 0 0 0 0 0 0
0 0 0 8 0 0 0 0 0 0
0 5 0 0 0 0 0 0 0 0
0 0 0 0 0 6 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 4 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 7 0
0 0 0 0 0 0 0 0 500 2000
0 0 0 0 0 0 0 0 100 9
Výstup
6
Trasa vedie po políčkach s výškami 2, 5, 8, 6, 4, 7, 9. Všimnite si, že Artur nedoskočí z políčka s výškou 5 na políčko s výškou 6, lebo je ďaleko. Zároveň si všimnite, že Artura pri skoku zaujíma iba štartovacia a koncová výška, nie výška políčok medzitým.
5. Ošemetná situácia
Dominika si pri každom nákupe v blízkom hypermarkete kúpi pár škatúľ mlieka. Potom si ich pekne uloží do poličky. Naľavo tie, ktoré treba urýchlene spotrebovať, a napravo tie, ktoré ešte nejaký čas počkajú.
Žiaľ, po poslednej oslave nič neostalo na svojom mieste a mlieka sa záhadne pomiešali. Rada by ich dostala do pôvodného stavu, no nevie ako na to, pretože na intráku je málo miesta a nemôže ich všetky naraz vybrať von.
Úloha
Prvý riadok vstupu obsahuje jediné celé číslo  , ktoré označuje počet škatúľ mlieka v poličke.
Na druhom riadku je
, ktoré označuje počet škatúľ mlieka v poličke.
Na druhom riadku je  čísiel (každé z nich je buď
čísiel (každé z nich je buď 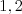 alebo
alebo 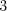 ) označujúcich trvanlivosť danej škatule.
) označujúcich trvanlivosť danej škatule.
Dominika môže naraz vymeniť len dve mlieka. Vypíšte takú postupnosť výmen, že po jej vykonaní budú škatule vo vzostupnom poradí podľa trvanlivosti.
Kvalita vášho algoritmu bude hodnotená podľa nasledovných kritérií (zoradené podľa dôležitosti):
- počet výmen (na toto sa pozeráme z pohľadu O-notácie, takže dva algoritmy, čo spravia napríklad
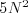 a
a 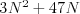 výmen, sú rovnako dobré),
výmen, sú rovnako dobré),
- časová zložitosť,
- pamäťová zložitosť.
Príklad
Vstup
3
3 3 2
Výstup
1 3
Vstup
4
2 3 2 1
Výstup
1 4
2 4
6. O švédskych stoloch
20 bodov, kategória O
Kde bolo, tam bolo, v škole v prírode bolo raz jedno sústredenie. Toto
sústredenie však bolo špeciálne --
nachádzali sa na ňom hory jedla umiestnené na švédskych stoloch.
Švédske stoly fungujú tak, že keď k stolu príde účastník sám, naloží si množstvo jedla ekvivalentné jeho hladu. Keď však príde k stolu ďalší účastník, tak rovnako ako aj pôvodný, rozhodne nechce zaostať a priloží si navyše. Keď príde viacero účastníkov, tiež nechce nikto hladovať, každý chce ostatných tromfnúť a tak si za každého priloží.
Hora jedla je však predsa len obmedzená, z čoho vyplýva, že vedúci musia riešiť závažný problém: kto dostane jedlo?
Úloha
Na vstupe je v prvom riadku počet účastníkov  a množstvo dostupného jedla
a množstvo dostupného jedla  . Nasleduje
. Nasleduje
 riadkov v tvare
riadkov v tvare  , kde
, kde 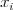 určuje množstvo jedla, ktoré skonzumuje
určuje množstvo jedla, ktoré skonzumuje
 -ty účastník a
-ty účastník a 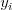 určuje množstvo jedla, ktoré
určuje množstvo jedla, ktoré  -ty účastník zje navyše
za každého ďalšieho účastníka pri stole. Ak teda vedúci
k stolu pustia
-ty účastník zje navyše
za každého ďalšieho účastníka pri stole. Ak teda vedúci
k stolu pustia 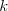 účastníkov,
účastníkov,  -ty účastník zje
-ty účastník zje 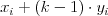 jedla. Napíšte
program, ktorý zistí, koľko najviac ľudí sa môže najesť.
jedla. Napíšte
program, ktorý zistí, koľko najviac ľudí sa môže najesť.
Príklad
Vstup
5 47
7 5
10 9
3 17
15 3
0 42
Výstup
2
Vedúci môžu pustiť k stolu napríklad prvého a tretieho účastníka.
7. Oktávy
20 bodov, kategória O
Halucinka robí rada na sústredkách budíčky gitarou. Otvorí si svoj spevník a začne spievať nejakú melódiu.
Tým zobudí Hermiho, ktorý sa chce hneď pridať. Avšak polorozospatý Hermi nezačne spievať presne to, čo Halucinka,
ale svoju melódiu. Halucinka rozmýšľa, či Hermi vlastne spieva tú istú pieseň. Pomôžte Halucinke zistiť,
či Hermi spieva v inej tónine, alebo je natoľko rozospatý, že spieva inú pieseň.
Úloha
Na vstupe dostanete popis dvoch melódií -- Halucinkinej a Hermiho. Každý popis začína číslom vyjadrujúcim počet tónov danej melódie, nasledujú jednotlivé tóny. Hermiho melódia je nanajvýš taká dlhá ako Halucinkina.
Halucinka aj Hermi majú rozsah 3 oktávy, dokážu preto zaspievať tieto tóny
(v poradí podľa výšky): C0, Cis0, D0, Dis0, E0,
F0, Fis0, G0, Gis0, A0, Ais0, H0,
C1, Cis1, D1, ..., Ais2, H2, C3.
Napíšte program, ktorý zistí, či si Hermi spieva tú istú pieseň ako Halucinka, teda či sa dá jeho melódia transponovať tak, aby vytvorila motív (čítaj podreťazec) Halucinkinej. Transponovať znamená každý tón Hermiho melódie posunúť o rovnaký počet poltónov (rovnakým smerom).
Riešenia, ktoré sa spoliehajú na generátor náhodných čísel a bez neho by
dosahovali horšiu časovú zložitosť, nemajú šancu získať plný počet bodov. Pri
výpočte časovej a pamäťovej zložitosti vášho algoritmu nezanedbávajte počet
tónov 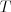 v Halucinkinom a Hermiho rozsahu ako konštantu (aj keď vieme, že
v Halucinkinom a Hermiho rozsahu ako konštantu (aj keď vieme, že
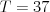 ).
).
Príklad
24 C1 D1 E1 F1 F1 F1 F1 E1 D1 E1 E1 E1 E1 D1 C1 D1 D1 D1 D1 E1 D1 C1 C1 C1 12 H0 Ais0 Gis0 Ais0 Ais0 Ais0 Ais0 Gis0 Fis0 Gis0 Gis0 Gis0
Výstup
Ano
Halucinka si spieva Kohútika jarabého a Hermi tiež, na vstupe je zachytený jeho prostriedok. Celý Hermiho Kohútik jarabí (posunutý o 6 poltónov nižšie) znie: Fis0 Gis0 Ais0 H0 H0 H0 H0 Ais0 Gis0 Ais0 Ais0 Ais0 Ais0 Gis0 Fis0 Gis0 Gis0 Gis0 Gis0 Ais0 Gis0 Fis0 Fis0 Fis0.
Príklad
20
C1 D1 E1 F1 G1 F1 F1 F1 D1 C1 C1 D1 E1 F1 G1 F1 F1 F1 D1 C1
12
A1 H1 Cis2 Cis2 H1 A1 E2 E2 Fis2 E2 H1 H1
Výstup
Nie
Halucinka si spieva Na zelenej lúke sedí zajac a Hermi si spieva Pod horou, pod horou.
8. Obedy sa vydávajú do siedmej
25 bodov, kategórie O a T
Na intrákoch prednedávnom otvorili novú Novú jedáleň. Aby prežila v tvrdej
konkurencii, pripravujú v nej pomocou moderných technológií jedlo na mieru.
Najprv každý študent podstúpil síce nepríjemnú, ale zato povinnú analýzu svojich
chuťových buniek; na základe jej výsledkov mu potom priradili jedinečný pokrm.
Po prekonaní prvotnej nedôvery ale študenti zistili, že obedy na mieru sú naozaj
vynikajúce a čakať v rade na ne sa oplatí.
Všetko jedlo pripravuje automatizovaná výrobná linka, na ktorej konci stojí
zamestnankyňa jedálne (študentmi nesprávne označovaná ako teta kuchárka)
a vydáva obedy. Výrobná linka je však automatizovaná až príliš. Každé ráno si
sama vymyslí a vytlačí zoznam  jedál, ktoré v ten deň pripraví presne
v poradí, v akom sa nachádzajú na zozname (jedlá na ňom sa môžu aj opakovať).
jedál, ktoré v ten deň pripraví presne
v poradí, v akom sa nachádzajú na zozname (jedlá na ňom sa môžu aj opakovať).
Teta kuchárka sa smutne pozerá na dnešný rad  študentov, ktorí čakajú na
obed. Ich poradie sa totiž podstatne líši od zoznamu jedál, ktorý na dnes
vytlačila výrobná linka. No a pretože študenti odmietajú jesť obed pripravený
pre niekoho iného, často stojí teta kuchárka pred dilemou: vyhodiť porciu alebo
študenta?
študentov, ktorí čakajú na
obed. Ich poradie sa totiž podstatne líši od zoznamu jedál, ktorý na dnes
vytlačila výrobná linka. No a pretože študenti odmietajú jesť obed pripravený
pre niekoho iného, často stojí teta kuchárka pred dilemou: vyhodiť porciu alebo
študenta?
Pomôžte tete kuchárke a nájdite postup, ktorý zaručí, že sa naobeduje čo najviac študentov.
Úloha
V prvom riadku vstupu sú zadané čísla  a
a  (
(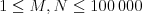 ).
Druhý riadok reprezentuje rad študentov: čísla
).
Druhý riadok reprezentuje rad študentov: čísla 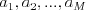 . Tretí
riadok zase obsahuje zoznam jedál, ktoré dnes pripraví výrobná linka: čísla
. Tretí
riadok zase obsahuje zoznam jedál, ktoré dnes pripraví výrobná linka: čísla
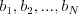 . Platí
. Platí 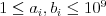 . V rade študentov sa
žiadne číslo neopakuje. Všetky čísla na riadku sú oddelené jednou medzerou.
. V rade študentov sa
žiadne číslo neopakuje. Všetky čísla na riadku sú oddelené jednou medzerou.
Nájdite a na jediný riadok výstupu vypíšte najväčšie také číslo  , že sa zo
zoznamu jedál aj z radu študentov dá vyškrtať niekoľko vhodných čísel tak, aby
nám zostali dve rovnaké postupnosti dĺžky
, že sa zo
zoznamu jedál aj z radu študentov dá vyškrtať niekoľko vhodných čísel tak, aby
nám zostali dve rovnaké postupnosti dĺžky  (tí študenti, ktorí dnes dostanú
svoju porciu).
(tí študenti, ktorí dnes dostanú
svoju porciu).
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdáva jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v časovom limite.
Príklad
Vstup
5 8
7 3 4 8 1
2 2 3 9 1 8 4 1
Výstup
3
Naobedujú sa študenti 3, 4, 1 alebo 3, 8, 1.
9. Tesnotka pred kontrolou
25 bodov, kategória T
Po neúspechu s predajom slúchadiel sa Bob rozhodol, že si otvorí kníhkupectvo.
Doba je ale ťažká a tak sa rozhodol, že popri predaji legálnej literatúry si bude privyrábať aj
predajom tej ilegálnej, zaoberajúcej sa programovaním.
Čo čert nechcel, kontrola z EÚ sa rozhodla navštíviť Bobovo kníhkupectvo. Keď to zistil, mal práve v obchode párny počet ilegálnych kníh a dvoch zákazníkov, ktorí boli zaujatí týmto tovarom. Rozhodol sa, že využije túto príležitosť, zbaví sa kníh a rozdelí im ich rovným dielom. Každý zákazník si po kúpe spočíta, koľko v priemere zaplatil za jednu samohlásku (to je predsa to, čo nás v tejto literatúre zaujíma). Bob chce kvôli budovaniu dobrého mena firmy dosiahnuť, aby bol súčet týchto dvoch hodnôt čo najmenší.
Úloha
Prvý riadok vstupu obsahuje párne číslo  (
(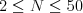 ).
Druhý riadok obsahuje
).
Druhý riadok obsahuje  medzerou oddelených čísel, pričom
medzerou oddelených čísel, pričom 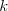 -te číslo vyjadruje počet samohlások
v
-te číslo vyjadruje počet samohlások
v 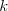 -tej knihe.
Tretí riadok obsahuje
-tej knihe.
Tretí riadok obsahuje  medzerou oddelených čísel, pričom
medzerou oddelených čísel, pričom 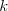 -te z nich zasa vyjadruje cenu
-te z nich zasa vyjadruje cenu 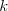 -tej knihy.
Počty samohlások aj ceny kníh sú celé čísla z rozsahu
-tej knihy.
Počty samohlások aj ceny kníh sú celé čísla z rozsahu ![[1, 500]](http://old.ksp.sk/wiki/pub/cache/d85ae72664b105f4eb2701b74b17d706.png) (vrátane).
(vrátane).
Vašou úlohou je rozdeliť tieto knihy na dve kopy tak, aby v každej kope bolo 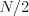 kníh a keď spočítame
priemernú cenu za samohlásku v každej kope, tak súčet týchto dvoch hodnôt bude čo najmenší.
kníh a keď spočítame
priemernú cenu za samohlásku v každej kope, tak súčet týchto dvoch hodnôt bude čo najmenší.
Na výstup vypíšte jedno číslo: najmenší možný dosiahnuteľný súčet priemerných cien. Vypíšte aspoň 10
desatinných miest. Vaša odpoveď by mala mať absolútnu alebo relatívnu chybu najviac 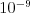 .
.
Odovzdávanie:
Tento príklad je praktický, čo znamená, že sa dá odovzdáva jedine elektronicky, pričom stačí odovzdať iba zdrojový kód. Pri odovzdaní sa vám program otestuje na niekoľkých vstupoch a dostane body podľa toho, na koľkých vstupoch dá správny výsledok v časovom limite.
Príklad
Vstup
2
2 4
3 4
Výstup
2.5
Vstup
4
1 1 2 2
1 1 1 1
Výstup
1.3333333333
Každému zákazníkovi Bob predá knihu s jednou a s dvoma samohláskami.
10. Turbulencia a krevety
25 bodov, kategória T
Tomi a Jano sedia v lietadle. Let je dlhý a preto je jeho súčasťou aj obed.
Letecká spoločnosť pridala k obedu špeciálny bonus -- originál krevety
v plastovom tégliku. Väčšina cestujúcich si ich len nedôverčivo
obzrela, ale niektorí odvážlivci sa rozhodli vyskúšať túto novotu. Lenže chvíľu nato prišla
silná turbulencia, viaceré žalúdky spravili piruetu a patriční odvážlivci
okrevetili celé svoje široké okolie.
Právnici letovej spoločnosti zistili, že nie sú viazaní preplácať škodu všetkým -- stačí, keď ako symbolické gesto vynahradia škodu tomu, kto je na tom najhoršie, aby nevyzerali zle v novinách.
Tzv. najväčší chudák je človek, ktorého zasiahlo svojimi krevetami najviac ľudí, ale pritom si sám krevety nedal a teda za nič nemôže. Vašou úlohou je zistiť, kto to je a koľko cestujúcich ho zasiahlo (lebo od toho potom záleží, koľko mu treba zaplatiť).
Úloha
Lietadlo je dlhé 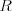 radov a každý rad je široký
radov a každý rad je široký 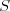 sedadiel. Na každom
sedadle sedí jeden cestujúci.
sedadiel. Na každom
sedadle sedí jeden cestujúci.  cestujúcich si dalo krevety a potom
okrevetili svojich okolosediacich -- konkrétne štvorec so stranou
cestujúcich si dalo krevety a potom
okrevetili svojich okolosediacich -- konkrétne štvorec so stranou 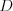 ,
v strede ktorého sú. (
,
v strede ktorého sú. (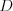 je nepárne číslo.)
je nepárne číslo.)
Na vstupe sú prirodzené čísla 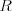 ,
, 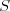 ,
,  a
a 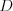 ; ďalej
; ďalej  riadkov so
súradnicami jednotlivých odvážlivcov (súradnice sú v poradí rad, sedadlo;
čísluje sa od 1). Aspoň jeden cestujúci si
krevety nedal. Váš program má vypísať jedno číslo -- koľko ľudí zasiahlo najväčšieho chudáka.
riadkov so
súradnicami jednotlivých odvážlivcov (súradnice sú v poradí rad, sedadlo;
čísluje sa od 1). Aspoň jeden cestujúci si
krevety nedal. Váš program má vypísať jedno číslo -- koľko ľudí zasiahlo najväčšieho chudáka.
Lietadlo je interkontinentálne a teda strašne veľké.
Zložitosť vášho programu nesmie závisieť od 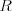 a
a 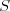 , lebo to bude
trvať večnosť a leteckú spoločnosť medzitým všetci novinári roznesú v zuboch.
, lebo to bude
trvať večnosť a leteckú spoločnosť medzitým všetci novinári roznesú v zuboch.
Príklad
Vstup
6 5 3 5
2 1
4 3
6 5
Výstup
2
Cestujúceho na sedadle (4, 3) síce okrevetili traja, ale keďže si sám dal krevety, nemôže to byť najväčší chudák.
Posledná úprava 06 január, 2011, 16:27 CET, túto podstránku generuje pmWiki

